Исследование точности численного интегрирования
Отчет по курсовой работе дисциплины «Информатика»
Студент Лаптев С.
гр. Р-200802 ________________ ______________
дата сдачи работы Подпись
Преподаватель _________________ _______________ Плохих О.В.
дата приема работы Подпись
Екатеринбург
Оглавление
1. Задание исследования. 3
2. Подробное описание задачи и способы ее решения. 3
Метод трапеций. 3
Метод Симпсона. 3
3. Результаты исследований. 4
3.1. Сравнение результатов. 19
4. Выводы.. 20
5. Приложение. 21
5.1. Описание применения. 21
5.1.1. Назначение программы.. 21
5.1.2. Условия применения. 21
5.1.3. Описание значения. 21
5.2. Программа и методика испытаний. 22
5.2.1. Объект испытаний. 22
5.2.2. Цель испытаний. 22
5.2.3. Требования к программе. 22
5.2.4. Требования к программной документации. 22
5.2.5. Средства и порядок испытаний. 22
5.2.6. Метод испытаний. 22
5.3. Руководство пользователя. 25
5.3.1. Назначение программы.. 25
5.3.2. Условия и характеристики программы.. 25
5.3.3. Выполнение программы.. 25
5.3.4. Сообщения программы.. 25
5.3.5. Входные и выходные данные. 25
5.3.6. Сборка программы.. 25
5.4. Описание программы.. 26
5.4.1. Общие сведения. 26
5.4.2. Функциональное назначение. 26
5.4.3. Описание логической структуры.. 26
5.4.4. Используемые технические средства. 27
5.4.5. Вызов и загрузка. 27
5.4.6. Входные и выходные данные. 27
5.5. Текст программы.. 28
Задание исследования
Провести исследование внутренней сходимости численного интегрирования методом Симпсона и трапеций различных функций, задаваемых с помощью языка С++.
Подробное описание задачи и способы ее решения
Необходимо провести исследования так называемой внутренней сходимости численного интегрирования методами трапеций и Симпсона различных функций, задаваемых с помощью функций языка С++. Предполагается, что отрезок интегрирования [a,b] разбит на n равных частей системой точек (сеткой).
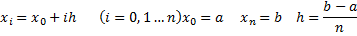
Контроль внутренней сходимости заключается в циклическом вычислении приближенных значений интеграла для удваимого по сравнению со значением на предыдущем прохождении цикла числа n. Отношения абсолютной величины разности этих значений к абсолютной величине предыдущего приближенного значения принимается в качестве критерия достижения точности интеграла.
Построить зависимости количеств итераций от различных величин критерия точности.
Построить обратные зависимости критерия точности от количества итераций.
Повторить все вышеуказанные исследования для случая, когда при вычислении критерия точности разность значений интеграла относится не к предыдущему значению, а к точному значению аналитически вычисленного интеграла.
Исследовать влияние увеличения верхнего предела интегрирования на точность (при прочих неизменных условиях).
Метод трапеций

Метод Симпсона

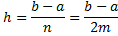
Результаты исследований
Таблицы и графики зависимостей количества итераций от различных величин критерия точности для интегралов, вычисленных методом трапеций:
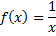
| Критерийточности | Количествоитераций |
| 0,0001642 | |
| 0,0000554 | |
| 0,0000199 | |
| 0,0000097 | |
| 0,000003 | |
| 0,0000024 | |
| 0,000021 | |
| 0,0001352 | |
| 0,0004427 | |
| 0,0017771 | |
| 0,0070933 | |
| 0,0733414 | |
| 0,1639168 | |
| 0,1591954 |

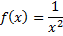
| Критерийточности | Количествоитераций |
| 0,0000435 | |
| 0,0000246 | |
| 0,0000098 | |
| 0,0000027 | |
| 0,0000054 | |
| 0,0000034 | |
| 0,0000111 | |
| 0,0000371 | |
| 0,0003384 | |
| 0,0005241 | |
| 0,0024769 | |
| 0,0193195 | |
| 0,0460816 | |
| 0,0891634 | |
| 0,1816833 |

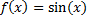
| Критерийточности | Количествоитераций |
| 0,0000009 | |
| 0,0000005 | |
| 0,000001 | |
| 0,0000016 | |
| 0,0000005 | |
| 0,000001 | |
| 0,0000223 | |
| 0,000056 | |
| 0,0003561 | |
| 0,0002782 | |
| 0,0003474 | |
| 0,0066709 | |
| 0,0042367 | |
| 0,0053266 | |
| 0,0052932 |


| Критерийточности | Количество итераций |
| 0,7210944 | |
| 5,7138805 | |
| 0,5115891 | |
| 0,1587429 | |
| 0,2640994 | |
| 0,273518 | |
| 0,7462801 | |
| 0,1349342 | |
| 0,1746383 | |
| 0,322107 | |
| 61,4329529 | |
| 1,0215764 | |
| 0,0930657 | |
| 0,0566663 | |
| 0,0027258 |


| Критерийточности | Количествоитераций |
| 0,0000017 | |
| 0,0000075 | |
| 0,000004 | |
| 0,0000028 | |
| 0,0000031 | |
| 0,0000033 | |
| 0,0000019 | |
| 0,0000064 | |
| 0,0000001 | |
| 0,0000386 | |
| 0,0000803 | |
| 0,0007838 | |
| 0,0016693 | |
| 0,0005451 | |
| 0,0119303 |


| Критерийточности | Количествоитераций |
| 0,0000001 | |
| 0,0000118 | |
| 0,0000105 | |
| 0,0000047 | |
| 0,000003 | |
| 0,0000023 | |
| 0,0000019 | |
| 0,0000048 | |
| 0,0000013 | |
| 0,0000021 | |
| 0,0000579 | |
| 0,0001056 | |
| 0,0012424 | |
| 0,0027928 | |
| 0,0026273 |

Таблицы и графики зависимостей количества итераций от различных значений критерия точности для интегралов, вычисленных методом Симпсона:
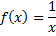
| Критерийточности | Количествоитераций |
| 0,0000366 | |
| 0,0000148 | |
| 0,0000097 | |
| 0,0000029 | |
| 0,000005 | |
| 0,0000158 | |
| 0,0000078 | |
| 0,0001184 | |
| 0,000019 | |
| 0,000466 | |
| 0,0069997 | |
| 0,0210596 | |
| 0,0596227 | |
| 0,0416028 | |
| 0,1333978 |

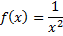
| Критерийточности | Количествоитераций |
| 0,0000529 | |
| 0,0000309 | |
| 0,0000055 | |
| 0,0000206 | |
| 0,0000275 | |
| 0,0000172 | |
| 0,0000026 | |
| 0,0000373 | |
| 0,0001679 | |
| 0,0009911 | |
| 0,001429 | |
| 0,0012871 | |
| 0,0251969 | |
| 0,0904129 | |
| 0,1624286 |
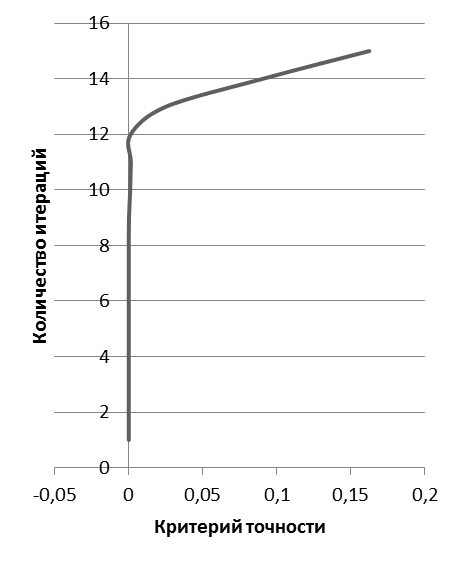
| Критерийточности | Количествоитераций |
| 0,0002614 | |
| 0,0001696 | |
| 0,0000683 | |
| 0,0000173 | |
| 0,000005 | |
| 0,0000016 | |
| 0,0000146 | |
| 0,0000081 | |
| 0,0000532 | |
| 0,0001906 | |
| 0,0000148 | |
| 0,0016623 | |
| 0,0047355 | |
| 0,0001972 | |
| 0,0441604 |


| Критерийточности | Количество итераций |
| 1,3475398 | |
| 299,5162048 | |
| 0,6511438 | |
| 0,769284 | |
| 0,831215 | |
| 1,4512321 | |
| 0,2898597 | |
| 0,4690856 | |
| 0,1021232 | |
| 0,0488429 | |
| 0,2428324 | |
| 0,3262224 | |
| 0,0297503 | |
| 0,0498698 | |
| 0,0221329 |


| Критерийточности | Количествоитераций |
| 0,001854 | |
| 0,0011909 | |
| 0,0008299 | |
| 0,0000531 | |
| 0,0001553 | |
| 0,0000502 | |
| 0,0000104 | |
| 0,0000078 | |
| 0,0000058 | |
| 0,000028 | |
| 0,0000372 | |
| 0,0001925 | |
| 0,0004425 | |
| 0,0016719 | |
| 0,0065919 |


| Критерийточности | Количествоитераций |
| 0,0023198 | |
| 0,0015105 | |
| 0,0010463 | |
| 0,0005129 | |
| 0,0001719 | |
| 0,0000787 | |
| 0,0000228 | |
| 0,0000053 | |
| 0,0000017 | |
| 0,0000023 | |
| 0,0000167 | |
| 0,000088 | |
| 0,0000317 | |
| 0,0013675 | |
| 0,0006897 |
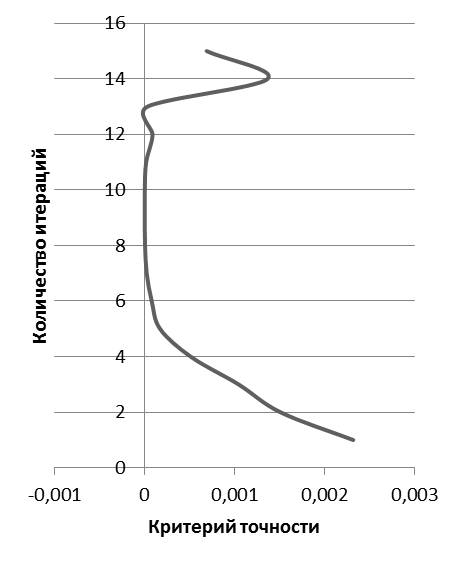
Обратные зависимости критерия точности от количества итераций:
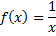

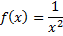

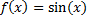







Сравнительная таблица значений критерия,полученных по отношению к предыдущему значению и по отношению к аналитическому значению для интеграла, вычисленного методом трапеций:
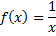
| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,0001642 | 0,0000916 | ||
| 0,0000554 | 0,0000361 | ||
| 0,0000199 | 0,0000162 | ||
| 0,0000097 | 0,0000065 | ||
| 0,000003 | 0,0000035 | ||
| 0,0000024 | 0,0000059 | ||
| 0,000021 | 0,000015 | ||
| 0,0001352 | 0,0001503 | ||
| 0,0004427 | 0,0005929 | ||
| 0,0017771 | 0,0023689 | ||
| 0,0070933 | 0,0094454 | ||
| 0,0733414 | 0,0632033 | ||
| 0,1639168 | 0,1110735 | ||
| 0,1110735 | |||
| 0,1591954 | 0,2525865 |
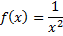
| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,0000435 | 0,0000444 | ||
| 0,0000246 | 0,0000198 | ||
| 0,0000098 | 0,00001 | ||
| 0,0000027 | 0,0000073 | ||
| 0,0000054 | 0,0000019 | ||
| 0,0000034 | 0,0000053 | ||
| 0,0000111 | 0,0000058 | ||
| 0,0000371 | 0,0000428 | ||
| 0,0003384 | 0,0002955 | ||
| 0,0005241 | 0,0002287 | ||
| 0,0024769 | 0,002705 | ||
| 0,0193195 | 0,0165622 | ||
| 0,0460816 | 0,0302826 | ||
| 0,0891634 | 0,1167459 | ||
| 0,1816833 | 0,2772185 |
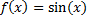
| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,0000009 | 0,0000002 | ||
| 0,0000005 | 0,0000007 | ||
| 0,000001 | 0,0000002 | ||
| 0,0000016 | 0,0000018 | ||
| 0,0000005 | 0,0000014 | ||
| 0,000001 | 0,0000004 | ||
| 0,0000223 | 0,0000219 | ||
| 0,000056 | 0,000078 | ||
| 0,0003561 | 0,0002781 | ||
| 0,0002782 | |||
| 0,0003474 | 0,0003474 | ||
| 0,0066709 | 0,0063258 | ||
| 0,0042367 | 0,0105358 | ||
| 0,0053266 | 0,0052653 | ||
| 0,0052932 |

| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,7210944 | Не определен | ||
| 5,7138805 | Не определен | ||
| 0,5115891 | Не определен | ||
| 0,1587429 | Не определен | ||
| 0,2640994 | Не определен | ||
| 0,273518 | Не определен | ||
| 0,7462801 | Не определен | ||
| 0,1349342 | Не определен | ||
| 0,1746383 | Не определен | ||
| 0,322107 | Не определен | ||
| 61,4329529 | Не определен | ||
| 1,0215764 | Не определен | ||
| 0,0930657 | Не определен | ||
| 0,0566663 | Не определен | ||
| 0,0027258 | Не определен |

| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,0000017 | 0,0000106 | ||
| 0,0000075 | 0,0000181 | ||
| 0,000004 | 0,0000221 | ||
| 0,0000028 | 0,0000249 | ||
| 0,0000031 | 0,0000281 | ||
| 0,0000033 | 0,0000314 | ||
| 0,0000019 | 0,0000333 | ||
| 0,0000064 | 0,0000269 | ||
| 0,0000001 | 0,000027 | ||
| 0,0000386 | 0,0000116 | ||
| 0,0000803 | 0,0000919 | ||
| 0,0007838 | 0,000692 | ||
| 0,0016693 | 0,0009761 | ||
| 0,0005451 | 0,0015218 | ||
| 0,0119303 | 0,0104267 |

| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,0000001 | 0,0000172 | ||
| 0,0000118 | 0,000029 | ||
| 0,0000105 | 0,0000395 | ||
| 0,0000047 | 0,0000442 | ||
| 0,000003 | 0,0000471 | ||
| 0,0000023 | 0,0000494 | ||
| 0,0000019 | 0,0000475 | ||
| 0,0000048 | 0,0000522 | ||
| 0,0000013 | 0,000051 | ||
| 0,0000021 | 0,0000488 | ||
| 0,0000579 | 0,0000091 | ||
| 0,0001056 | 0,0001147 | ||
| 0,0012424 | 0,0011278 | ||
| 0,0027928 | 0,0016618 | ||
| 0,0026273 | 0,0009698 |
Сравнительная таблица значений критерия,полученных по отношению к предыдущему значению и по отношению к аналитическому значению для интеграла, вычисленного методом Симпсона:
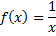
| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,0000366 | 0,0000367 | ||
| 0,0000148 | 0,0000515 | ||
| 0,0000097 | 0,0000612 | ||
| 0,0000029 | 0,0000584 | ||
| 0,000005 | 0,0000534 | ||
| 0,0000158 | 0,0000376 | ||
| 0,0000078 | 0,0000298 | ||
| 0,0001184 | 0,0000886 | ||
| 0,000019 | 0,0000696 | ||
| 0,000466 | 0,0005357 | ||
| 0,0069997 | 0,0075391 | ||
| 0,0210596 | 0,0136792 | ||
| 0,0596227 | 0,0724863 | ||
| 0,0416028 | 0,1110735 | ||
| 0,1333978 | 0,2296544 |
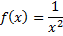
| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,0000529 | 0,0000535 | ||
| 0,0000309 | 0,0000844 | ||
| 0,0000055 | 0,0000899 | ||
| 0,0000206 | 0,0000693 | ||
| 0,0000275 | 0,0000418 | ||
| 0,0000172 | 0,0000246 | ||
| 0,0000026 | 0,000022 | ||
| 0,0000373 | 0,0000593 | ||
| 0,0001679 | 0,0002272 | ||
| 0,0009911 | 0,0007638 | ||
| 0,001429 | 0,0021938 | ||
| 0,0012871 | 0,0009039 | ||
| 0,0251969 | 0,0243158 | ||
| 0,0904129 | 0,1125302 | ||
| 0,1624286 | 0,2566807 |
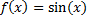
| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,0002614 | 0,0002623 | ||
| 0,0001696 | 0,0000927 | ||
| 0,0000683 | 0,0000245 | ||
| 0,0000173 | 0,0000072 | ||
| 0,000005 | 0,0000022 | ||
| 0,0000016 | 0,0000038 | ||
| 0,0000146 | 0,0000184 | ||
| 0,0000081 | 0,0000103 | ||
| 0,0000532 | 0,0000635 | ||
| 0,0001906 | 0,0002541 | ||
| 0,0000148 | 0,0002393 | ||
| 0,0016623 | 0,0019011 | ||
| 0,0047355 | 0,0066277 | ||
| 0,0001972 | 0,0064318 | ||
| 0,0441604 | 0,0503082 |

| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 1,3475398 | Не определен | ||
| 299,5162048 | Не определен | ||
| 0,6511438 | Не определен | ||
| 0,769284 | Не определен | ||
| 0,831215 | Не определен | ||
| 1,4512321 | Не определен | ||
| 0,2898597 | Не определен | ||
| 0,4690856 | Не определен | ||
| 0,1021232 | Не определен | ||
| 0,0488429 | Не определен | ||
| 0,2428324 | Не определен | ||
| 0,3262224 | Не определен | ||
| 0,0297503 | Не определен | ||
| 0,0498698 | Не определен | ||
| 0,0221329 | Не определен |

| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,001854 | 0,0018223 | ||
| 0,0011909 | 0,0006292 | ||
| 0,0008299 | 0,0002012 | ||
| 0,0000531 | 0,0002543 | ||
| 0,0001553 | 0,0000991 | ||
| 0,0000502 | 0,0000489 | ||
| 0,0000104 | 0,0000385 | ||
| 0,0000078 | 0,0000307 | ||
| 0,0000058 | 0,0000365 | ||
| 0,000028 | 0,0000645 | ||
| 0,0000372 | 0,0000272 | ||
| 0,0001925 | 0,0002197 | ||
| 0,0004425 | 0,000662 | ||
| 0,0016719 | 0,0010088 | ||
| 0,0065919 | 0,0055898 |

| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерийточности | Количествоитераций | Критерийточности | Количествоитераций |
| 0,0023198 | 0,0023715 | ||
| 0,0015105 | 0,0008646 | ||
| 0,0010463 | 0,0001808 | ||
| 0,0005129 | 0,0003322 | ||
| 0,0001719 | 0,0001603 | ||
| 0,0000787 | 0,0000817 | ||
| 0,0000228 | 0,0000589 | ||
| 0,0000053 | 0,0000536 | ||
| 0,0000017 | 0,0000518 | ||
| 0,0000023 | 0,0000541 | ||
| 0,0000167 | 0,0000708 | ||
| 0,000088 | 0,0000172 | ||
| 0,0000317 | 0,0000146 | ||
| 0,0013675 | 0,001382 | ||
| 0,0006897 | 0,0020707 |
Сравнениерезультатов
Таблица сравнительных результатов:
| Методтрапеций n=1000 | МетодСимпсона n =1000 | Аналитический результат | Функция | Пределы |
| 4,5002217 | 4,4996448 | 4,4998096 | f(x)=1/x | 0,1…..9 |
| 1,6667408 | 1,6665776 | 1,6666667 | f(x)=1/x*x | 0,5…..3 |
| 1,9999987 | 1,9999982 | f(x)=sin(x) | 0…….π | |
| -0,0000007 | -0,0000009 | f(x)=sin(2*x) | 0…….π | |
| 0,2857112 | 0,2862349 | 0,2857142 | f(x)=sin(7*x) | 0…....π |
| 0,2222184 | 0,2216952 | 0,2222222 | f(x)=sin(9*x) | 0…....π |
Таблица влияния увеличения верхнего предела на точность интегрирования на примере функции:
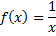
| Аналитическое значение | Практическое значение | Верхний предел | Погрешность |
| 4,4998097 | 4,5002217 | 0,000412 | |
| 4,6051701 | 4,6056180 | -0,0004479 | |
| 4,7874917 | 4,7880392 | -0,0005475 | |
| 4,9416424 | 4,9422879 | -0,0006455 | |
| 5,0751738 | 5,0759511 | -0,0007773 | |
| 5,1929568 | 5,1938734 | -0,0009166 | |
| 5,2983173 | 5,2993822 | -0,0010649 |
Таб. 2 - Таблица влияния увеличения верхнего предела на точность интегрирования
Из таблицы видно, что увеличение верхнего предела приводит к уменьшению точности интегрирования.
Выводы
В ходе выполнения данной работы было выявлено, что при увеличении количества разбиений отрезков интегрирования значения, полученные численными методами, стремятся к аналитически вычисленному значению интеграла.
Критерии точности относительно предыдущего вычисления и относительно аналитически вычисленного примерно равны, это означает, что численные методы являются достаточно точными. Но метод трапеций является более точным методом вычисления значения интеграла, чем метод Симпсона. При его вычислениях были замечены наименьшие неточности вычисления.
Также было выявлено, что при увеличении значения верхнего предела интегрирования любым из предложенных методов, критерий точности интегрирования становится больше. Следовательно, увеличение верхнего предела приводит к уменьшению точности интегрирования.
Приложение
Описание применения
Назначение программы
Программа lap предназначена для исследования точности численного интегрирования методами трапеций и Симпсона для степенных функций и функций вида sin(mx).
Программа применяется для вычисления погрешностей численного интегрирования, нахождения значения интеграла методами трапеций и Симпсона и вычисления критерия точности. Результаты вычисления записываются в файл data.xls (при отсутствии данного файла программа запрашивает ввести имя файла с клавиатуры), предназначенный для работы в программном продукте MicrosoftExcel 2007. Построение графиков зависимостей критерия точности от количества итерацийпроизводятся также с помощью Excel 2007.
Условия применения
Для выполнения программы достаточно вычислительной установки типа PC с процессором PentiumIII (или быстрее) и 128 Мбайт оперативной памяти, оснащенной любой из следующих операционных систем: MicrosoftWindowsNT и выше.
Описание значения
Вычисления точности численного интегрирования методов трапеций и Симпсона сводится к сравнению соседних значений интегралов, а также сравнению значений с аналитическим значением интеграла.
Программа и методика испытаний
Объект испытаний
Объектом испытаний является исполняемый модуль программы lap. Программа lap предназначена для исследования точности численного интегрирования методами трапеций и Симпсона для степенных функций и функций вида sin(mx).
Цель испытаний
Целью испытаний является проверка точности работы программы на конкретной вычислительной установке.
Требования к программе
Во время испытаний следует проверить правильное прохождение контрольного примера при решении задачи двумя различными методами.






