Задания для самостоятельной работы 16-17 февраля 2017г.
1. Осевое сечение цилиндра – квадрат, длина диагонали которого 36 см,
Найдите радиус основания цилиндра, площадь основания, площадь боковой поверхности и объем цилиндра.
2. Высота конуса равна 15 см, радиус основания 8 см. Найдите образующую конуса, площадь боковой поверхности и объем конуса.
3. Шар радиусом 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найдите площадь сечения, площадь поверхности и объем шара.
4. Высота конуса равна  см, а угол при вершине осевого сечения
см, а угол при вершине осевого сечения  .
.
Найдите площадь полной поверхности и объем конуса.
5. В шаре радиуса 15см проведено сечение, площадь которого равна 81см2. Найдите объём меньшего шарового сегмента, отсекаемого плоскостью сечения.
Задания для самостоятельной работы 20-21 февраля 2017г.
1. Посмотреть Презентацию «Задание 20 база» (ссылка: https://vk.com/math_noc).
2. Решить задачи в тетради:
1) Воробей прыгает вдоль прямой в любом направлении. Длина прыжка равна единичному отрезку. Сколько существует точек, в которых воробей может оказаться, сделав 5 прыжков?
2) Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 1 м. Высота дерева 13 м. За сколько дней улитка впервые доползёт до вершины дерева?
3) В бак объёмом 38 литров каждый час, начиная с 12 часов, наливают полное ведро воды объёмом 8 литров. Но в днище бака есть небольшая щель, и из неё за час вытекает 3 литра. В какой момент времени (в часах) бак будет заполнен полностью.
4) Саша пригласил Петю в гости, сказав, что живёт в двенадцатом подъезде в квартире № 465, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом пятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
5) Катя с подружкой Леной пошли в гости к Свете, зная, что она живёт в 364-й квартире в 6-ом подъезде. Подойдя к дому, они обнаружили, что дом 16-тиэтажный. На каком этаже живёт Света? (На всех этажах число квартир одинаковое, номера квартир начинаются с единицы).
6) Во всех подъездах дома одинаковое число этажей, а на каждом этаже одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 170 квартир?
7) В обменном пункте можно совершить одну из двух операций:
1) за 4 золотых монеты получить 6 серебряных и одну медную;
2) за 10 серебряных монет получить 5 золотых и одну медную.
8) У Саши были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 45 медных. На сколько уменьшилось количество серебряных монет у Саши?
9) Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
10) В корзине лежат 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов хотя бы один груздь. Сколько рыжиков в корзине?
11) В коробке 20 карандашей: жёлтые и красные. Известно, что среди любых 8 карандашей имеется хотя бы один жёлтый, а среди любых 14 карандашей – хотя бы один красный. Сколько всего жёлтых карандашей в коробке?
12) На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 5 кусков, если по жёлтым — 7 кусков, а если по зелёным — 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
13) Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 20 капель, а в каждый следующий день — на 3 капли больше, чем в предыдущий. После 15 дней приёма пациент делает перерыв в 3 дня и продолжает принимать лекарство по обратной схеме: в 19-й день он принимает столько же капель, сколько и в 15-й день, а затем ежедневно уменьшает дозу на 3 капли, пока дозировка не станет меньше 3 капель в день. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 200 капель?
14) На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 50 км, между A и C — 40 км, между C и D — 25 км, между D и A — 35 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C.
15) Беговая дорожка для проведения тренировок имеет форму окружности. На ней установлены 4 измерительных прибора в точках А.В,С и D. Расстояние между точками равно длине наименьшей дуги окружности, соединяющей эти точки. Найдите расстояние (в метрах) между точками В и С, если расстояние между А и В равно 650м, между А и С – 400м, между С и D – 550м, а между А и D – 350м.
16) В супермаркете объём продаж минеральной воды носит сезонный характер. В январе и феврале было продано по 20 упаковок, а с марта продажи увеличивались на 40 упаковок по сравнению с предыдущим месяцем. С сентября объём продаж начинал уменьшаться на 60 упаковок каждый месяц относительно предыдущего месяца. Сколько упаковок минеральной воды продал магазин за год?
17) На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса?
• Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
18) Прямоугольник разбит на 4 маленьких прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с верхнего левого и далее по часовой стрелке, равны 10,2, 6. Найдите площадь четвертого прямоугольника?
19) Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 9?
20) Ящики двух видов, имеющие одинаковую ширину и высоту, укладывают на складе в один ряд длиной 43м, приставляя друг к другу по ширине. Ящики одного вида имеют длину 2м, а другого-5м. Какое наибольшее число ящиков потребуется для заполнения всего ряда без образования пустых мест?
21) В таблице 3 столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 98, во втором -103, в третьем - 99, а сумма чисел каждой строке больше 26, но меньше 29. Сколько всего строк в таблице?
22) Список викторины состоит из 32 вопросов. За каждый правильный ответ ученик получал 5 очков, за каждый неправильный ответ с него снимали 9 очков, при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 75 очков, если известно, что он по крайней мере 2 раза ошибся?
Домашнее задание на 27 февраля 2017г.
Решить вариант №5 (база или профиль на выбор). Варианты ниже.
Вариант 5 (база)
1. Найдите значение выражения: 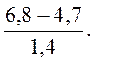
2. Найдите значение выражения: 
3. На первом этаже в каждом подъезде восьмиэтажного дома расположены 2 квартиры, а на остальных – по 4. Какой этаж выбирает в лифте Вася, если он живет в 54 квартире?
4. Среднее гармоническое трёх чисел а, b и с, вычисляется по формуле  Найти среднее гармоническое чисел
Найти среднее гармоническое чисел 
5. Вычислите:  .
.
6. В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 июня счётчик показывал расход 100куб.м воды, а 1июля – 110куб.м. Какую сумму должен заплатить Алексей за холодную воду за июнь, если цена за один куб.м холодной воды составляет 9р.10коп.? Ответ дайте в рублях.
7. Найдите корень уравнения 
8. На клетчатой бумаге с размером клетки  изображён треугольник. Найдите его площадь. Ответ дайте в квадратных сантиметрах.
изображён треугольник. Найдите его площадь. Ответ дайте в квадратных сантиметрах.

9. Установите соответствие между величинами и их возможными значениями.
ВЕЛИЧИНЫ ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) толщина волоса 1) 40 000 км
Б) рост новорождённого 2) 50 см
В) длина футбольного поля 3) 0,1 мм
Г) длина экватора 4) 90 м
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
| А | Б | В | Г |
10. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
11. На диаграмме показано среднемесячное количество осадков, выпавших в Севастополе в 2011 году. По горизонтали указываются месяцы, по вертикали — среднемесячное количество осадков, выпавших в соответствующий месяц, в миллиметрах.
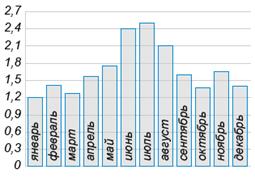
Определите по диаграмме наименьшее среднемесячное количество осадков. Ответ дайте в миллиметрах.
12. Из пункта А в пункт D ведут три дороги. Через пункт В едет грузовик со средней скоростью 44 км/ч, через пункт С едет автобус со средней скоростью 36 км/ч. Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 48 км/ч. На схеме указаны расстояние между пунктами в километрах. Автобус, грузовик и автомобиль одновременно выехали из пункта А.

Какая машина добралась до D позже других? В ответе укажите, сколько часов она находилась в дороге.
13. Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.

14. На диаграмме изображена стоимость акций компании в период с 1 по 14 сентября 2013 года. По горизонтали указывается число месяца, по вертикали – стоимость одной акции в рублях.

Пользуясь диаграммой, поставьте в соответствие каждому из указанных периодов времени характеристику стоимости акций.
ПЕРИОД ВРЕМЕНИ ХАРАКТЕРИСТИКА СТОИМОСТИ АКЦИЙ
А) 1 – 3.09.2012 1) стоимость акций достигла максимума
Б) 3 – 5.09.2012 2) медленный рост
В) 7 – 9.09.2012 3) медленное падение
Г) 10 – 12.09.2012 4) стоимость акций сначала упала, а затем поднялась
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В | Г |
15. На окружности радиуса  взята точка В. Отрезок АС - диаметр окружности, ВС = 6. Найдите АВ.
взята точка В. Отрезок АС - диаметр окружности, ВС = 6. Найдите АВ.

16. Дано два цилиндра. Объём первого цилиндра равен 70. У второго цилиндра высота в 3 раза больше, а радиус основания в 2 раза меньше, чем у первого. Найдите объём второго цилиндра.

17. Поставьте в соответствие каждому неравенству множество его решений.
НЕРАВЕНСТВА РЕШЕНИЯ
А)  1)
1) 

Б) 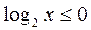 2)
2) 
В)  3)
3) 
Г)  4)
4) 
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
| А | Б | В | Г |
18. Маша старше Влада и Коли, Коля старше Тимы и Стаса, а Оля младше Влада и Тимы.
Выберите утверждения, которые следуют из приведённых данных.
1)Влад младше Стаса.
2)Оля младше Маши
3)Стас старше Оли.
4)Коля старше Оли.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Сумма квадратов цифр двузначного числа равна 13. Если от этого числа отнять 9, то получим число, записанное теми же цифрами, но в обратном порядке. Найдите число.
20. Хозяин договорился с рабочими вырыть ему колодец с таким условием: за первый метр глубины он заплатит им 4200 рублей, а за каждый следующий метр – на 1300 рублей больше, чем за предыдущий. Сколько денег будет должен хозяин рабочим, если они выроют колодец глубиной 11 метров?
Вариант 5 (профиль)



















