Пусть A, B, C – матрицы размерности  .
.
1. Коммутативность суммы матриц
 .
.
2. Ассоциативность суммы
 .
.
3. Дистрибутивность
 ,
,
 ,
,
 - числа.
- числа.
4. Ассоциативность произведения
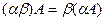 ,
,
 - числа.
- числа.
5. 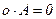 , где
, где  - нулевая матрица.
- нулевая матрица.
6.  , где
, где  - нулевая матрица.
- нулевая матрица.
Определение 3. Произведением матрицы  (размерности
(размерности  ) на матрицу
) на матрицу  (размерности
(размерности  ) называется матрица
) называется матрица  , элементы которой вычисляются по формулам:
, элементы которой вычисляются по формулам:
 , (2)
, (2)

Пример 3.

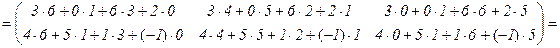
 .
.
Замечание 1. Из определения 3 следует, что умножить матрицу  на матрицу
на матрицу 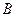 можно лишь в том случае, когда число столбцов в матрице
можно лишь в том случае, когда число столбцов в матрице  равно числу строк в матрице
равно числу строк в матрице 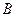 .
.
Замечание 2. Пусть  - квадратная матрица n -ого порядка, а
- квадратная матрица n -ого порядка, а  - единичная матрица также n -ого порядка, тогда
- единичная матрица также n -ого порядка, тогда
 . (3)
. (3)
В самом деле, по определению умножения матриц, имеем
 .
.
Аналогичным образом получаем, что 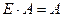 .
.
 Свойства умножения матриц.
Свойства умножения матриц.
1. Ассоциативность
 , где
, где  ,
, 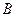 ,
,  - матрицы размерности соответственно:
- матрицы размерности соответственно:  ,
,  ,
,  .
.
2. Дистрибутивность

 ,
,
где  и
и 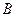 - матрицы размерности
- матрицы размерности  ,
,  - матрица размерности
- матрица размерности  .
.
3.  ,
,
где  - число,
- число,  и
и 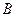 - матрицы размерности соответственно
- матрицы размерности соответственно  и
и  .
.
Замечание 3. Произведение матриц в общем случае некоммутативно, т.е.  , если в частности
, если в частности  , то матрицы
, то матрицы  и
и 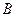 называются перестановочными.
называются перестановочными.
Обратная матрица.
Определение 1. Квадратная матрица  называется невырожденной, если
называется невырожденной, если  и вырожденной, если
и вырожденной, если  .
.
Пусть задана квадратная матрица:
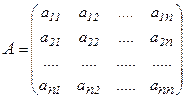 .
.
Определение 2. Матрица 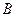 называется обратной к матрице
называется обратной к матрице  , если выполняется равенство
, если выполняется равенство  , где
, где  - единичная матрица. Матрица, обратная к матрице
- единичная матрица. Матрица, обратная к матрице  , обозначается символом
, обозначается символом  :
:
 .
.
Справедлива следующая теорема.
Всякая невырожденная матрица  имеет единственную обратную матрицу.
имеет единственную обратную матрицу.
Пусть задана матрица
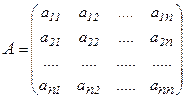
и  , тогда матрицу
, тогда матрицу  можно получить следующим образом:
можно получить следующим образом:
1) вычисляем определитель матрицы 
 ;
;
2) находим матрицу

(заменим в матрице  каждый элемент
каждый элемент  соответствующим ему алгебраическим
соответствующим ему алгебраическим  дополнением
дополнением  );
);
3) транспонируем матрицу 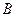 , полученная матрица
, полученная матрица  называется союзной и обозначается символом
называется союзной и обозначается символом  :
:
 ;
;
4) находим матрицу
 .
.
Поясним сказанное на примере:
 .
.
1)  ;
;
2) вычисляем алгебраические дополнения элементов матрицы  и находим матрицы
и находим матрицы 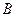 и
и 
 ,
, 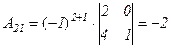 ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,  ;
;
4)  ;
;
5) проверяем:
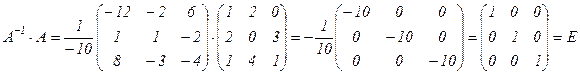 .
.
Легко убедиться, что
 .
.
Ранг матрицы.
Определение 1. Элементарными преобразованиями матрицы называются следующие действия:
1) вычеркивание нулевых строк (столбцов);
2) перестановка двух строк (столбцов);
3) прибавление к одной из строк (столбцу) другой строки (столбца), умноженной на любое число  .
.
Определение 2. Матрица  называется ступенчатой, если ее диагональные элементы
называется ступенчатой, если ее диагональные элементы  , а все элементы, лежащие ниже диагональных, равны нулю (
, а все элементы, лежащие ниже диагональных, равны нулю ( , если
, если  ).
).
Например, матрица
 - ступенчатая.
- ступенчатая.
Теорема 1. Любую матрицу  с помощью элементарных преобразований можно привести к ступенчатому виду.
с помощью элементарных преобразований можно привести к ступенчатому виду.
Теорема 2. При любом способе приведения матрицы  с помощью элементарных преобразований к ступенчатому виду количество строк в полученной ступенчатой матрице будет одним и тем же.
с помощью элементарных преобразований к ступенчатому виду количество строк в полученной ступенчатой матрице будет одним и тем же.
Определение 3. Рангом матрицы  называется число строк в ступенчатой матрице, которая получается из матрицы
называется число строк в ступенчатой матрице, которая получается из матрицы  элементарными преобразованиями. Ранг матрицы обозначается символами:
элементарными преобразованиями. Ранг матрицы обозначается символами: 
Для вычисления ранга матрицы  можно применить следующий алгоритм.
можно применить следующий алгоритм.
1. Вычеркиваем в матрице  все нулевые строки, если они есть.
все нулевые строки, если они есть.
2. Т.к. теперь нулевых строк нет, то в 1-ой строке полученной матрицы найдется хотя бы один отличный от нуля элемент. Переставим столбцы так, чтобы в 1-ой строке на 1-ом месте стоял элемент, отличный от нуля 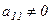 .
.
3. Первую строку, умноженную последовательно на  ;
;  ;
;  ;
;  , прибавим соответственно ко 2-ой, 3-ей, …, m -ой строке. Получим матрицу:
, прибавим соответственно ко 2-ой, 3-ей, …, m -ой строке. Получим матрицу:
 .
.
Вычеркнем в матрице 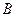 нулевые строки, если они есть. Можно считать, что во 2-ой строке есть хотя бы один элемент, отличный от нуля. Переставим столбцы так, чтобы
нулевые строки, если они есть. Можно считать, что во 2-ой строке есть хотя бы один элемент, отличный от нуля. Переставим столбцы так, чтобы  .
.
4.Умножим 2-ую строку последовательно на  ;
;  ;
;  ;
; 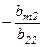 и прибавим соответственно к каждой из последующих строк. В результате получим матрицу
и прибавим соответственно к каждой из последующих строк. В результате получим матрицу
 .
.
Вообще говоря,  , т.к. при переходе от одной матрице к другой некоторые строки (нулевые) могли быть вычеркнуты.
, т.к. при переходе от одной матрице к другой некоторые строки (нулевые) могли быть вычеркнуты.
Повторяя описанные рассуждения через конечное число шагов, мы получим матрицу ступенчатого вида, число строк в которой и будет рангом матрицы  . Поясним сказанное на примере.
. Поясним сказанное на примере.
Вычислим ранг матрицы:
 .
.
Умножим первую строку на «-2» и сложим ее со 2-ой, затем умножим 1-ую строку на «-1» и сложим ее с 3-ей; наконец, первую строку, умноженную на «-5», сложим с 4-ой. Приходим к матрице:
 .
.
В матрице 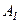 вторую строку, умноженную последовательно на «-2» и «-3», складываем соответственно с 3-ей и 4-ой строками, получаем:
вторую строку, умноженную последовательно на «-2» и «-3», складываем соответственно с 3-ей и 4-ой строками, получаем:
 .
.
Вычеркиваем в матрице 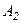 третью и четвертую нулевые строки, получим
третью и четвертую нулевые строки, получим
 ,
,
число строк в ступенчатой матрице  равно 2. Следовательно,
равно 2. Следовательно, 
Теорема 3. Ранг матрицы не меняется при транспонировании.
Рекомендуем читателю транспонировать матрицу  в рассмотренном примере и убедиться, что
в рассмотренном примере и убедиться, что 






