Исследование устойчивости САУ с чистым запаздыванием
 |
Наиболее удобным для исследования рассматриваемых систем является критерий устойчивости Найквиста. Структурная схема САУ будет иметь вид,
представленный на рис.1, где Wo(p) – передаточная функция, включающая в себя объект, силовой преобразователь, датчик и регулятор.
Частотная передаточная функция разомкнутой системы будет иметь вид:
(4)
где: Ао(w) и jo(w) - амплитудно-частотная и фазо-частотная характеристики объекта управления без запаздывания.
. При прохождении АФЧХ через эту точку справедлива следующая система уравнений
где:wk- критическое значение частоты, tk - критическая величина запаздывания.
Или
Величина tk определяется следующим образом. Из первого уравнения системы (5) определяется wk, а из второго tk.
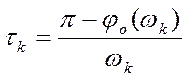(7)
Очевидно, что для нормальной работы замкнутой САУ необходимо, чтобы величина запаздывания была
t < 0,5 tk (8).
Приближенное описание звена с чистым запаздыванием
При исследовании аналитическими методами САУ с запаздыванием применение описания передаточной функцией (3) приводит к трансцендентным уравнениям. Поэтому наряду с точным описанием звена чистого запаздывания применяются приближенные рациональные передаточные функции.
Одно из таких приближений базируется на использовании ряда Тейлора
Следовательно, выражение (3) может быть приблизительно представлено звеном первого порядка
(9)
или звеном второго порядка
(10)
и т.д.
Более точное приближение дает разложение в ряд Паде. При использовании звена первого порядка
(11)
При использовании звена второго порядка
(12)
Компенсация влияния чистого запаздывания в замкнутых САУ
Для нейтрализации вредного влияния запаздывания используются регуляторы, которые компенсируют звено чистого запаздывания. Одним из таких способов компенсации является регулятор Смита. Структурная схема САУ с регулятором Смита представлена на рис.2.
Рис.2.
Wp(p ) - передаточная функция регулятора
Wo(p) - передаточная функция объекта
- передаточная функция модели объекта
- передаточная функция модели запаздывания.
Применяя структурное преобразование схемы на рис.2, получим, что передаточная функция замкнутой системы при 
= Wo(p) и
= t определяется следующим выражением:
(13)
Из (13) видим, что, хотя запаздывание в системе сохраняется (физически это неизбежно), в характеристическом уравнении звено чистого запаздывания отсутствует. Следовательно, действие запаздывания на устойчивость и качество переходных процессов полностью скомпенсировано. Это является несомненным достоинством рассмотренного регулятора.
Недостатком регулятора является его чувствительность к изменениям параметров объекта, которое на практике всегда имеет место.
