преломления и отражения света на сферической поверхности

Преломление света на сферической поверхности и определение фокусных расстояний тонких линз

 

Цель работы: изучение законов преломления лучей на сферической границе раздела двух сред, получение изображений и определение фокусных расстояний тонких линз.

Приборы и принадлежности: оптическая скамья с осветителем и светофильтром, объект-сетка, положительная и отрицательная линзы, экран.

 

Введение

Теория большинства оптических приборов базируется на представлении о световых лучах, распространяющихся прямолинейно в однородном веществе и подчиняющимся законам отражения и преломления света на границе раздела двух сред. Раздел оптики, рассматривающий теорию таких приборов, называемых лучевой или геометрической оптикой.

Каждая светящаяся точка источника света в геометрической оптике рассматривается как вершина расходящегося пучка лучей, называемого гомоцентрическим, т.е. имеющим общий центр. Если после отражения и преломления этот пучок превращается в пучок, сходящийся в одной точке, то и последний является гомоцентрическим пучком, а его центр называется изображением светящейся точки. При сохранении гомоцентричности каждая точка источника дает одну точку изображения. Такие изображения называются точечными или стигматическими.

В силу обратимости световых лучей изображение можно рассматривать как источник, а источник как изображение. При стигматическом изображении центры малых пучков называются сопряженными точками той оптической системы, в которой происходит преобразование расходящегося гомоцентрического пучка в сходящийся.

Соответственные лучи и пучки также называются сопряженными. Поверхность, нормальная к лучам, называется волновой поверхностью. Волновая поверхность гомоцентрического пучка в однородной изотропной среде есть, очевидно, сферическая поверхность.

Если в результате отражения и преломления в оптической системе пучок перестает быть гомоцентрическим, то волновая поверхность перестает быть сферической. Стигматичность изображения точки перестает быть точечным.

Задача практической оптики заключается в получении изображений, точно передающих форму источника (предмета), поэтому важнейшим вопросом лучевой оптики является создание и сохранение условий гомоцентричности пучков.

 

Краткая теория

преломления и отражения света на сферической поверхности

Подробное рассмотрение этого вопроса важно потому, что в качестве преломляющих и отражающих поверхностей в большинстве оптических приборов применяются плоские или сферические поверхности, т.к. изготовление и качественная обработка поверхности другой формы значительно сложнее.

Пусть две однородные среды с показателем преломления 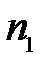и 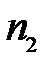разделены сферической поверхностью с радиусом кривизны 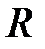и центром кривизны , рис.1.

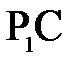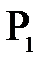Прямая , проходящая через центр кривизны и точечный источник (или произвольно выбранную точку произвольного источника), называется главной оптической осью сферической поверхности.

Изображением т. 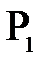, лежащей на главной оптической оси, будет
т. 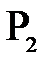, лежащая, согласно закону преломления, так же на главной оптической оси.

 

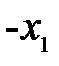
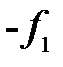
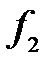
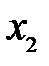
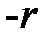
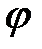
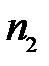
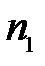
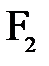
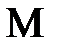
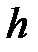
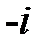
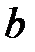
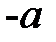
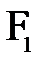
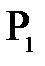
Рис.1.

 

Используя законы преломления и отражения света при построении изображений в оптических системах, здесь и в дальнейшем, условимся пользоваться следующими правилами знаков для углов и расстояний:

а) все расстояния отсчитываются от вершины сферической поверхности (точка пересечения главной оптической оси со сферической поверхностью) и считаются положительными, если они направлены в сторону распространения света от источника и сферической поверхности;

б) углы отсчитываются от направления главной оптической оси (или нормали к сферической поверхности) и считаются положительными, если они отсчитываются по часовой стрелке.

На чертеже будем отмечать только положительные значения длин и углов. Если какая-нибудь величина по принятому условию отрицательна, то для получения положительной величины перед ней будем ставить знак минус.

Рассмотрим узкий гомоцентрический пучок лучей, падающий из т. 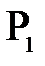на поверхности раздела двух сред. Положим пучок настолько узким, что практически можно считать отрезок 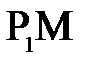равным 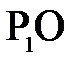, а 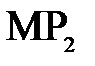равным 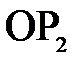и т. д. такие лучи, составляющие с главной оптической осью малые углы, называются параксиальными (приосевыми).

По закону преломления:

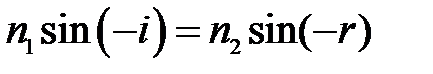(1)

Для параксиальных лучей .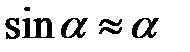

Заменяя в формуле (1) синусы углов через углы, получим:

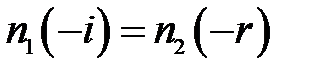(2)

Из треугольника 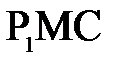и 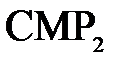(рис. 1) имеем:

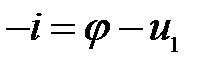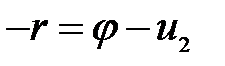, (3)

Подставляя (3) и (2) и учитывая, что 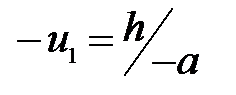, , 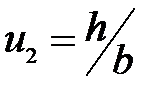, 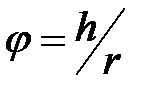получим:

(4)

При преломлении величина 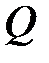, как видно из (4), сохраняет свое значение. Она носит название нулевого варианта Аббе.

Удобнее, представить формулу (4) в следующем виде:

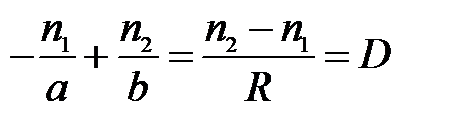(5)

Величина 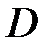называется оптической силой преломляющей поверхности.

Из формулы (5) следует, что при соблюдении параксиальности лучей заданной величине 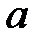вне зависимости от 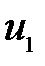соответствует определенное значение 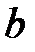. Это значит, что все лучи параксиального пучка исходящего из точки 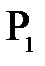соберутся в сопряженной точке 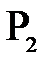, т.е. преломленный пучок так же будет гомоцентрическим.

Если 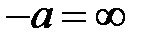(предмет находится на бесконечно большом расстоянии), то:

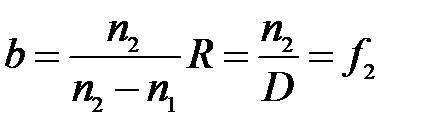(6)

Точка 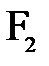, где соберутся параксиальные лучи, идущие из бесконечности (или лучи, идущие параллельно главной оптической оси), называется вторым главным фокусом преломляющей поверхности.

Расстояние 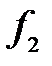называется вторым главным фокусным расстоянием. Первым главным фокусом 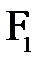назовем точку, удовлетворяющую следующему условию: при помещении в эту точку точечного источника 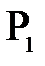после преломления должен возникнуть пучок параллельных лучей (т.е. 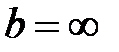). Расстояние 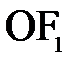равно:

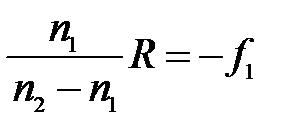(7)

Разделив правые и левые части (6) и(7), друг на друга, получим:

(8)

Разделив правую и левую часть равенства (5) на величину 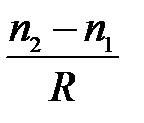получим:

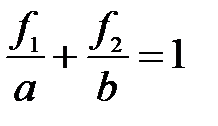(9)

Формуле (9) можно придать несколько иной вид. Для этого введем в рассмотрение отрезки, определяющие положение точек 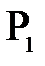и 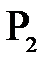относительно фокусов 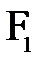и 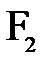. Соблюдая правило знаков (расстояние 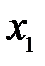и 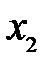отсчитываются от соответствующих фокусов), из рис. 1 имеем:

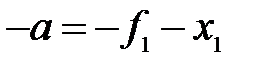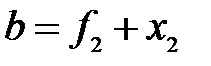, (10)

Подставляя эти значения в формулу (9), получим после преобразований:

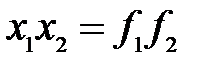(11)

Формула (11) называется формулой Ньютона.

Сравнивая (5), (6) и (7), легко убедиться, что: 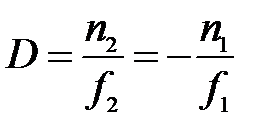(12)

Результаты, полученные для преломляющих сферических поверхностей могут быть применены и для отражающих сферических поверхностей (сферических зеркал), если использовать введенное ранее правило знаков для углов, (рис. 2).

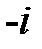
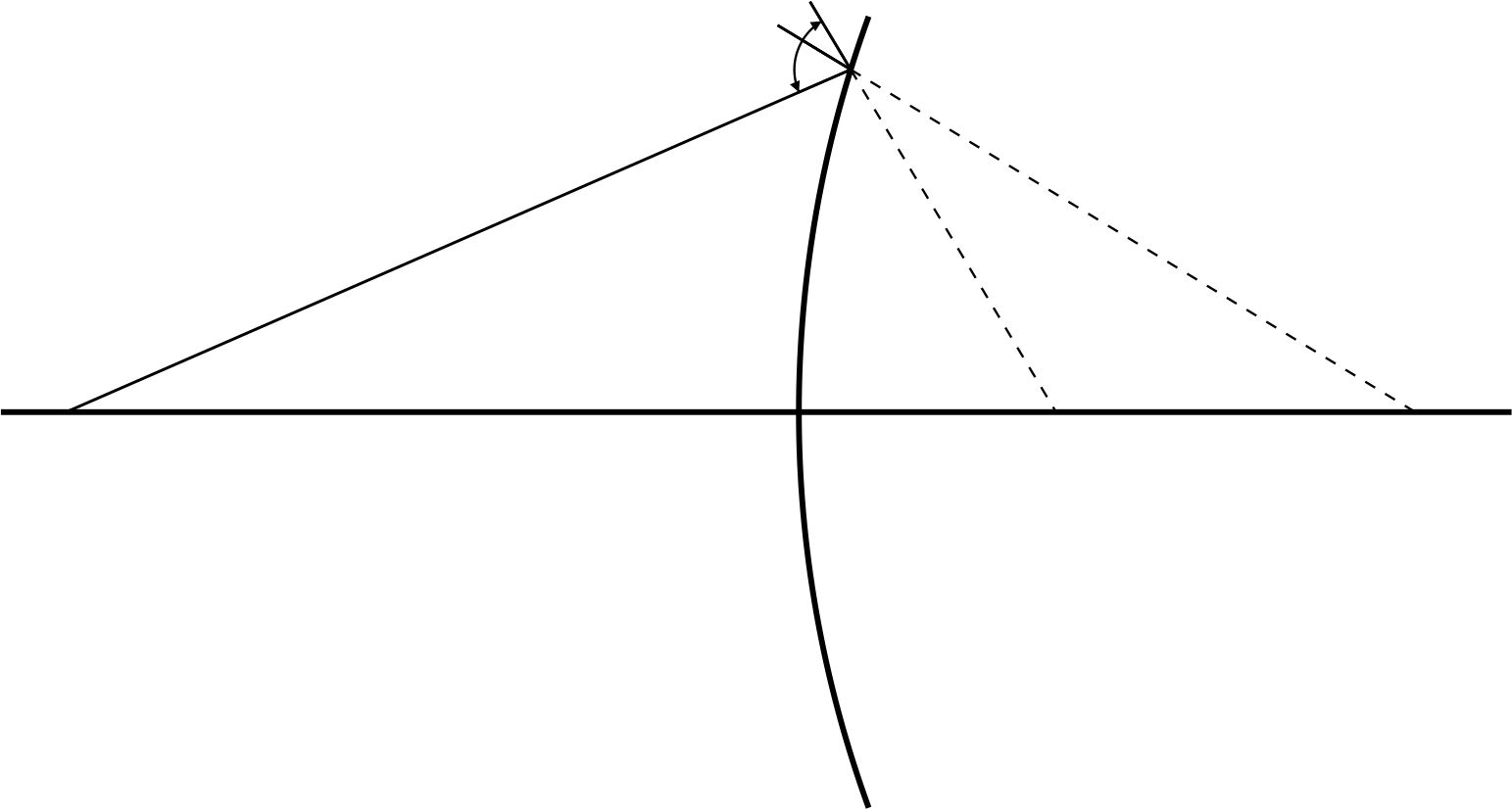
Рис. 2.

 

По закону отражения:

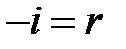(13)

Соотношение (13) формально может быть получено из закона преломления (1), если положить .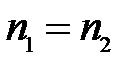

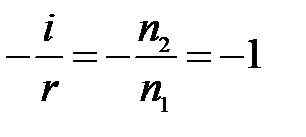(14)

На основании этого можно сделать вывод, что любую формулу, выведенную для преломляющей поверхности, можно использовать для описания явлений в сферических зеркалах, если учесть соотношение (14).

Так, формула (5) для сферического зеркала примет вид:

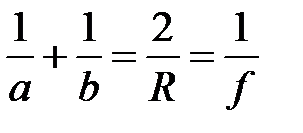(15)

Случай вогнутого и выпуклого зеркала отличается лишь знаком величины 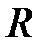. Легко видеть, что фокус вогнутого зеркала – действительный (в нем пересекаются отраженные лучи), а фокус выпуклого зеркала – мнимый (в нем пересекаются продолжения отраженных лучей). В отличие от преломляющей сферической поверхности, сферическое зеркало имеет только один фокус. Правило знаков при определении величин 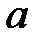, , 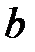, 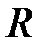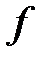– те же, что и в случае преломляющих сферических поверхностей.

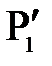
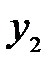
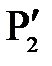
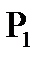– точечный объект, 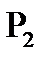– его изображение

рис. 3.

Посмотрим, как при преломлении на сферической поверхности изображается отрезок прямой, перпендикулярной оптической оси.

Посмотрим, как при преломлении на сферической поверхности изображается отрезок прямой, перпендикулярной оптической оси. Повернем ось 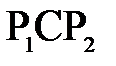вокруг центра кривизны на малый угол 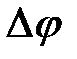. При этом точка 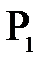опишет дугу 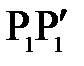, а точка 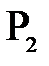– дугу 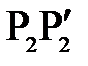. Все точки дуги 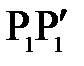отразится соответствующими точками дуги 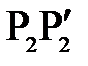. В силу малости этих дуг, заменим их прямолинейными отрезкам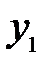и и 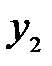, перпендикулярными к оси 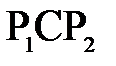(по построению оптическая ось перпендикулярна дугам 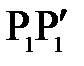и ).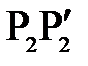

Таким образом, изображением малого отрезка 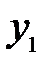перпендикулярного оптической оси, является отрезок 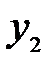, также перпендикулярной к оси. Отсюда вытекает и другой, достаточно очевидный вывод: изображение плоской поверхности 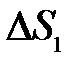, нормальной к оптической оси, есть поверхность 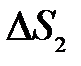, также нормальная к оптической оси.

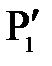
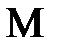
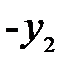
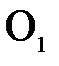
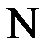
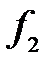
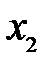
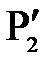
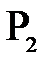
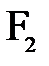
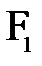
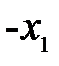
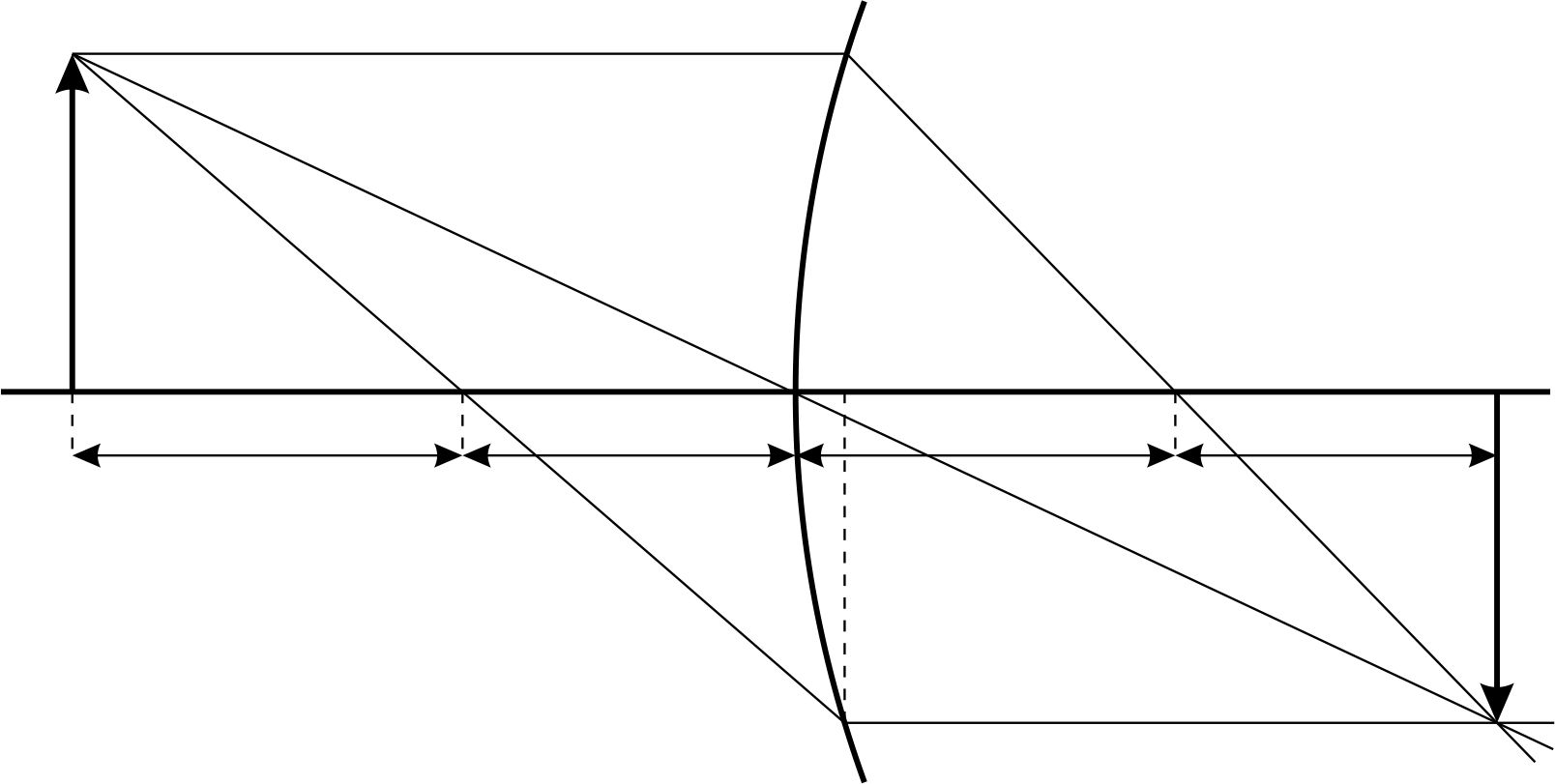
рис. 4

 

Каждая точка изображения является местом пересечения всех лучей, исходящих из соответствующей точки предмета, прошедших через линзу. Для построения изображения точки, достаточно найти пересечение любых двух лучей, ход которых заранее известен. Такими лучами являются:

1. Луч, проходящий через оптический центр линзы – не преломляется и не изменяет своего направления;

2. Луч, параллельный главной оптической оси линзы – после преломления в линзе идет через фокус ;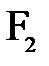

3. Луч, проходящий через фокус 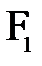– после преломления в линзе идет параллельно главной оптической оси 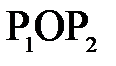линзы.

Для сравнительной характеристики объекта и его изображения введем понятие линейного и углового увеличения.

Назовем линейным увеличением 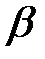отношение линейных размеров изображения к линейным размерам объекта:

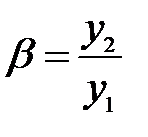(16)

Условимся считать отрезки, перпендикулярные к оптической оси положительными, если они направлены вверх, и отрицательными, если они направлены вниз.

Из треугольника 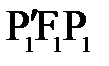и 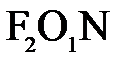находим:

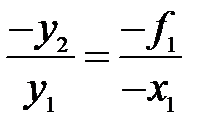(17)

В основании (16) и(17) линейное увеличение:

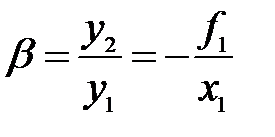(18)

Из теоремы Ньютона (11) имеем:

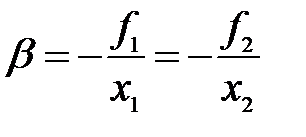(19)

Преобразуем формулу линейного увеличения к другому виду. Для этого дополнительно проведем лучи так, как показано на рис.5

 

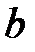
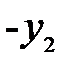
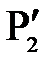
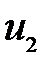
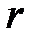
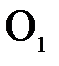
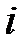
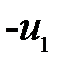
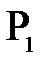
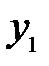
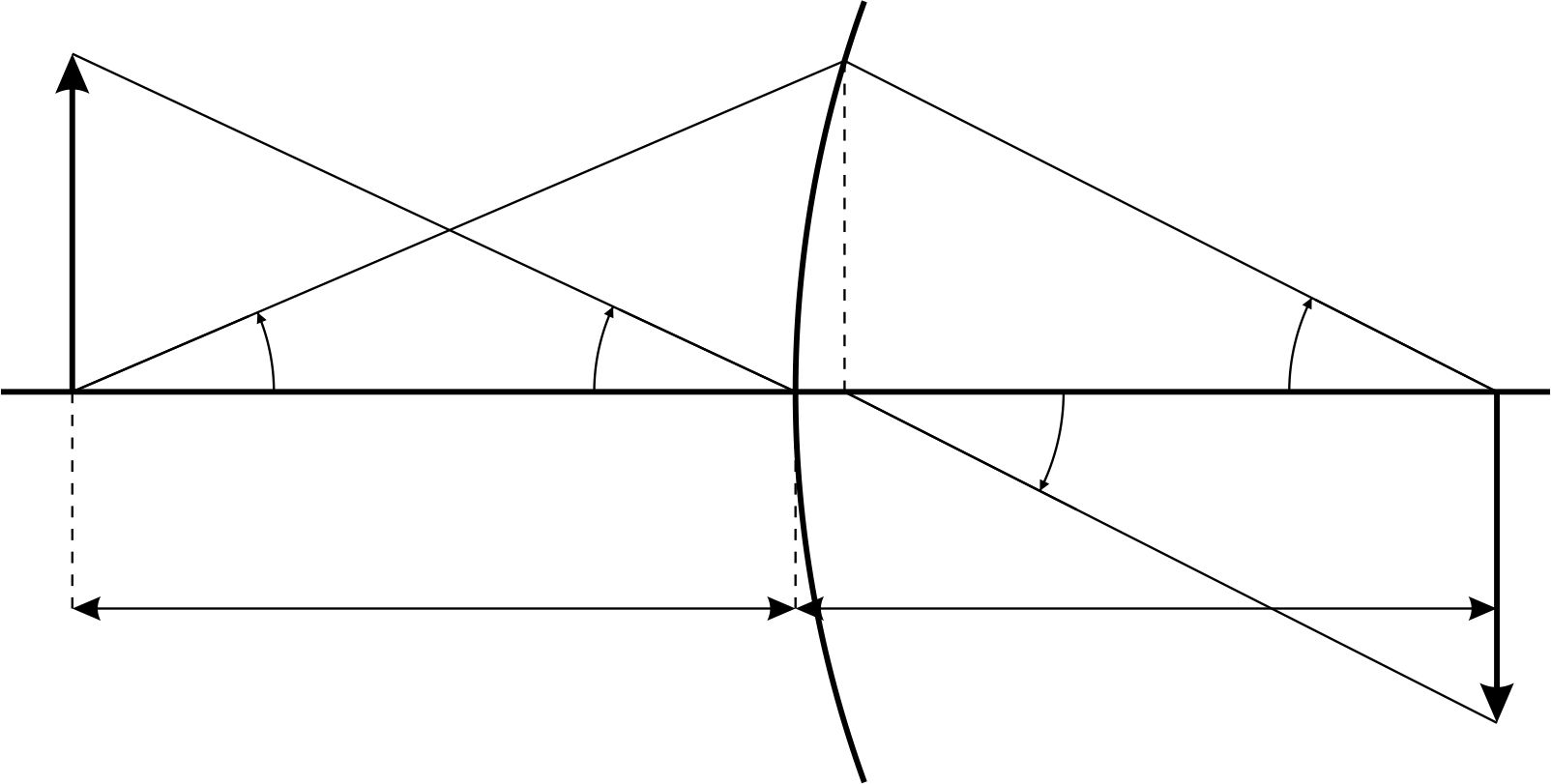
Рис. 5

Для параксиальных лучей (малых углов 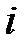, , 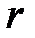, 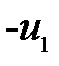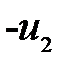) из треугольников 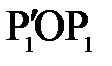и 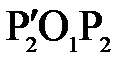вытекают следующие соотношения:

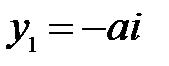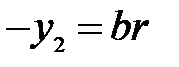
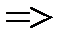
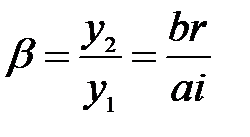, (20)

Закон преломления для малых углов имеет вид:

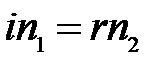(21)

Воспользовавшись последним уравнением системы (20) и соотношением (21), получим:

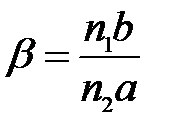(22)

Из треугольников 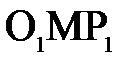и 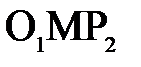для параксиальных лучей следует:

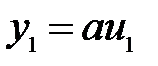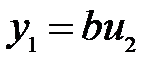
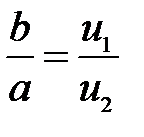, (23)

Подставляя значение 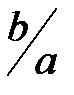из (23) в (22), получим выражение для линейного увеличения:

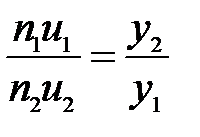, (24)

которое может быть переписано в следующем виде:

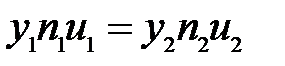(25)

Произведение 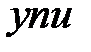носит название инварианта Лагранжа-Гельмгольца.

Угловым увеличением 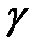называется величина, равная отношению тангенсов углов, под которыми виден предмет с расстояний 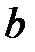и :

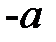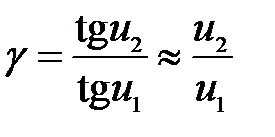(26)

Связь между линейным и угловым увеличением устанавливается на основании формул (24) и (25):

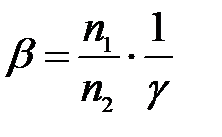(27)

Таким образом, линейное увеличение обратно пропорционально угловому.

Тонкие линзы

Оптическими линзами называются тела, изготовленные из однородного прозрачного в данной области спектра материала и ограниченные поверхности, из которых, по крайней мере одна, имеет радиус кривизны, отличный от нуля. Обычно поверхности, ограничивающие линзу являются сферическими. Материалом для линз, используемых в видимой области, служит стекло, в ультрафиолетовой – главным образом, кварц, в инфракрасной – кристаллы NaCl, KBr, LiF, CaF₂, CsI и др.

Прохождение света через линзу можно рассматривать как последовательное преломление на двух сферических поверхностях (рис. 6)

 

 

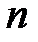
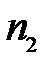
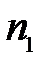
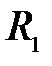
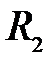
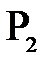
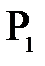
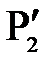
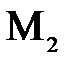
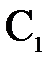
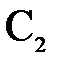
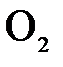
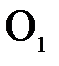
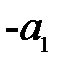
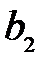
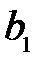
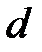
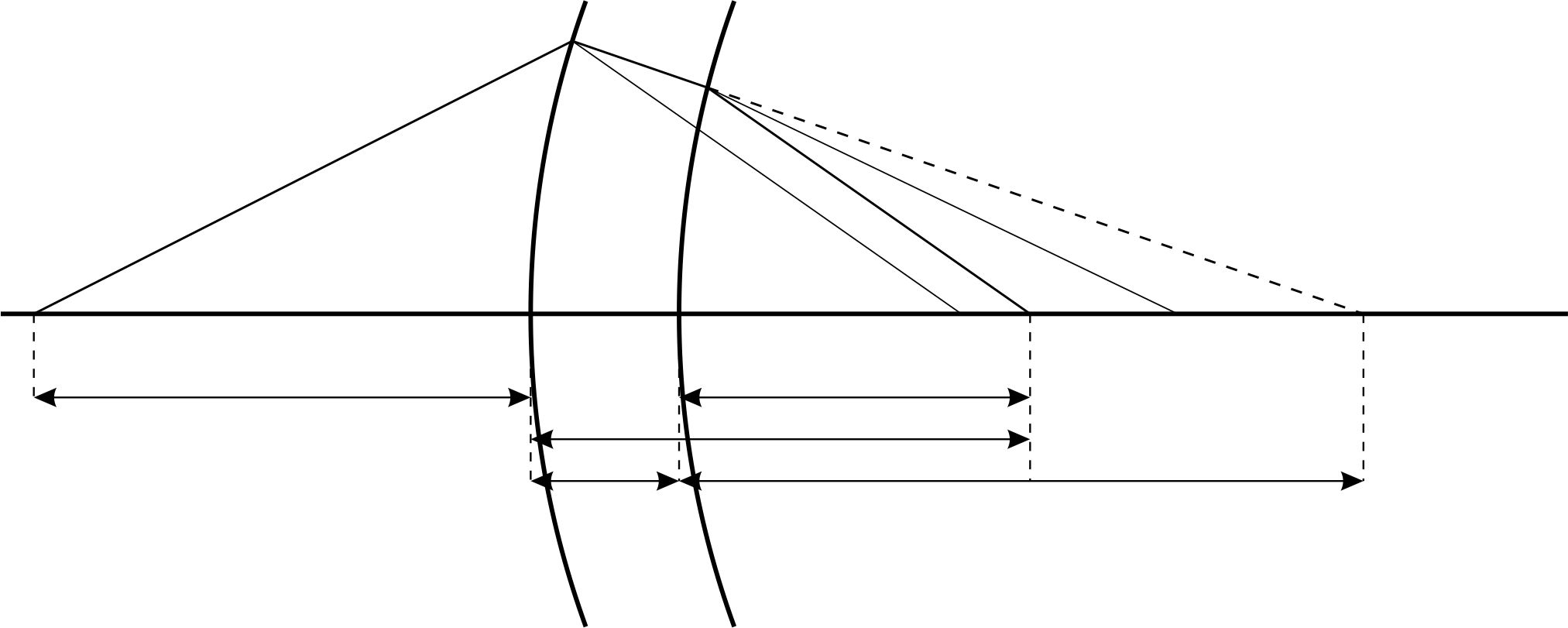
Рис. 6

 

Пусть 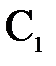и 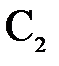– центры сферических поверхностей с радиусами кривизны 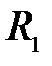и 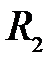. Назовем главной оптической осью системы сферических поверхностей прямую, проходящую через центры кривизны поверхностей. Точк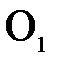и и 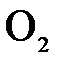пересечения оптической оси со сферическими поверхностями, ограничивающими линзу, называются вершинами сферических поверхностей.

Рассмотрим точечный объект 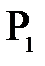, расположенный на главной оптической оси. Если бы имелась лишь одна преломляющая поверхность, то изображение получилось бы в точке 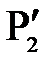. Это изображение нужно рассматривать как объект для второй преломляющей поверхности. Его изображение получится в точке 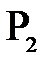. Таким образом, точка 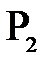будет изображением объекта 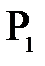, даваемым совокупностью обоих преломляющих поверхностей.

Для нахождения местоположения точки 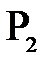применим к каждой из преломляющих поверхностей формулу (5):

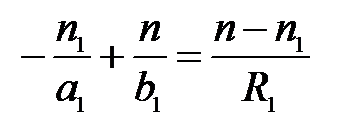(28)

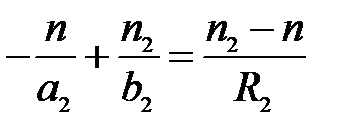(29)

Из рис. 6 видно, что 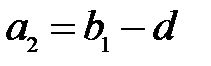. Если рассматривать тонкую линзу, для которой расстояние 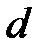между вершинами преломляющих поверхностей мало по сравнению с расстоянием до объекта и изображения, то в пренебрежении толщиной линзы 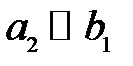и формула (29) перепишется в виде:

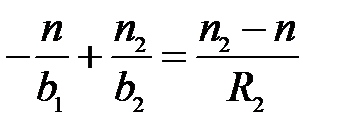(30)

Складывая выражения (28) и (30), получим:

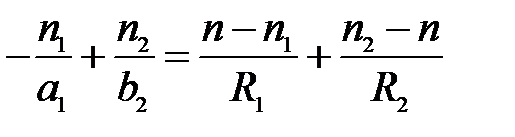(31)

Если линза находится в однородной среде, то приняв обозначения:

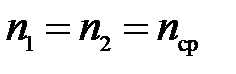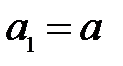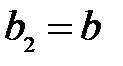, , (32)

Перепишем формулу (31) в виде:

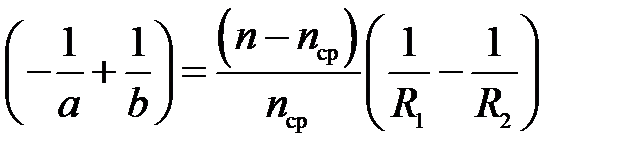(33)

где

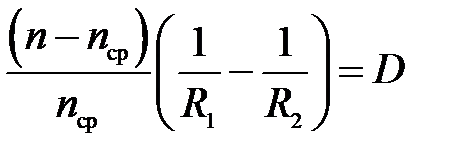(34)

называется оптической силой линзы в данной среде. Легко видеть, что оптическая сила тонкой линзы равна сумме оптических сил ее преломляющих поверхностей:

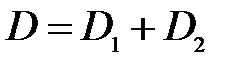(35)

Повторяя рассуждения, приведенные при рассматривании преломления на одной сферической поверхности, найдем фокусные расстояния тонкой линзы:

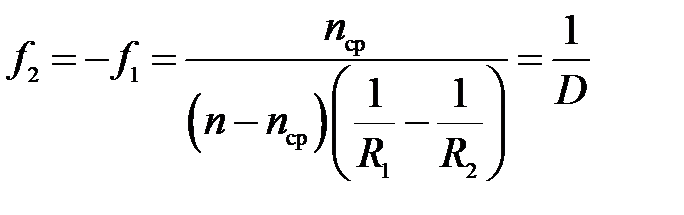(36)

Как правило, величина 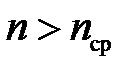, следовательно, знак оптической силы и фокусных расстояний зависит от знака величины .

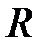На основании формулы (36) формула (33) перепишется в виде:

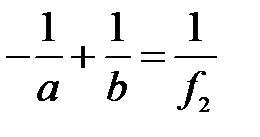(37)

Формулы (33) и (37) обычно называются формулами тонкой линзы.

 

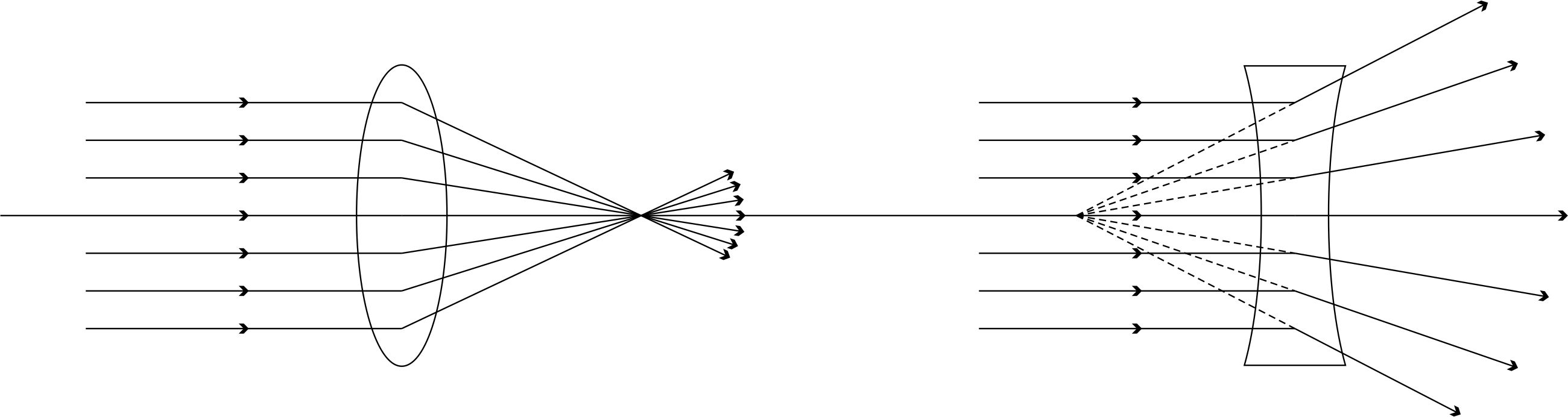
a) б)

Рис. 7

 

Если оптическая сила линзы положительна, то в этом случае линза называется собирательной (положительной) линзой, рис. 7а. Пучок лучей, параллельных главной оптической оси, после преломления в линзе собирается в действительном фокусе линзы. Если отрицательна, то – рассеивающей (отрицательной), рис. 7б. Пучок лучей, параллельных главной оптической оси отрицательной линзы, после прохождения через линзу становится расходящимся, продолжения этих лучей пересекаются в мнимом фокусе.

Пренебрегая толщиной линзы 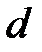(расстояние 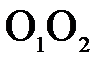между вершинами сферических поверхностей) введем понятие оптического центра тонкой линзы, под которым будем подразумевать точку пересечения плоскости линзы с оптической осью. Участок линзы вблизи оптического центра можно рассматривать как плоскопараллельную пластинку. Как известно, при прохождении луча через плоскопараллельную пластину наблюдается некоторое параллельное смещение по отношению к первоначальному направлению, величина которого зависит от толщины пластины. Если пренебречь толщиной пластины (в данном случае толщиной линзы), то можно считать, что луч, прошедший через оптический центр линзы, не меняет своего первоначального направления. Этим обстоятельством можно воспользоваться при построении изображений предметов в тонких линзах.

 

погрешности оптических систем

Ошибку или погрешность изображения в оптической системе, вызываемую отклонением луча от того направления, по которому он должен был бы идти в идеальной оптической системе, называют Аберрацией оптической системы. Аберрацию характеризуют различного вида нарушения гомоцентричности в структуре пучков лучей, выходящих из оптической системы (пучки, лучи которого не пересекаются в одной точке (не имеют общий фокус).

Аберрацию можно характеризовать как критериями лучевой оптики, так и на основе представлений волновой оптики. В первом случае отступление от гомоцентричности выражается через представление о геометрических аберрациях и фигурах рассеяния лучей в изображениях точек. Во втором случае оценивается деформация прошедшей через оптическую систему сферической световой волны, вводя представление о волновых аберрациях. Оба способа описания взаимосвязаны, описывают одно и то же состояние и различаются лишь формой описания.

Как правило, если объектив обладает большими аберрациями, то их проще характеризовать величинами геометрических аберраций, а если малыми, то на основе представлений волновой оптики.

Наиболее значительны следующие виды аберраций:

Сферическая аберрация – недостаток оптического изображения, заключающийся в том, что световые лучи, прошедшие вблизи оптической оси, и лучи, прошедшие через отдаленные от оси части оптической системы (например, линзы), не собираются в одну точку. Сферическая аберрация может быть практически полностью устранена применением специально рассчитанных комбинаций линз.

Кома – искажение оптического изображения (изображение точки имеет вид капли или кометы), возникающий при косом прохождении световых лучей через оптическую систему. В случае простой линзы размеры пятна пропорциональны квадрату радиуса линзы и углу наклона светового пучка по отношению к оси.

Астигматизм – возникает при больших углах наклона пучка к оптической оси. Если при прохождении оптической системы сферическая световая волна деформируется и перестаёт быть сферической, то пучок лучей становится сложным: лучи пересекаются не в одной точке, а в двух взаимно перпендикулярных отрезках прямой линии, расположенных на некотором расстоянии друг от друга. Такой пучок называется астигматическим, а само явление — астигматизмом.

Дисторсия – аберрация оптической системы, которая выделяется неодинаковостью линейного увеличения в пределах всего поля изображения и приводит к нарушению геометрического подобия между объектом и его изображением.

Оптические системы могут обладать сразу несколькими видами аберраций.

 

Методика и техника эксперимента

Фокусное расстояние тонких линз можно определить различными способами. Как следует из теории тонкой линзы, измерить ее фокусное расстояние можно только с точностью до ее толщины.

Определение фокусного расстояния положительной линзы.

Способ 1. Наиболее простым способом является способ определения фокусного расстояния от линзы до предмета и его изображения. Для этого достаточно измерить расстояния 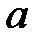и 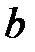, и по формуле тонкой линзы вычислить фокусное расстояние.

При измерениях установить на противоположном от осветителя конце скамьи рейтер с экраном. Вплотную к осветителю поместить светофильтр, а рядом с ним – объект-сетку, играющую роль предмета, между экраном и предметом поместить исследуемую линзу. Перемещая линзу совместно с экраном вдоль скамьи, получить четкое изображение предмета на экране. Затем по линейке, расположенной у основания оптической скамьи, отсчитать расстояния до объект-сетки 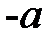и до экрана 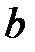. Рекомендуется половину измерений выполнить при увеличенном, половину – при уменьшенном изображении объект-сетки на экране.

Способ 2. (Способ Бесселя) заключается в определении фокусного расстояния по величине перемещения линзы.

В первом способе оказывается существенным, чтобы указатель на рейтере линзы был расположен против ее середины. Во втором способе положение указателя не сказывается на результатах измерений.

Пусть расстояние между предметом и экраном превышает 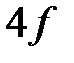. Нетрудно убедиться, что при этом всегда найдется два таких положения линзы, при которых на экране получаются отчетливые увеличенное и уменьшенное изображения предмета, рис.8

При этом оба положения линзы будут симметричны относительно середины расстояния между предметом и изображением. Действительно, воспользовавшись уравнением (37), можно записать для обоих положений линзы:

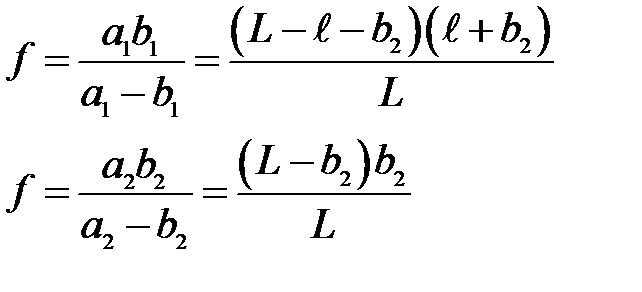(38)

Приравнивая правые части этих уравнений, найдем:

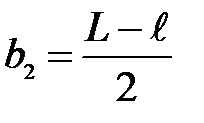(39)

Подставив значение 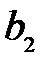в выражение (38):

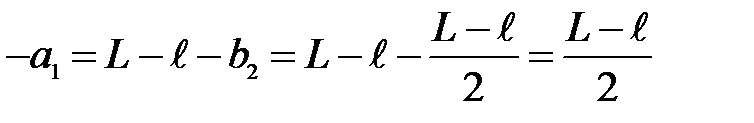(40)

Убеждаемся, что 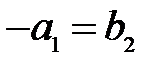, т.е. действительно, оба положения лучей находятся на равных расстояниях от предмета и изображения и, следовательно, симметричны относительно середины расстояния между предметом и изображением.

Воспользовавшись вторым уравнением системы (38) и уравнением (39), получим для фокусного расстояния положительной линзы:

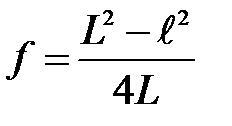(41)

Для определения фокусного расстояния линзы достаточно, таким образом, измерить расстояние 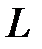между предметом и экраном и расстояние 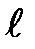между двумя положениями линзы, при которых на экране получаются четкие изображения.

Измерения следует проводить с линзой, используемой в первом способе. Опыт повторить при нескольких расстояниях 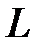и при каждом – повторить несколько раз.

Вычислить радиусы кривизны поверхностей линзы, считая их одинаковыми. Показатель преломления материала линзы для зеленых лучей .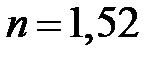

 

Определение фокусного расстояния отрицательной линзы.

Определение фокусного расстояния отрицательной линзы затрудняется тем, изображение предмета получается мнимым, и поэтому не может быть непосредственно получено на экране.

Эту трудность легко обойти с помощью вспомогательной положительной линзы.

Если на пути лучей, выходящих из точки 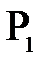и сходящихся в точке 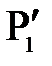после прохождения положительной линзы, рис. 8, поставить рассеивающую линзу так, чтобы расстояние между ними было меньше фокусного расстояния положительной линзы, то изображение точки 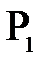сместиться, и окажется в т. .

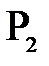Рассмотрим теперь мысленно лучи света, распространяющиеся из т. 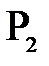в обратную сторону. Тогда в силу оптического принципа взаимности т. 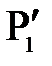будет мнимым изображением т. 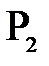после прохождения лучей через рассеивающую линзу.

Воспользовавшись формулой (37) и учитывая правило знаков при таком рассмотрении, легко вычислить фокусное расстояние отрицательной линзы.

 

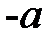
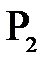
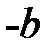
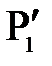
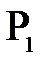
Рис. 8

 

Эксперимент проводят в следующем порядке: поместить на оптическую скамью вспомогательную (положительную) линзу. Перемещая одновременно экран и линзу, добиться отчетливого уменьшенного изображение сетки. После этого, необходимо запомнить положение экрана на скамье.

После чего, между экраном и вспомогательной линзой помещают исследуемую (отрицательную) линзу и вновь находят отчетливое изображение сетки, перемещая отрицательную линзу и экран, при этом необходимо следить, чтобы исследуемая линза не вышла за пределы фокусного расстояния вспомогательной линзы. Все измерения вносятся в таблицу.

Затем, исследуемую линзу убирают, а положение вспомогательной линзы и экрана сбивается. Опыт повторяют не менее десяти раз.

Также, как и в случае положительной линзы, вычислить радиусы кривизны ее поверхностей, считая их одинаковыми ().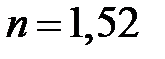

Результаты измерений и вычислений представить в табличном виде:

Собирающая (положительная) линза
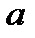№	, см	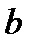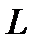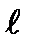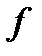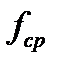, см	, см	, см	, см	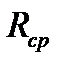, см	, см	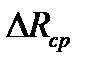, см	, см
1. 2. ⋮ 10.

 

Рассеивающая (отрицательная) линза
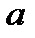№	, см	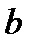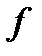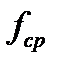, см	, см	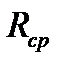, см	, см	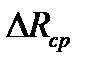, см	, см
1. 2. ⋮ 10.

 

Контрольные вопросы

 

1. Каковы основные характеристики тонкой линзы?

2. Каково правило знаков величин, входящих в формулу линзы?

3. Как строятся изображения предметов в тонких линзах?

4. Как изменится изображение, даваемое линзой, если половину линзы закрыть непрозрачным экраном? Почему?

5. В чем заключается физический смысл оптической силы?

6. Каковы погрешности оптических систем и способы их устранения?

 

Литература

 

1. Г.С. Лансберг. Оптика. М.: Наука, 1976, 926 с

2. Д.В. Сивухин. Общий курс Физики. Оптика. М.: Наука, 1985, 752 с.

3. И.В.Савельев. Волны. Оптика.