Пусть дана СЛАУ порядка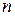 
относительно 
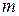неизвестных:
, 
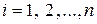(2.7.11)
и при этом количество неизвестных меньше количества уравнений: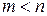 
. В общем случае, такая система является несовместной и не имеет точного решения. Тогда можно найти оптимальное решение, т.е. такое, при котором сумма
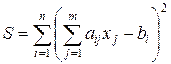(2.7.12)
достигает своего минимума.
Сумма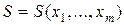 
– функция 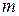переменных. Для определения точки минимума 
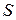(оптимального решения) повторяем аналогичные выкладки из пункта 2.7.1:
.
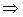
Меняя порядок суммирования, получим СЛАУ относительно оптимальных значений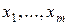 
:
, 
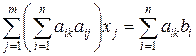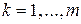(2.7.13)
или в векторно-матричной форме:
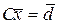, (2.7.14)
где коэффициенты матрицы и компоненты вектора правой части системы вычисляются по формулам
 ,  ;
| (2.7.15) |
 ,
|
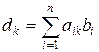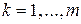
или
; 
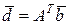. (2.7.16)
Пример 3.7.1. Пусть требуется найти оптимальное решение системы уравнений
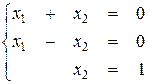
Составим систему уравнений относительно оптимального решения
;
;
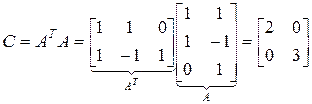Полученная система имеет вид
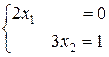
Решением этой СЛАУ (оптимальным решением исходной СЛАУ) будут следующие значения: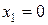 
, 
.
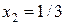Лабораторная работа 2.7.
Построение оптимальной прямой по методу наименьших квадратов
Задание.
Требуется определить оптимальную прямую для заданных точек на плоскости с координатами (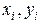
) (требуется составить программу в системе MATLAB (M-языке) и/или на языке Fortran и выполнить ручной счет).
Варианты задания.
Для расчета на ЭВМ следует взять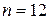 
точек.
Для ручного счета 
точки.
Точки берутся из таблиц Л.2.7.1 – Л.2.7.2 подряд, начиная с номера 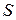студента по журналу.
Таблица Л.2.7.1. Варианты заданий.
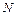
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
| 2 3 3 5 6 7 13 13 11 10 9 8 2 2 4 5 6 7 8 8 3 9 11 |
| 1 2 3 4 7 7 15 17 11.5 10 8 6.5 1 3 4 5.5 6 6.5 7 9 3 8 10 |
Таблица Л.2.7.2. Варианты заданий (продолжение).
|
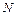
| 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
|
| 13 14 14 8 5 7 12 2 1 8 15 12 12 7 5 9 6 7 7 5 |
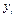
| 12 13 14 9 6 7 11 1 1 7 15 13 12 6.5 5 8 6 6.5 8 4 |
Пример выполнения лабораторной работы.
Пусть заданы координаты точек, представленные в таблице Л.2.7.3.
Таблица Л.2.7.3. Координаты заданных точек.
| ||||||||||||
| ||||||||||||
|
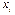
| 2.5 | 4.5 |
Ручной счет.
Расчет сведен в табличную форму (см. таблицу Л.2.7.4).
Подставляем полученные значения в систему уравнений относительно коэффициентов оптимальной прямой 
и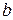 
:
Таблица Л.2.7.4. Ручной счет.
|
|
|
| 
| 
|
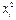
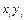
| 2.5 | ||||
| S | 10.5 |
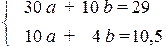
Решая эту систему, например, по методу Крамера, получим:
; 
,
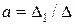где
;
;
.
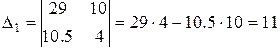Тогда 
; 
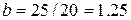
и уравнение оптимальной прямой имеет вид:
.
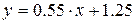Расчет на ЭВМ (Матлаб).
Пример М-файла.
function mnk
x=input('введите массив координат точек по оси x:');
y=input('введите массив координат точек по оси y:');
p1=polyfit(x,y,1);
y1=polyval(p1,x);
fprintf('\nоптимальная прямая: y=(%f)*x+(%f)\n',p1(1),p1(2))
s=sprintf('\noptimal line: y=(%f)*x+(%f)\n',p1(1),p1(2));
plot(x,y,'k*',x,y1,'k-')
grid on,legend('data points','optimal line',0),title(s)
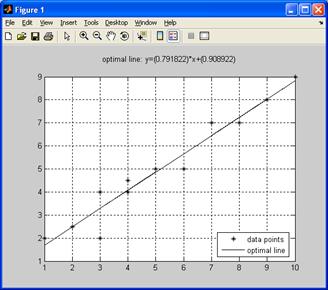
Результаты расчета в командном окне при n=12:
введите массив координат точек по оси x:[1 2 3 4 4 5 3 6 10 8 9 7]
введите массив координат точек по оси y:[2 2.5 2 4 4.5 5 4 5 9 7 8 7]
оптимальная прямая: y=(0.791822)*x+(0.908922)
Замечания.
Для построения аппроксимирующего полинома заданной степени, приближающего функцию одной переменной, заданную соответствующими массивами значений, в системе MATLAB может использоваться функция
polyfit, реализующая метод наименьших квадратов. Имеем: q=polyfit(x,y,n), где y – вектор значений функции; x – вектор значений аргумента; n – порядок аппроксимирующего полинома; p – полученный в результате вектор коэффициентов аппроксимирующего полинома длиной n+1.
