ОСНОВНЫЕ ПОНЯТИЯ
Любую систему автоматического регулирования (САР) можно представить в виде соединения отдельных типовых звеньев. Типовым звеном (ТЗ) называют элемент или узел системы регулирования, который независимо от физической природы процессов, протекающих в нем, одинаково реагирует на один и тот же вид возмущения. Это означает, что два или несколько звеньев САР будут одного типа, если они имеют одинаковую функциональную зависимость между входным и выходным параметрами.
Для всех ТЗ характерны некоторые общие признаки: каждое ТЗ имеет четко обозначенный вход и выход; сигнал через ТЗ распространяется в одном направлении – со входа на выход. В структурных схемах САР типовое звено обозначают в виде прямоугольника, внутри которого записывается его функциональная зависимость, выраженная в операторной форме (передаточная функция).
Разбивка САР на ТЗ облегчает анализ и синтез системы, так как позволяет воспользоваться хорошо разработанными в теории автоматического регулирования (ТАР) методами.
По виду функциональной зависимости ТЗ подразделяются на апериодическое, колебательное, дифференцирующее, интегрирующее, усилительное и звено чистого запаздывания. Это основные типы звеньев, с использованием которых могут быть получены другие типовые звенья, но не более второго порядка (по виду дифференциального уравнения). Уравнения ТЗ систем регулирования выводятся на основе тех или иных физических законов, по которым протекают процессы в звеньях.
ПЕРЕХОДНЫЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ
Переходная характеристика ТЗ представляет собой изменение во времени выходного параметра звена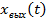 
при ступенчатом входном сигнале и нулевых начальных условиях.
В формуле приняты обозначения:
– величина ступени входного сигнала;
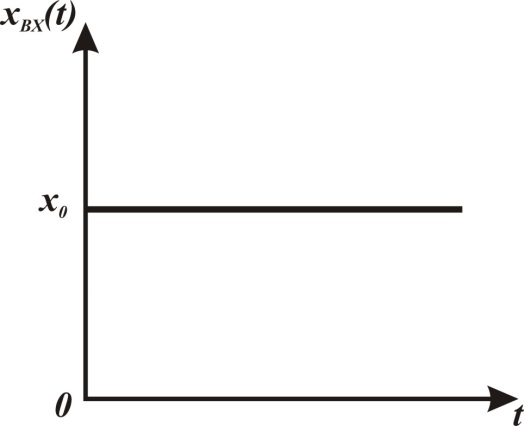
– единичная ступенчатая функция (функция Хевисайда) (рисунок 1).
|
| Рисунок 1 – Ступенчатая функция |
Переходная характеристика или переходная функция определяется как решение дифференциального уравнения ТЗ при ступенчатом входном сигнале.
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ
Частотные характеристики ТЗ получают при гармоническом входном воздействии, заданном либо в тригонометрической форме
либо в экспоненциальной форме
где 
– амплитуда;
– круговая частота;
– начальная фаза входного сигнала;
При этом выходной сигнал изменяется также по гармоническому (рисунок 2) с той же частотой , но с другой амплитудой 
и начальной фазой 
:
Зависимость отношения комплексной амплитуды 
выходного сигнала к комплексной амплитуде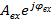 
входного сигнала от частоты колебаний называют частотной функцией, которая будет
где 
– модуль частотной функции или амплитудно-частотная характеристика (АЧХ);
– аргумент частотной функции, или фазо-частотная характеристика (ФЧХ).
Частотная характеристика ТЗ может быть представлена на комплексной плоскости, если предварительно представить частотную функцию в виде
где 
– действительная часть частотной функции;
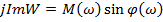– мнимая часть частотной функции.
|
| Рисунок 2 – Осциллограмма колебаний входного и выходного параметров ТЗ при определении его частотных характеристик |
Частотная характеристика ТЗ на комплексной плоскости называется амплитудно-фазо-частотной характеристикой (АФЧХ) типового звена. Частотная функция ТЗ может быть получена из выражении для его передаточной функции 
, представляющей собой отношение изображений то Лапласу выходной величины 
и входной величины 
при нулевых начальных условиях
где 
– оператор Лапласа.
Для получения передаточной функции ТЗ достаточно в дифференциальном уравнении звена произнести замену операции дифференцирования 
наоператор Лапласа входную , и выходную величины, представить их изображениями по Лапласу , 
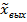и решить это уравнение относительно 
. Если в выражении для заменить на 
, то получим частотную функцию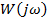 
звена.
ТИПОВЫЕ ЗВЕНЬЯ
