Решение типовых задач контрольной

ЛИНЕЙНАЯ АЛГЕБРА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ, ВАРИАНТЫ ЗАДАНИЙ И ВОПРОСЫ К ЭКЗАМЕНУ

Для студентов экономического факультета

Заочной формы обучения на базе среднего образования

Контрольная работа должна быть выполнена в ученической тетради, на внешней обложке которой следует указать название контрольной работы, фамилию и инициалы студента, полный учебный шифр, место учебы.

Перед решением задач необходимо записывать их условия. Решения задач и пояснения к ним должны быть достаточно подробными. Все вычисления необходимо делать полностью. Для замечаний преподавателя нужно оставлять поля.

Вариант контрольной работы устанавливается согласно последней цифре зачетной книжки (шифра).

Если вариант, к примеру, 8, необходимо решать в контрольной работе задачи с номерами 8, 18 и т.д. Контрольная работа должна быть представлена для проверки не позднее двух недель до начала экзаменационной сессии.

К экзамену студент допускается лишь в случае, если его контрольная работа зачтена.

УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

а) основная литература:

1. Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др.]; под ред. Н.Ш. Кремера. - 3-е изд. - М.: ЮНИТИ-ДАНА, 2013. - 479 с.

2. Математика и информатика. Учебное пособие / В.Б. Уткин, К.В. Балдин, А.В. Рукосуев. - 4-e изд. - М.: Дашков и К, 2011. - 472 с.

 

б) дополнительная литература:

 

3. Кремер Н.Ш. и др. Исследование операций в экономике – М.: Банки и биржи, 2006.

4. Матрицы и системы линейных уравнений: методические указания и задания для самостоятельной работы / Воронежский филиал РРГТЭУ, каф. математики и ЕНД; [сост.: В,Н. Ястребков, И.М. Голев.] – Воронеж, Воронежский ф-л РГТЭУ, 2010. – 55 с.

5. Поленов В.С., Галкин Г.И., Дольский С.В., Черная Ю.В. Сборник заданий по математике для экономических ВУЗов (Аналитическая геометрия). Учебно-методическое пособие для студентов первого курса всех форм обучения всех специальностей. - Воронеж: Воронежский филиал ГОУ ВПО «РГТЭУ», 2006. - 43 с.

6. Щипачев В.С. Курс высшей математики. – М.: Оникс, 2007.

7. Высшая математика. Учебник / К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев; Российская академия образования (РАО). – М.: Флинта: МПСИ, 2010.

8. Математика в примерах и задачах. Учебное пособие / Л.Н. Журбенко, Г.А. Никонова, Н.В. Никонова, О.М. Дягтерева. – М.: Инфра-М, 2010.

9. Высшая математика для экономического бакалавриата: учебник и практикум /Под ред. Н.Ш. Кремера.- 4-е изд., перераб. и доп.- М.: Юрайт, ИД Юрайт, 2012.- 909 с. ISBN 978-5-9919-1526-6(Юрайт). ISBN 978-5-9692-1251-0(ИД Юрайт). ЧЗ

10. Орлова И.В., Полковников В.А. Экономико-математические методы и модели. – М.: ВУЗ, учебник: ИНФРА-М, 2010.

в) программное обеспечение:

1. MS Windows.

2. MS Office.

3. Поисковые системы «Яндекс», «Google» для доступа к тематическим онлайн-калькуляторам.

г) базы данных, информационно-справочные и поисковые системы:

1. Электронно-библиотечная система Znanium: http://znanium.com

2. Научная электронная библиотека ГПНТБ России: http://ellib.gpntb.ru

3. Электронная библиотека «Гумер»: http://www.gumer.info

4. Поисковые системы «Яндекс», «Google» для доступа к тематическим информационным ресурсам.

ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ

В ЗАДАЧАХ 1-10 вычислить определитель: а) разложением по первой строке; б) по правилу треугольника; в) с помощью элементарных преобразований.

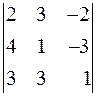
1.	2.	3.	4.	5.
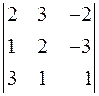
6.	7.	8.	9.	10.

ЗАДАЧАХ 11-20 решить систему уравнений: а) с помощью формул Крамера; б) методом Гаусса

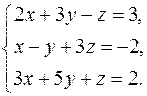
21.	22.	23.
24.	25.	26.
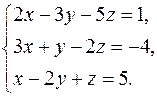
27.	28.	29.
30.

 

 

В ЗАДАЧАХ 21-30 даны координаты вершин треугольника . Найти:

1) длины сторон треугольника;

3) уравнение прямых, описывающих стороны треугольника

Построить заданный треугольник и все линии на координатной плоскости.

А	х1	-14	-11	-15	-13	-10	-12	-14	-16	-17	-18
у1	-7	-13	-16	-15	-12	-9	-10	-11	-11	-11
В	х2	-7	-4	-8	-6	-3	-5	-7	-9	-10	-11
у2
С	х3									-1	-2
у3		-1	-4	-3

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ КОНТРОЛЬНОЙ

РАБОТЫ

РЕШЕНИЕ ЗАДАЧИ ТИПА 1–10

Задача. Вычислить определитель 1) разложением по первой строке; 2) по правилу треугольника; 3) с использованием элементарных преобразований.

Решение. 1) Воспользуемся формулой

.

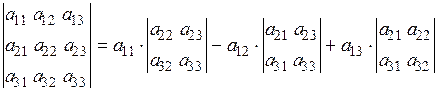В нашем случае

.

2) Правило треугольника имеет вид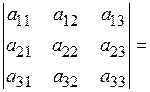

.

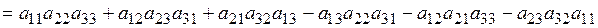Применяя это правило для вычисления заданного определителя, получаем

.

3) Получим с помощью тождественных преобразований из исходного определителя новый, который содержит два нулевых элемента, например, в первом столбце. Для этого сначала умножим первую строку заданного определителя на и результат прибавим ко второй строке определителя. Затем умножим первую строку исходного определителя на 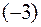и результат прибавим к третьей его строке. В результате получим следующий определитель, равный данному: . Теперь находим значение полученного (а значит, и исходного) определителя с помощью его разложения по элементам первого столбца:

= .

 

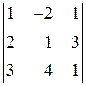РЕШЕНИЕ ЗАДАЧИ ТИПА 11-20

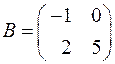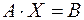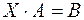Задача. Пусть , , . Требуется решить уравнения 1) , 2) , 3) .

Решение. 1)Вычислим определитель матрицы А:

.

Так как 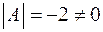, то обратная матрица 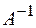существует.

Умножим матричное уравнение на 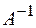слева и проведем преобразования с учетом свойств матричных операций:

,

.

В результате получаем

.

Находим обратную матрицу по формуле , где – присоединенная матрица. Для этого вычисляем алгебраические дополнения элементов матрицы A: , , , . Таким образом, , т.е.

.

Теперь вычисляем искомую матрицу (решение рассматриваемого матричного уравнения):

.

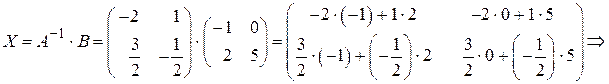
Выполняем проверку:

.

Проверка дала верное равенство, т.е. уравнение решено правильно.

2) Умножим матричное уравнение на 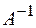справа и проведем преобразования с учетом свойств матричных операций:

,

.

В результате получаем формулу

.

Так как , то

.

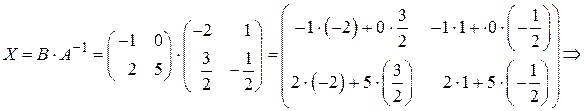
Выполняем проверку:

.

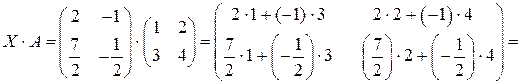
Вывод: уравнение решено верно.

3) Умножаем сначала матричное уравнение на 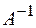слева, а затем полученный результат – на 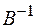справа. В результате искомое решение уравнения выражается формулой

.

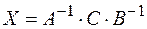Ищем :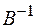

; ;

.

Теперь имеем

.

Остается осуществить проверку правильности полученного результата (сделайте это сами).

РЕШЕНИЕ ЗАДАЧ ТИПА 21–30

Задача1. Т ребуется, используя формулы Крамера, решить систему

Решение. Подсчитаем сначала главный определитель системы , воспользовавшись его разложением по элементам первой строки:

.

У нас

Так как , делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители :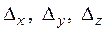

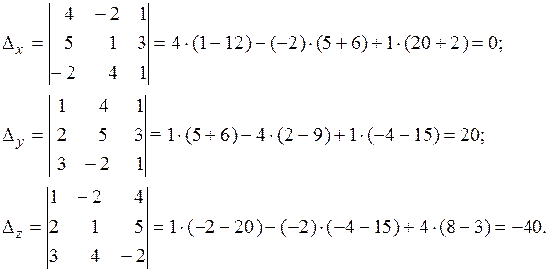
Далее, используя формулами Крамера, окончательно получаем:

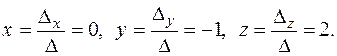
Осуществим проверку правильности решения, подставив его в левую часть каждого уравнения заданной системы:

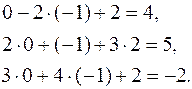
Все три равенства верные, поэтому делаем вывод о правильности полученного решения

Задача 2. Решим систему уравнений из задачи 1 методом Гаусса последовательного исключения неизвестных.

1) Сначала умножим первое уравнение системы на и результат сложим со вторым уравнением системы. Затем первое уравнение системы умножим на (–3) и результат сложим с третьим ее уравнением. В результате указанных тождественных преобразований система примет вид, в котором лишь первое уравнение будет содержать неизвестную величину x:

 

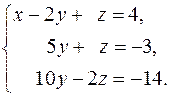
2) Займемся исключением неизвестной y из третьего уравнения последней системы. Для этого умножим второе ее уравнение на 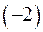и сложим полученный результат с третьим уравнением. В результате получим новую систему, равносильную заданной:

Теперь из третьего уравнения получаем 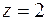, затем из второго – и наконец из первого – . Система решена.

Задача 3. Cистему уравнений 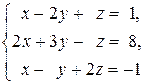записать в матричной форме и решить ее с помощью обратной матрицы.

Решение. Обозначим через матрицу коэффициентов при неизвестных, через – матрицу-столбец неизвестных , а через – матрицу-столбец свободных членов:

, , .

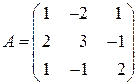С учетом этих обозначений данная система уравнений принимает следующую матричную форму:

. (1)

Если матрица невырожденная, т.е. её определитель отличен от нуля, то она имеет обратную матрицу . Умножив обе части уравнения (1) слева на , получим

,

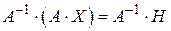т.е.

. (2)

Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения 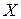системы уравнений (1) необходимо вычислить обратную матрицу .

Пусть имеем невырожденную матрицу

.

Тогда обратная матрица определяется по формуле

,

где (i= 1, 2, 3; j =1, 2, 3) – алгебраическое дополнение элемента в определителе матрицы , которое является произведением на минор (определитель) второго порядка, полученный вычеркиванием i -й строки j -го столбца в определителе матрицы .

Вычислим определитель и алгебраические дополнения его элементов:

, следовательно, матрица имеет обратную матрицу ;

, ,

, ,

, ,

, ,

.

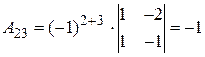Отсюда

.

По формуле (2) находим решение данной системы уравнений в матричной форме:

Отсюда имеем , , .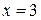

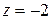Остается сделать проверку, которую предлагаем сделать читателю самостоятельно.

 

 

РЕШЕНИЕ ЗАДАЧИ ТИПА 31–40

 

Задача. Даны координаты вершин треугольника : Требуется найти:

1) длину стороны ;

2) уравнения сторон и 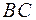, их угловые коэффициенты; 3) внутренний угол при вершине в радианах с точностью до 0,01;

4) уравнение медианы ;

5) уравнение и длину высоты ;

6) уравнение прямой, проходящей через точку параллельно прямой и точку 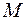ее пересечения с высотой ;

7) уравнение окружности с центром в точке , проходящей через вершину .