Коэффициент корреляции r обладает высокой степенью точности количественной характеристики связи между факторами.
Расчет коэффициента r производится по формуле:
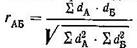
где А и Б - коррелируемые ряды вариант dА и dБ отклонения вариант от средних значений этих рядов (разность между каждым значением варианты ряда и средней арифметической величиной данного ряда). Точность вычисления по формуле должна быть достаточно высокой, не менее двух знаков после запятой.
Последовательность вычисления коэффициента r показана на примере результатов исследования, влияния уровня физической работоспособности лыжников (причинный фактор), выявленного при помощи дозированной нагрузки на велоэргометре, на результат в гонке на 15 км (следственный фактор);
1. Составить таблицу (см. табл. 4) для первичных числовых операций, для чего в первых двух колонках расположить показатели уровня физической работоспособности и показатели спортивного результата в гонке на 15 км; ранжирование показателей не обязательно.
Таблица 4
| Уровень физической работоспособности | Результат гонки | dА | dБ | dА2 | dБ2 | dАdБ |
| А | Б | |||||
| 24,8 | +4,8 | -10 | 23,04 | -48,0 | ||
| 20,1 | +0,1 | -3 | 0,01 | -0,3 | ||
| 20,4 | +0,4 | -2 | 0,16 | -0,8 | ||
| 24,0 | +4,0 | -1 | 16,00 | -4,0 | ||
| 17,5 | -2,5 | +4 | 6,25 | -10,0 | ||
| 16,8 | -3,2 | +6 | 10,24 | -19,2 | ||
| 19,0 | -1,0 | +9 | 1,00 | -9,0 | ||
| 17,2 | -2,8 | +2 | 7,84 | -5,6 | ||
| 24,2 | +4,2 | -12 | 17,64 | -50,4 | ||
| 16,3 | -3,7 | +8 | 13,69 | -29,6 | ||
| SА = 200,3 | SБ = 731 | SdА2 = 95,87» 96 | SdБ2 = 459 | SdАdБ = 176,9» - 177 |
2. Вычислить средние арифметические величины для уровня физической работоспособности и результата гонки:
3. Найти отклонения показателей рядов «А» и «Б» от своих средних арифметических величин (dА и dБ). Например: для уровня работоспособности в 24,8 отклонения от среднего значения будут равны: 24,8-20,0 = +4,8; для спортивного результата в 63 мин.: 63-73 = -10 и т.д.
4. Вычислить квадраты найденных отклонений (dА2 и dБ2). Получим: +4,82 = 23,04; -102=100.
5. Найти суммы квадратов отклонений: SdА2 = 95,87» 96; SdБ2 = 459.
6. Определить произведения отклонений (dАdБ) Получим: (+ 4,8) х (-10) = - 48.
7. Найти сумму произведений отклонений: SdАdБ = 174,9» 177
8. Подставить найденное значение в формулу:
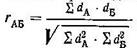
Получим следующее:
= - 0,843
9. Определить достоверность высчитанного коэффициента корреляции.
Установлено, что если парных факторов меньше 100, то оценку достоверности целесообразно производить по таблице (см. табл. 5) критических значений коэффициента корреляции rАБ.
Таблица 5
Критические значения коэффициента корреляции r
| Число корре-лируемых пар, n | Уровень значимости, Р | Число корре-лируемых пар, n | Уровень значимости, Р | ||
| 0,05 | 0,01 | 0,05 | 0,01 | ||
| 0,977 | 0,99988 | ||||
Табличные значения даны для двух уровней значимости: Р = 0,05 и Р = 0,01. Полученный коэффициент корреляции может считаться достоверным лишь в том случае, если его числовое значение превышает табличное значение хотя бы при уровне значимости Р = 0,05 для данного числа парных факторов. В приведенном примере для 10 парных факторов табличные значения составляют: Р0.05 = 0,623, P0.01 = 0,765. Высчитанный коэффициент равен 0,837, т.е. он больше табличного значения при Р = 0,01, что говорит о достоверно существующей связи между исследуемыми показателями. Итоговая запись выглядит следующим образом: r = -0.843, при р ≤ 0,01.
Задания для самостоятельной работы
1. Определите достоверность различий по t-критерию Стьюдента между двумя группами
| Группы | n | ||||||||||
| К | |||||||||||
| Э |
2. Рассчитайте коэффициент корреляции (r)
| Испытуемые | ||||||||||
| Признак А | ||||||||||
| Признак Б |
