Задание 1.1. Программирование формул
Целью работы является освоение программирования алгоритмов с линейной структурой, когда решение задачи является результатом выполнения цепи вычислений, в которой очередные вычислительные действия используют в качестве исходных данных результаты вычислений на предыдущих этапах.
Задание является заголовком столбцов таблицы вариантов заданий и формулами в соответствии с вариантом задания.
Действия по вычислениям промежуточных и окончательных результатов описываются операторами присваивания. Необходимо следить, чтобы порядок расположения операторов присваивания в программе от ее начала к концу соответствовал логической последовательности действий при решении поставленной задачи.
Не следует выражать одни переменные через другие для получения одной формулы из нескольких: в алгоритме и программе необходимо записать столько формул, сколько приводится в задании.
При выборе имен переменных и составлении арифметических выражений необходимо правильно устанавливать тип используемых величин (целые, вещественные и так далее). При использовании в формулах греческого алфавита можно использовать их латинские названия или буквы, сходные по начертанию. Например, символ a можно заменить на Alfa или A, w на Omega или W.
К сожалению, в языке Паскаль имеется ограниченное количество математических функций, поэтому, при отсутствии стандартной функции ее выражают через другие, используя функциональные соотношения. Ниже приводятся основные математические функции, отсутствующие в языке Паскаль:
 ;
;
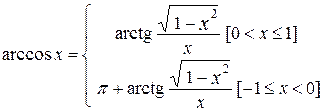 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Более того, любую функцию можно вычислить с помощью четырех арифметических операций итерационными методами или разложением в ряды.
Варианты задания, определенные в соответствии с табл. 1, приведены в табл. 2.
Таблица 2. Варианты заданий 1.1
| № вар. | Вычислить выражение | При заданных значениях |

| 
| |

| 
| |

|   
| |

| 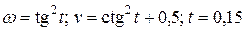
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |
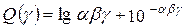
| 
| |

| 
| |

| 
|
Продолжение табл. 2
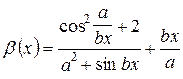
| 
| |

| 
| |

| 
| |

| 
| |
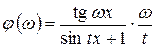
| 
| |

| 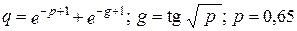
| |

| 
| |

| 
| |

| 
| |

|  
| |

|  
|
Окончание табл. 2

|  
| |

|   
| |

| 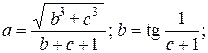 
| |

| 
| |

|  
| |

| 
| |
 
|   
|
Задание 1.2. Ветвящиеся алгоритмы
Логические выражения используются не только для решения задач булевой алгебры, но и для ветвления программы в логических и циклических операторах. Причем последний вариант использования логических выражений применяется наиболее часто.
Логические выражения состоят из логических констант, переменных и отношений, соединенных логическими операциями. В простейших случаях в операторах используют отношения: два выражения, соединенных знаком отношения или сравнения (<, >, >=, <=, =, <>), например I > 20. Но иногда возникают условия, требующие использования более сложных логических выражений.
Пример задания. На плоскости задана фигура (например, рис. 9, усеченный круг, в заданиях область фигуры заштрихована). Вводится точка с координатами X,Y. Определить, принадлежит введенная точка фигуре или нет. В результате анализа должно выводиться: «Введенная точка принадлежит фигуре» или «Введенная точка фигуре не принадлежит». Считать, что точка на границе фигуре принадлежит.

Рис. 9. Пример фигуры
Для определения вхождения точки в круг можно использовать формулу окружности
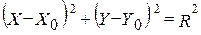 .
.
Соответственно изменив знак = на ≤ получим условие вхождения точки в круг c координатами центра (3,3) и радиусом 3:
 .
.
Кроме этого область, занятая треугольником, так же не входит в закрашенную область, то есть полуплоскость над прямой Y = ‑ X + 7 фигуре не принадлежит. Условия нахождения точки внутри круга и под прямой должны выполняться одновременно. Для этого необходимо использовать логическую операцию AND.
Таким образом логическое выражение
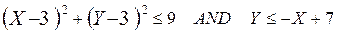
примет истинное значение, если точка входит в закрашенную область, иначе ложное. Тогда в логическом операторе по прямой ветви Then выводится «Введенная точка принадлежит фигуре», а по ветви Else – «Введенная точка фигуре не принадлежит».
Но можно и поменять ветви местами, тогда при вхождении точки в фигуру логическое выражение должно принимать ложное значение. Тривиальный вариант: поставить перед предыдущим выражением знак отрицания NOT. Но более наглядным решением будет составление выражения с условием невхождения точки в фигуру. Здесь должно выполняться хотя бы одно из условий: точка не входит в круг или точка лежит над прямой, соответственно, логическое выражение примет вид:

При выполнении контрольной работы составить два варианта программы (без использования операции NOT) для фигуры, соответствующей варианту задания.
Требование данной работы: описать всю фигуру одним логическим выражением.
Алгоритм этой задачи представляет типичную ветвящуюся структуру с одним блоком ввода, одним блоком решения (анализа вхождения точки) и двумя блоками вывода. Так как размеры блоков должны быть одинаковыми (ромб блока решения не должен превышать блоков ввода-вывода), то при необходимости можно использовать фигуру комментария, представленную на рис. 10.

Рис. 10. Комментарий в блок-схемах алгоритмов
Варианты заданий
1.  2.
2. 
3. 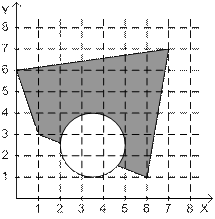 4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
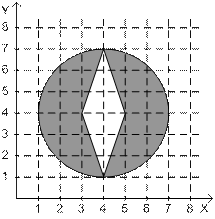
10. 
11.  12.
12. 
13.  14.
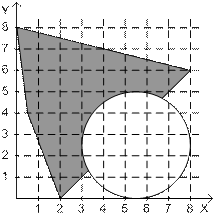
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
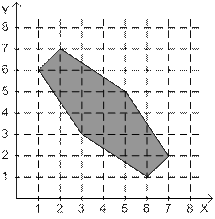
22. 
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 






