Появилась особенность в виде добавления 2-х слагаемых, обусловленных н.у. 
если н.у. нулевые з.Ома приобретает традиционную форму: 
В О.М. появлются особенности при преобразовании //-го соединения
1. t =0
2. переходим к ОИ 
; i 
; 
; 
; 
3. t ≥0 по ВЗК:
Из 1 и 2-го выражаем I1(p) и I2(p) и подставляем в 3 уравнение:
В ОМ при ненулевых н.у. при сворачивании //-го соединения нельзя складывать проводимости, т.к. в изображениях ветвей есть добавки, обусловленные н.у. Если н.у. нулевые, эти добавки →0 и мы получаем:
Получили опр. токи теперь необходимо от них перейти к реальным тока в ветвях.
Формула Римана-Меллина. Допустим, на первом этапе нашли о.и. функции F(p)→I(p) 
i(t); 
чтобы выполнить переход нужно, чтобы интеграл брался, для этого сначала нужно найти особые точки F(p) – о.и., точки ветвления. В этих точках задача теряет однозначное решение. Опр-в эти тчки, выбирают обл-ть интегрир-я так, чтобы они в эту область не попали, а именно на компл. плоскости выбирают прямую интг-я т.о., чтобы особые точки легли левее этой прямой (это делается выбором значения 
)
На практике(**) не применяется, используется в основном теорема разложения:
Пусть получено операторное изображение 
как пр., оно получается в виде рац.дроби, т.к. оп.токи получаются в рез-те деления оп.напряж-я на сопрот-е, в (1) А(p) и В(р) – полиномы. Как пр. разных степеней
Допустим, что (1) правильная дробь, т.е. макс-я степеньзнам-ля больше чем макс-я ст. числ-ля. Возможны два случая:
1. Корни уравнения простые числа
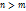1) B(p)=0, p1;p2;pn – эти корни должны совпасть с корнями х.у., однако, может добавиться нулевой корень. Согл. Т.разложения сложную рац. дробь 1 представлют в виде суммы простых дробей
Затем по отдельности каждую дробь переводят в оригиналы, окончательный результат f(t) получают суммированием этих оригиналов. В (***) неизвестные С1, С2 и т.д. Найдем формулы для них. Сначала для С1: (***) умножим на (p-p1)
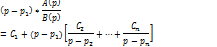Положим, что p=p1: 
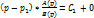В левой части при p=p1 получается неопределенность 0/0, поэтому раскр-м неопрд-ть по правилу Лопиталя:
Переводим все простые дрои в ориг-лы, предвар-но запишем разл-е в общ. Виде
В (2) осущ-м переход к ориг-лу, учитывая, что оригинал есть exp:
т.к. в п.п. должны быть е. Тогда ор-л всей рац.дроби f(t):
В случае нулевого корня
В(р) = 0 среди корней знам. Рац.дроби появл-ся 0 корень, тогда
В этом сл. можно польз-ся формулой (3), но проще переход к ор-лу осуществить по формуле:
(4) записано для нулевого 1-го корня р1=0
Нулевой корень означает, что в ориг-ле (U или I) появится пост.сост-я (график пойдет не от 0)
Несколько приемов перехода к ориг-м:
1. если среди корней зн. В(р)=0 появились кратные корни, то необх использовать теор. свертывания. Пусть получено ОИ – сложное по форме, сначала его представлют в виде произведения более простых членов: F1(p), F2(p)
затем находят ор-лы этих множ-й: 
C пом ф(3) или ф(4), а ориг-л F(p) сложной дроби находят по формуле:
интеграл свертки
1. t=0 м.к.
2.выбираем метод сворачивания
Находим опер-й ток
В уравнении B(р) =0 появилось 2 кратных корня (нулевых) из-за 
Используем т. Свертывания
; 
- нереальный ток, а какой-то множитель, поэтому он = U. В знаменателе (*) появился 0-й корень р0 = 0 и второй корень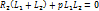 
;
При переходе к оригиналу используем:
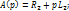
Упрощаем: 
По т.разложения ищем ор-л резул-го тока:
2.Если получившееся изобр-е (I(p) или U(p)) непр-я дробь(степ числителя>ст.знам) можно выделить целую часть, то тогда делим числ-ль на зн-ль(выд-м цел.часть)
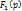- правильная др.
Затем находим ор-л f1(t) по ф(3) или ф(4). Ориг-л первонач-го изоборажения
; 
этот сл. Наблюдается при определенном U на L.
3. По ПЗК и ВЗК в оп.форме необходимо складывать либо оп.токи, либо оп.напряж-я
Тогда ор-л рез-та этого слож-я = сумме оригиналов токов и напряжений.
По ф(3) или (4)
