АНАЛИТИЧЕСКИЙ АНАЛИЗ
ЛИНЕЙНЫХ МНОГОМЕРНЫХ ДИСКРЕТНЫХ СИСТЕМ
Курсовая работа
По дисциплине
«Цифровые системы автоматического управления»
| Выполнил студент ИнЭТМ группы б-УПТСзс41 ЖемчуговА.С. Шпырев А.В. Проверила Торгашова О.Ю. |
Саратов
Оглавление
Введение. 3
Дискретная модель линейной стационарной системы.. 4
Анализ дискретных стационарных систем. 7
Список используемой литературы.. 9
Введение
В современных управляемых системах широко используют элементы и системы, входные и выходные сигналы которых имеют дискретный характер. Среди таких элементов, прежде всего, следует упомянуть управляющие ЦВМ и микроконтроллеры, обмен информацией между которыми и остальными частями системы может происходить лишь в дискретные, то есть отличающиеся на конечную величину, моменты времени. Системы, содержащие такие элементы, называют дискретными или непрерывно-дискретными системами.
Дискретные системы, как и непрерывные системы, имеют несколько форм математического описания во временной области в виде:
- разностных уравнений вход-выход, являющихся аналогом описания непрерывных дифференциальных уравнений;
- взвешенной временной последовательности, являющейся аналогом описания непрерывных систем при помощи импульсной переходной функции;
- разностных уравнений в переменных состояния, являющихся аналогом дифференциальных уравнений в переменных состояния для непрерывных систем.
Дискретная модель линейной стационарной системы
Дискретной моделью уравнений
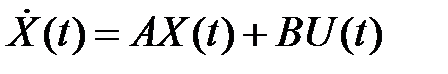, (1)
(2)
называется система разностных уравнений
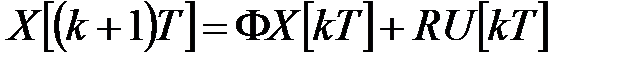, (3)
, (4)
реакция которых x[kT] совпадает в точках t=kT с решениями системы (1),(2), для k=0,1,2,3,…
– 
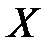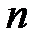-мерный вектор состояний, 
– 
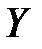-мерный вектор выходных переменных,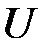 
– 
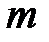-мерный вектор входных переменных (управлений); 
, 
, 
, 
, 
, 
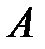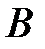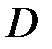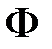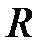– матрицы чисел соответствующих размеров. Матрицы 
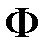и 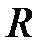связаны с матрицам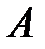и 
и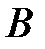 
следующими соотношениями
, (5)
(6)
В случае, если 
– неособенная матрица (
), то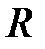 
можно определить следующим образом
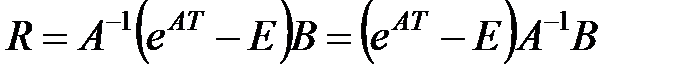(7)
Задана непрерывная модель линейной стационарной системы.
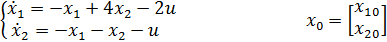
1. Построить дискретную математическую модель систем.
Период дискретности T=1 сек
2. Представим элементы системы в матричном виде
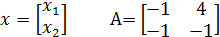
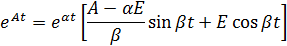
Для определения матриц Φ и R необходимо найти собственные значения λ
= 
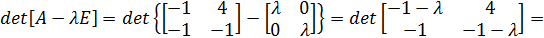
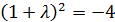
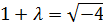
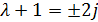
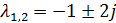
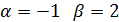
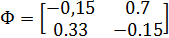
Произведём предварительные расчёты и преобразования для определения матрицы R
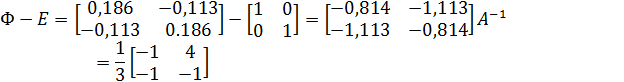
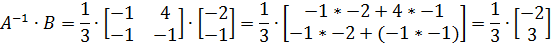
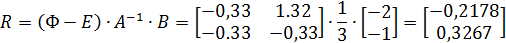
Дискретная математическая модель рассматриваемой системы принимает вид:
=1,8678
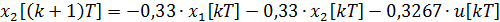= -0,3267
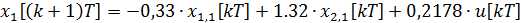=-0,8299
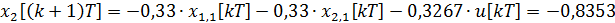
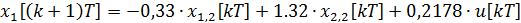=-0,6109
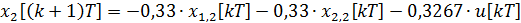=0,2228
=0,7135
=-0,1986
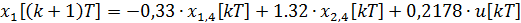=-0,2798
=-0,4966
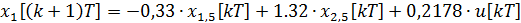=-0,3454
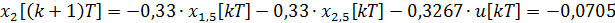
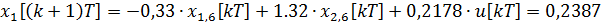
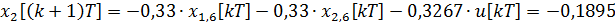
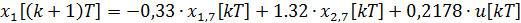=-0,1111
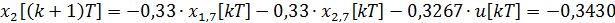
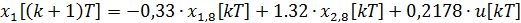=-0,1982
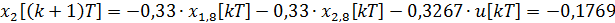
=0,0498
=-0,2029
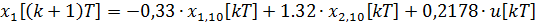=-0,0665
=-0,2762
Анализ дискретных стационарных систем
Для дискретных систем роль дифференциальных уравнений в переменных состояния играют разностные уравнения
, 
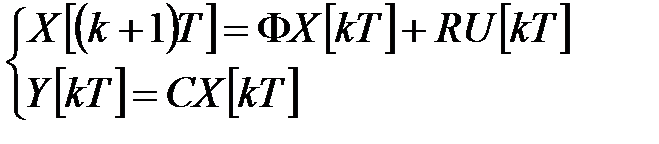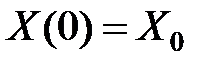(8)
Решение уравнений (8) может быть получено следующим образом. Придавая индексу 
значения 
, 
, 
, 
, 
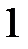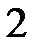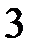, запишем:
;
= 
= 
=
;
= 
.
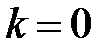
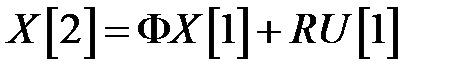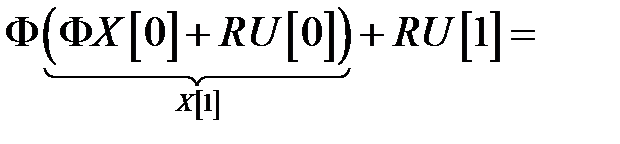
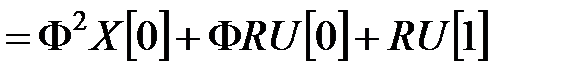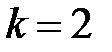
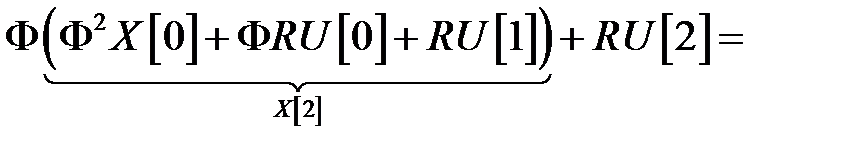
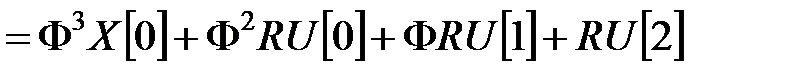В общем случае, при произвольном 
, имеем
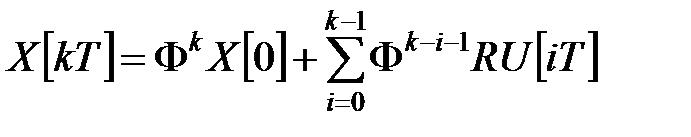(9)
Это общее решение первого уравнения (8).
Первое слагаемое (9) зависит только от начальных условий и определяет реакцию системы, не зависящую от входного (управляющего) воздействия 
. Это слагаемое называется свободной составляющей
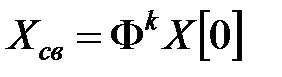(10)
Второе слагаемое (9) зависит только от значений 
, 
,..., 
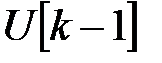и называется вынужденной составляющей
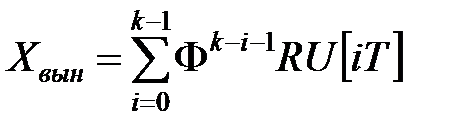. (11)
Замечание. Матрица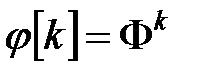 
называется переходной матрицей состояния дискретной системы или фундаментальной матрицей.
Для рассматриваемой в предыдущей части модели дискретной системы управления построим график изменения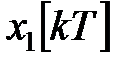 
, 
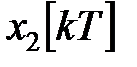на отрезке времени k=0, 1, 2, …, 10 для 
.
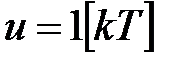С целью построения дискретного процесса определяем значения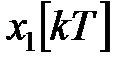 
, 
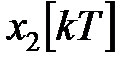, которые сводим в таблицу:
По полученным значениям построим графики
Список литературы
1. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов. – М.: Радио и связь, 1990. – 256 с.
2. Иванов В.А., Ющенко А.С. Теория дискретных систем автоматического управления. - М.: Наука, 1983.
3. Рабинер П., Гоулд Б. Теория и применение цифровой обработки сигналов. – М.: Мир, 1978. – 848 с.
4. Ройтенберг Я.Н. Автоматическое управление. – М.: Наука, 1978. – 552 с.
5. Теория автоматического управления / Под ред. А.В.Нетушила. – М.: Высшая школа, 1976. – 432 с.
6. Юревич Е.И. Теория автоматического управления. – Л.:Энергия,1975.– 412 с.
