Лекция 9. Элементы регрессионного анализа
Парный линейный регрессионный анализ.
Пусть проводится наблюдение над двумерной г.с. (Х, Y).
Если фиксировать значение x случайной величины X, то можно рассмотреть условное математическое ожидание с.в. Y при X = x: M [ Y / X = x ]. Таким образом, M [ Y / X = x ] является некоторой детерминированной функцией от x: M [ Y / X = x ] = j (x). Эта функция называется функцией регрессии Y на X, а график функции y = j (x) кривой регрессии Y на X. Если наблюдаетя с.в. Y при определенных значениях x, то случайную величину Y можно представить в виде Y = j (x)+ e, где e – с.в. Пусть наблюдения проводятся при фиксированных значениях x 1, x 2, …, xn. При этом случайная величина Y приняла соответственно значения y 1, y 2, …, yn. Тогда можно считать, что имеет место выборка yi = j (xi) + ei, i =1, …, n. В дальнейшем будем считать, что случайные величины e i, i =1, …, n, удовлетворяют следующим условиям.
1) ei (i =1, …, n) распределены по нормальному закону с математическим ожиданием 0 и дисперсией s 2;
2) они попарно некоррелированны.
Если функция регрессии j (x) линейна, то говорят, что имеет место линейная регрессионная модель. Рассмотрим подробно эту модель.
Пусть Y = b 0+ b 1 x + e, y i= b 0+ b 1 xi + ei, (i =1, …, n) и выполняются условия 1) – 2).
Задача корреляционного и регрессионного анализа состоит в следующем.
1) Получить наилучшие точечные и интервальные оценки параметров b 0, b 1, s линейной модели;
2) Проверить значимость модели;
3) Проверить адекватность модели наблюдаемым данным.
Для нахождения точечных оценок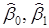 
применяется метод наименьших квадратов (сокращенно – МНК).
Обозначим искомое уравнение 
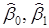. По МНК коэффициенты ищут, такие, чтобы принимала минимальное значение сумма
,
где обозначено 
.
По необходимому условию экстремума частные производные функции S по переменным 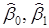должны обратиться в нуль в точке минимума.
Итак, решаем систему
Преобразовав систему, получаем
(9.1)
По методу Крамера, получим
,
где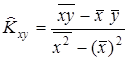 
– выборочный корреляционный момент, 
– выборочная дисперсия с.в. X.
Преобразовав далее, получим
,
где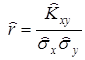 
– выборочный коэффициент корреляции.
В итоге получаем формулы для оценок коэффициентов уравнения линейной регрессии:
, 
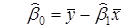. (9.2)
Коэффициент 
называется выборочным коэффициентом регрессии. Выборочное уравнение регрессии имеет вид 
Введем в рассмотрение следующие суммы.
– сумма квадратов отклонений,
– остаточная сумма квадратов,
– сумма квадратов, обусловленная регрессией,
называется остаточной дисперсией.
Теорема 9.1 
.
Если параметр 
= 0, то линейная модель называется незначимой. Для проверки значимости линейной модели выдвигается основная гипотеза H0: = 0 при альтернативной гипотезе H1: ¹ 0.
Статистика 
имеет распределение Фишера с 1 и n–2 степенями свободы, если основная гипотеза верна. Таким образом, если выборочное значение Fв больше квантили 
распределения Фишера, то основная гипотеза отвергается с вероятностью a, то есть на уровне значимости a линейная модель статистически значима.
Доверительные интервалы для коэффициентов , 
c доверительной вероятностью 1– a имеют вид:
< 
< 
,
< 
< 
,
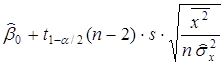где 
– квантиль распределения Стьюдента порядка 1– a./ 2 со степенью свободы n–2.
Коэффициентом детерминации называется величина 
. Чем ближе значение коэффициента детерминации к 1, тем лучше линейная модель описывает наблюдаемые данные. Если имеет место линейная регрессионная модель, то выборочный коэффициент корреляции между X, Y 
.
