Дискретные двумерные случайные величины.
Пусть Х, Y – две дискретные случайные величины, имеющие следующие законы распределения соответственно:
pi ·= P (X = xi) (x 1< x 2< …), p · j = P (Y = yj) (y 1< y 2< …), 
.
Двумерная с.в. (Х, Y) называется дискретной двумерной случайной величиной (или дискретно распределенной двумерной случайной величиной).
Закон распределения двумерной дискретной с.в. может быть задан в виде функции 
, где 
.
Если с.в. Х принимает конечное множество значений x 1, x 2, …, xn, а Y – конечное множество значений y 1, y 2, …, ym , то закон распределения задают обычно в виде таблицы 6.1. В этой таблице
, 
.
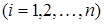Заметим, что первая и последняя строки таблицы 6.1 задают закон распределения с.в. Y, а первый и последний столбцы – закон распределения с.в. Х.
Таблица 6.1
| y 1 | y 2 | ××× | ym | å | |
| x 1 | p 11 | p 12 | ××× | p 1 m | 
|
| x 2 | P 21 | p 22 | ××× | p 1 m | 
|
| ××× | ××× | ××× | ××× | ××× | ××× |
| xn | pn 1 | pn 1 | ××× | Pnm | 
|
| å |  
| 
| ××× | 
|
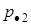
Непрерывно распределенные двумерные случайные величины
Если функция распределения F (x, y)непрерывна и существует такая неотрицательная интегрируемая функция р (x, y), что выполняется равенство
, (6.1)
то двумерная с.в. (Х, Y) называется непрерывно распределенной двумерной с.в. (или непрерывной двумерной с.в.). Функция р (x, y) называется плотностью распределения двумерной с.в. (Х, Y).
Равенство (6.1) позволяет по плотности распределения найти функцию распределения. Следовательно, закон распределения двумерной с.в. может быть задан как при помощи функции распределения, так и при помощи плотности распределения.
Плотность распределения непрерывной двумерной с.в.
Свойства плотности распределения.
1) р (x, y) ³ 0;
2) свойство нормировки 
;
3) 
, если р (x, y) непрерывна в точке (x, y);
4) 
, 
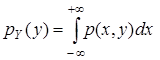, где 
– плотности одномерных с.в. Х и Y соответственно;
5) 
, где D – множество на плоскости, имеющая площадь.
Формула 5 означает, что вероятность попадания двумерной с.в. в область D равна двойному интегралу от плотности.
Первое свойство следует из определения плотности распределения.
Свойство нормировки следует из того, что
.
Третье свойство следует из формулы (6.1) по правилу дифференцирования интеграла по верхнему пределу интегрирования.
Четвертое свойство следует из следующей цепочки равеннств:
.
Пятое свойство примем без доказательства.
Независимость двух случайных величин.
Случайные величины Х, Y называются независимыми, если
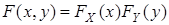для всех x, y.
Из этого равенства следует, что непрерывные с.в. Х, Y являются независимыми в том и только в том случае, когда 
для всех x, y.
Две дискретные случайные величины Х, Y являются независимыми в том и только в том случае, когда 
для всех i, j.
