Условная вероятность
Пусть имеется вероятностное пространство (W, U, P). Рассмотрим два события A и B, причем P (B)>0.
Определение. Условной вероятностью события A при условии, что событие B произошло, называется число
. (2.1)
Условную вероятность еще обозначают PB (A). Фактически условная вероятность при условии выполнения события В рассматривается в новом вероятностном пространстве, где “комплексу условий проведения опыта” (см. начало п.1.1) добавляется еще одно условие, что событие В произошло. Тогда новое пространство элементарных событий будет подмножеством W, алгебра событий и вероятности изменятся.
Пример. Рассмотрим опыт К1 событие А – “выпало число, большее трех“. Вероятность Р (А) = 3/6 = 1/2. Пусть событие В – “выпало четное число” произошло. Тогда пространством элементарных событий в новых условиях является {2, 4, 6}. Вероятность события А при условии, что событие B произошло, равно по классическому определению вероятности 2/3, так как число всех элементарных событий в новом пространстве элементарных событий равно 3 и два элементарных события 4 и 6 благоприятствуют событию А. Теперь эту условную вероятность вычислим по определению:
В = {2, 4, 6} Þ Р (В) = 3/6 = 1/2; AB = {4, 6} Þ Р (АВ) = 2/6 = 1/3.
.
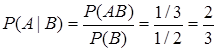Как видно, результаты совпали.
Независимость событий.
Определение. Два события A и B называются (вероятностно) независимыми, если
Р (АВ) = Р (А) Р (В) (2.2)
Пусть P (B)>0, A и B независимы. Тогда в силу равенства (2.2) выполняется равенство 
. Из этого следует, что если события A и B независимы, то вероятность Р (А) не зависит от того, произошло ли событие В или нет.
В теории вероятности применяется принцип: если события А и В причинно независимы, то они независимы вероятностно.
Докажите утверждение: если события А и В независимы, то независимы пары событий А и 
, В и 
.
Теперь определим понятие независимости нескольких событий.
Определение. События A 1, A 2 , …, Аn (n ³ 2) называются независимыми (в совокупности), если для любого сочетания по k (2 £ k £ n) из этих событий выполняется равенство
.
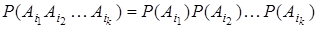Формула умножения вероятностей.
Если события A 1, A 2 , …, Аn (n ³ 2) независимы, то из определения независимости следует формула умножения вероятностей
.
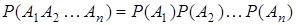Эта формула читается так: вероятность произведения нескольких независимых событий равна произведению их вероятностей и носит название формулы умножения вероятностей.
Теперь рассмотрим формулу вероятности произведения событий для произвольных событий. Из формулы (2.1) следует
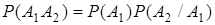(2.3)
Обобщение этой формулы для n (n ³ 2) событий приводит к формуле
.
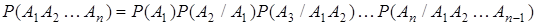Формула полной вероятности
Пусть для событий H 1, H 2 , …, Hn (n ³ 2) выполнены два условия:
1) они попарно несовместны и имеют ненулевые вероятности;
2) 
.
Тогда верна формула полной вероятности:
(2.4)
События H 1, H 2 , …, Hn называются гипотезами, а смысл равенства состоит в том, что событие А может произойти только с одним из гипотез.
Выведем эту формулу. Так как события АНi (i = 1, …, n) несовместны, то по формуле сложения вероятностей и формуле (2.3) имеем
,
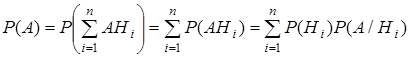что и требовалось доказать.
Задача 2.1 В магазин поступили однотипные телевизоры с 1-го завода 10 шт., со 2-го завода 15 шт. Вероятность изготовить бракованный телевизор на 1-м заводе равна 0,1, на 2-м – 0,2. Случайно отобрали один из поступивших телевизоров. Какова вероятность того, что он бракованный?
Решение. Введем события:
А – «Выбранный телевизор оказался бракованным»,
Н 1– «Выбранный телевизор изготовлен на 1-м заводе»,
Н 2– «Выбранный телевизор изготовлен на 2-м заводе»,
Гипотезы Н 1, Н 2 несовместны и событие А может произойти только с одним из них. Значит можно применить формулу полной вероятности.
P(Н 1)=10/25 = 2/5=0,4; P(A/ Н 1) = 0,1;
P(Н 2)=15/25 = 3/5=0,6; P(A/ Н 2) = 0,2.
Формула Байеса
При выполнении для гипотез H 1, H 2 , …, Hn и события А условий 1) и 2) п. 2.3 верна формула Байеса:
, i = 1, …, n. (2.5)
По этим формулам вычисляются так называемые апостериорные вероятности гипотез, то есть вероятности гипотез после того как событие А произошло. Безусловные вероятности гипотез Р (Нi) называются априорными.
Задача 2.2 При условиях задачи из 2.1 найти вероятность гипотез Н 1, Н 2 ,если известно, что отобранный телевизор оказался бракованным.
Решение. Используя результаты вычислений из решения задачи 2.1, по формуле Байеса имеем:
Как видим, апостериорная вероятность гипотезы Н 1 уменьшилась по сравнению априорной вероятностью. Объяснение простое: поскольку на первом заводе брака делается в два раза меньше, чем на втором, а выбранный телевизор оказался бракованным, то, естественно, вероятность того, что он из 1-го завода уменьшится.
Схема и формула Бернулли
Схема Бернулли – это независимое многократное повторение одного и того же опыта, который имеет два противоположных события: успех и неудача.
Введем обозначения:
p – вероятность успеха,
q = 1– p – вероятность неудачи,
n – число повторения опыта (n ³ 2),
k – число успехов в n повторениях опыта (k = 0,1, …, n).
Вероятность появления k раз успеха в n независимых повторениях опыта вычисляется по формуле Бернулли:
, (2.6)
где 
– число сочетаний из n по k.
Вывод формулы Бернулли. Результатом n независимых повторений опыта является произведение n успехов и неудач в совокупности: 
, где 
– либо успех, либо неуспех. Если в этом произведении k успехов и n–k неудач, то по формуле умножения вероятностей
.
Два события вида , имеющие ровно k успехов отличаются тем, что успехи располагаются на разных местах. Если выписать подряд номера мест, соответствующие успехам, то получим сочетание из n по k. Таким образом, событий вида , имеющих ровно k успехов, ровно 
. Следовательно, по формуле сложения вероятностей
,
где суммирование осуществляется по всем событиям вида , имеющим ровно k успехов.
Пример 2.1. Пятикратное подбрасывание монеты является схемой Бернулли с параметрами n = 5, p =0.5, q = 0.5. По формуле Бернулли
Пример 2.2. В аппаратуре работают независимо 1000 однотипных элементов. Вероятность выхода каждого из них за время работы T равна p = 0.005. Эту ситуацию можно рассматривать как схему Бернулли с n = 1000, p =0.005, q = 0.995. Обратите внимание на то, что успехом здесь является “негативное” событие – “Элемент вышел из строя за время работы T ”.
По формуле Бернулли 
Нетрудно понять, что вычисление этого выражения затруднительно. Поэтому необходимы приближенные формулы для вычисления вероятностей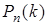 
.
