Теория вероятностей и математическая статистика
лекции
для студентов 2–3 курсов
ШАХТЫ 2003
Лекция 1
Пространство элементарных событий
При построении вероятностной модели в теории вероятностей всегда подразумевается, что рассматривается некоторый опыт. Опыт понимается в широком смысле: опыт, который поставил сам человек, опыт в смысле наблюдения над каким-то природным или социальным явлением и т.п. От опыта требуется следующее условие: он в принципе может быть повторен многократно примерно при одинаковых условиях (при выполнении некоторого комплекса условий проведения опыта).
Пример 1.1. Опыт К1 – игральный кубик бросается один раз. Этот опыт можно повторить многократно, при этом кубик можно бросать на одну и ту же поверхность, примерно на одинаковую высоту и т.д.
Пример 1.2. Опыт ЧК – подсчет числа обращений клиентов в сервисный центр по ремонту бытовой техники фирмы SONY. Комплекс условий предполагает, что подсчет производится за определенный промежуток времени (например за один месяц), рассматривается конкретный сервисный центр (например, головной сервисный центр в г. Ростове-на-Дону) и социально-экономическая ситуация стабильна.
Пример 1.3. Опыт ВБР – наблюдение над временем безотказной работы телевизора (время безотказной работы – это время первого отказа при беспрерывной работе аппаратуры). Комплекс условий проведения опыта и многократность здесь состоит в том, что опыт производится с несколькими однотипными телевизорами одновременно.
Под элементарным событием понимается в некотором смысле «элементарный» результат опыта. Элементарность результата понимается в том смысле, что его нельзя “составить” из других результатов опыта. Основное требование к элементарному событию состоит в том, чтобы в результате проведения опыта происходило одно и только одно элементарное событие.
В опыте К1 элементарным событием является, например, “выпало число 3”. Таким образом, в этом опыте имеются шесть элементарных событий: “выпало число k ”, k =1, 2, …, 6. Для сокращения событие “выпало число k ” обозначим числом k.
В опыте ЧК элементарным событием является “число обращений равно k ”, где k = 0, 1, 2, …. Это элементарное событие обозначим неотрицательным целым числом k.
В опыте ВБР элементарным событием можно считать t, где t – любое неотрицательное действительное число.
В дальнейшем считается, что опыт зафиксирован и все рассмотрения производятся в рамках этого опыта.
Множество всех элементарных событий (опыта) называется пространством элементарных событий и оно обозначается буквой W (омега).
В примере 1 W = {1, 2, 3, 4, 5, 6}, в опыте ЧК W = {0, 1, 2, 3, … }, в опыте ВБР W = [0, +¥).
Если пространство элементарных событий W является конечным или счетным, то пространство называется дискретным.
Пространства элементарных событий из примеров 1 и 2 являются дискретными, пространство из примера 3 не является дискретным.
События и действия (операции) над ними.
Событием является подмножество пространства элементарных событий W. При этом, если W дискретное, то любое его подмножество является событием. Если W не является дискретным, то не всякое подмножество является событием. В этом случае вводится понятие алгебры событий, которые подчиняются некоторым определенным свойствам. События обозначаются большими латинскими буквами с индексами или без них. Например, в опыте К1 событие А “выпало четное число” равно {2, 4, 6}.
Определение. Говорят, что произошло событие А, если результате опыта произошло элементарное событие, входящее в А.
Так как само множество W Ì W и пустое множество Æ Ì W, то они являются событиями. Событие W называется достоверным, если оно происходит обязательно. Событие Æ называется невозможным, оно не произойдет никогда, так как не содержит ни одного элементарного события. Если событие А отлично от W и Æ, то невозможно до опыта наверняка предугадать, произойдет оно или нет. Поэтому события в теории вероятностей называются случайными.
Суммой двух событий А и В называется событие, которое происходит в том и только в том случае, когда происходит хотя бы одно из событий А, В. Сумма обозначается А + В. Таким образом, А + В = А È В (объединение множеств А и В)
Произведением двух событий А и В называется событие, которое происходит в том и только в том случае, когда происходит и событие А и событие В. Произведение обозначается АВ. Таким образом, АВ = А Ç В (пересечение множеств А и В).
Разностью между событиями А и В называется событие, которое происходит в том и только в том случае, когда происходит событие А, но не происходит событие В. Разность обозначается А – В. Таким образом, А – В = А \ В (разность между множествами А и В).
Событие W – А называется противоположным событием событию А и обозначается  .
.
Очевидно, А происходит в том и только в том случае, когда противоположное ему событие  не происходит.
не происходит.
События А и В называются несовместными, если они не могут произойти вместе. Это значит, что АВ = Æ.
Говорят, что из события А следует событие В (или событие А влечет событие В), если из того, что событие А произошло следует что и событие В произошло. Этот факт обозначается А Ì В или А Þ В.
Рассмотрим опыт К1. Пусть А – “выпало четное число”, В – “выпало простое число”. А = {2, 4, 6}, В = {2, 3, 5}. А + В = {2, 3, 4, 5, 6}, АВ = {2}, А – В = {4, 6},
 = {1, 3, 5}. События А и
= {1, 3, 5}. События А и  несовместны.
несовместны.
Замечание. Операции сложения, умножения событий, понятие несовместности можно определить для трех, четырех и т.д. событий.
Свойства операций над событиями.
| 1) А+В = В+А | 2) АВ=ВА |
| 3) А+А = А | 4) АА=А |
| 5) А+ W = W | 6) А W = А |
| 7) А+Æ = А | 8) АÆ = Æ |
| 9) (А+В)С=АС+ВС | 10) АВ+С=(А+С)(В+С) |
11) 
| 12) 
|
13) A + 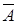 =W =W
| 14) A 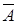 = Æ = Æ
|
Свойства 11 и 12 называются правилами де Моргана.




