Обработка результатов опытов

Цель работы

1. Углубление знаний по теории теплоотдачи при свободном движении.

2. Усвоение методики опытного исследования теплоотдачи и обработки результатов.

3. Развитие навыков в проведении эксперимента.

При выполнении данной работы должны быть усвоены: понятия и сущность теплоотдачи, свободного движения, закон Ньютона – Рихмана,

сущность коэффициента теплоотдачи и его зависимость от различных факторов, методика экспериментального определения коэффициента теплоотдачи, понятие о теории подобия, числах и уравнениях подобия конвективного теплообмена.

 

Задание

1. Определить коэффициент теплоотдачи при свободном движении воздуха около вертикальной трубы и установить зависимость от температурного напора.

2. Полученные в опытах величины коэффициента теплоотдачи сравнить с вычисленными по уравнению подобия.

3. Составить отчёт по выполненной работе.

 

Методика определения коэффициента теплоотдачи

Процесс конвективного теплообмена между поверхностью твердого тела и соприкасающейся с ней жидкостью (или газом) называется теплоотдачей.

Этот процесс осуществляется одновременно теплопроводностью и конвекцией и неразрывно связан с движением жидкости (газа).

Движение жидкости или газа, возникающее вследствие разности плотностей нагретых и холодных частиц, называется свободным движением.

Количество переносимой теплоты в единицу времени – тепловой поток Q _К, Вт, при теплоотдаче определяется по закону Ньютона – Рихмана:

 

Q _K = F (t_C – t_Ж) = F t,

где

F – поверхность теплообмена, м²;

 

t = t_C – t_Ж - температурный напор, ;

t_C – температура поверхности стенки, ;

t_Ж – температура жидкости или газа, ;

- коэффициент теплоотдачи, Вт/(м² К).

 

Опытным путём коэффициент теплоотдачи можно определить по закону Ньютона – Рихмана:

 

.

Следовательно, для определения α по этой формуле при опытах необходимо знать тепловой поток конвективного теплообмена Q _K, поверхность теплообмена F, её среднюю температуру t_C и температуру жидкости (газа) t _Ж.

 

Схема опытной установки.

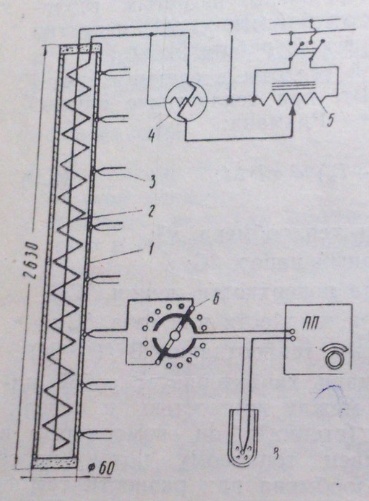d = 50 мм

h = 2630 мм

= 0,5

1-вертикальная дюралевая труба.

2- электронагреватель в виде спирали.

3- медь-константановые термопары, 8 шт.

4-ваттметр класса 0,5.

5-лабораторный автотрансформатор.

 

 

Журнал наблюдений.

 

№ опыта	№ замера	Температура, °С	Средняя температура поверхности, tc, °С	Температура воздуха,   tж, °С	Мощность эл. двигателя, W, Вт
1-й опыт			50,5	50,3	50,7	50,5	49,5	49,8		50,4		I=1,43A U=100B W=143Bт
		50,8	50,5	50,8	50,3		49,8	49,4	50,2
		50,8	50,6		50,6	49,9		49,5	50,3
2-й опыт		60,1	61,3	60,1	61,5	60,5	59,1	59,2	59,3	60,6		I=1,73A U=125B W=216Вт
	60,4	61,8	61,4	61,7	59,8	59,9	59,9	59,8	60,6
	60,7		61,5	61,8	61,2		59,9	59,9	60,6
3-й опыт				70,2		69,3	67,8	67,9	67,6	69,1		I=1,87A U=136B W=255Bт
	68,1	71,5	70,5	71,5			67,8	67,5	69,2
	68,3				69,6				69,6

 

 

Обработка результатов опытов

Расчёт для 1-го опыта:

Коэффициент теплоотдачи от поверхности трубы вычисляется по формуле:

 

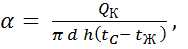Вт/(м² ∙ К) (1),

где

d и h – диаметр и высота исследуемой трубы, м;

d h – её поверхность теплообмена, м²;

t_C – средняя температура поверхности, ° С­;

t_Ж – температура окружающего воздуха, С.

Тепловой поток, передаваемый от поверхности трубы к воздуху путём конвективного теплообмена, определяется как разность

 

Q_K = Q – Q_Л, Вт (2),

 

 

где

Q – полный тепловой поток, Q =W;

W – мощность, потребляемая электронагревателем.

Тепловой поток, передаваемый излучением от поверхности трубы к окружающим её телам, определяется по уравнению

 

 

Q_Л = F ₁, Вт (3),

 

Здесь с₀ – излучательная способность абсолютно черного тела;

с ₀ = 5,67 Вт/(м² ∙ К⁴).

F ₁ = d h – поверхность трубы, м²;

Т ₁ = t _С + 273 – средняя абсолютная температура поверхности трубы, К;

Т ₂ = t _Ж + 273 – абсолютная температура окружающих тел, принимаемая равной температуре воздуха, К;

_П – приведены коэффициент теплового излучения системы тел.

 

F ₁ = 3,14 ∙ 0,05 ∙ 2,63 = 0,412 м²

 

Т ₁ = 50,3 + 273 = 323 К

 

Т ₂ = 19 + 273 = 292 К

 

 

Q_Л = ∙ 0,412 = 46,44 Вт

 

Q _К = 143 – 46,44 = 96,56 Вт

 

 

= 7,47 Вт/(м² ∙ К).

 

P _r = - число Прандтля, характеризующее физические свойства жидкости;

α = 21,27 ∙ 10^-6, м²/с, (табл.) - коэффициент температуропроводности;

ν = 14,97 ∙ 10^-6, м²/с, (табл.) – кинематический коэффициент вязкости.

P _r = 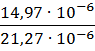= 0,704

G _r = 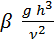(4),

где

G _r - число Грасгофа, характеризующее подъёмную силу, возникающую в жидкости вследствие разности плотностей;

- коэффициент объёмного расширения, 1/К, определяется по формуле:

 

= 1 / (t _ж +273), (5),

 

= 1 / (19 + 273) = 0,0034;

g – ускорение свободного падения, м/с²,

= t _{С ­} - t _Ж - температурный напор, ° С

= 50,3 – 19 = 31,3 ° С

 

G _r = 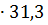= 8,4 ∙ 10¹⁰

G_rЖ ∙ Р _rЖ = 0,704 ∙ 8,4 ∙ 10¹⁰ = 5,9 ∙ 10¹⁰

Для турбулентного режима

Nu _Ж = 0,15 (G_rЖ ∙ Р _rЖ )^0,33

Nu _Ж = 0,15 ∙ (5,9 ∙ 10¹⁰)^0,33 = 538

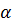= Nu _Ж , Вт/(м² ∙ К), (6),

где λ = 0,0258 Вт/(м² ∙ К) – коэффициент теплопроводности (табл.).

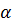= 538 ∙ = 5,27 Вт/(м² ∙ К)

 

Расчёт для 2-го опыта:

 

= 60,6 – 19 = 41,6 ° С

 

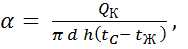Вт/ (м² ∙ К)

 

Q_Л = F ₁, Вт

 

 

F ₁ = 0,412 м²

 

Т ₁ = 60,6 + 273 = 333,6 К

 

Т ₂ = 19 + 273 = 292 К

 

Q =W = 216 Вт,

Q_Л = ∙ 0,412 = 65,65 Вт

 

Q _К = 216 – 65,65 = 150,35 Вт

 

 

= 8,75 Вт/(м² ∙ К).

 

P _r = - число Прандтля, характеризующее физические свойства жидкости;

α = 21,27 ∙ 10^-6, м²/с, (табл.) - коэффициент температуропроводности;

ν = 14,97 ∙ 10^-6, м²/с, (табл.) – кинематический коэффициент вязкости.

P _r = 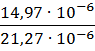= 0,704

G _r = 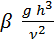– число Грасгофа, характеризующее подъёмную силу, возникающую в жидкости вследствие разности плотностей;

где

- коэффициент объёмного расширения, 1/К, определяется по формуле:

 

= 1 / (t _ж +273),

 

= 1 / (19 + 273) = 0,0034;

g – ускорение свободного падения, м/с²,

= t _{С ­} - t _Ж - температурный напор, ° С

= 41,6 ° С

 

G _r = = 11,2 ∙ 10¹⁰

G_rЖ ∙ Р _rЖ = 0,704 ∙ 11,2 ∙ 10¹⁰ = 7,8 ∙ 10¹⁰

Для турбулентного режима

Nu _Ж = 0,15 (G_rЖ ∙ Р _rЖ )^0,33

Nu _Ж = 0,15 ∙ (7,8 ∙ 10¹⁰)^0,33 = 589

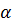= Nu _Ж , Вт/(м² ∙ К),

где λ = 0,0258 Вт/(м² ∙ К) – коэффициент теплопроводности (табл.).

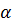= 589 ∙ = 5,77 Вт/(м² ∙ К)

 

 

Расчёт для 3-го опыта:

 

= 69,3 – 19 = 50,3 ° С

 

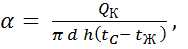Вт/(м² ∙ К)

 

Q_Л = F ₁, Вт

 

 

F ₁ = 0,412 м²

 

Т ₁ = 69,3 + 273 = 342,3 К

 

Т ₂ = 19 + 273 = 292 К

 

Q =W = 255 Вт,

Q_Л = ∙ 0,412 = 83 Вт

 

Q _К = 255 – 83 = 172 Вт

 

 

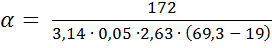= 8,28 Вт/(м² ∙ К).

 

P _r = - число Прандтля, характеризующее физические свойства жидкости;

α = 21,27 ∙ 10^-6, м²/с, (табл.) - коэффициент температуропроводности;

ν = 14,97 ∙ 10^-6, м²/с, (табл.) – кинематический коэффициент вязкости.

P _r = 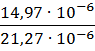= 0,704

G _r = 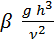– число Грасгофа, характеризующее подъёмную силу, возникающую в жидкости вследствие разности плотностей;

где

- коэффициент объёмного расширения, 1/К, определяется по формуле:

 

= 1 / (t _ж +273),

 

= 1 / (19 + 273) = 0,0034;

g – ускорение свободного падения, м/с²,

= t _{С ­} - t _Ж - температурный напор, ° С

= 69,3 ° С

 

G _r = = 18,5 ∙ 10¹⁰

G_rЖ ∙ Р _rЖ = 0,704 ∙ 18,5 ∙ 10¹⁰ = 13,024 ∙ 10¹⁰

Для турбулентного режима

Nu _Ж = 0,15 (G_rЖ ∙ Р _rЖ )^0,33

Nu _Ж = 0,15 ∙ (13,024 ∙ 10¹⁰)^0,33 = 698

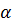= Nu _Ж , Вт/(м² ∙ К),

где λ = 0,0258 Вт/(м² ∙ К) – коэффициент теплопроводности (табл.).

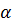= 698 ∙ = 6,84 Вт/(м² ∙ К)

 

 

Результаты расчёта

 

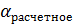№ Опыта	Вт/(м2 ∙ К)	Вт/(м2 ∙ К)
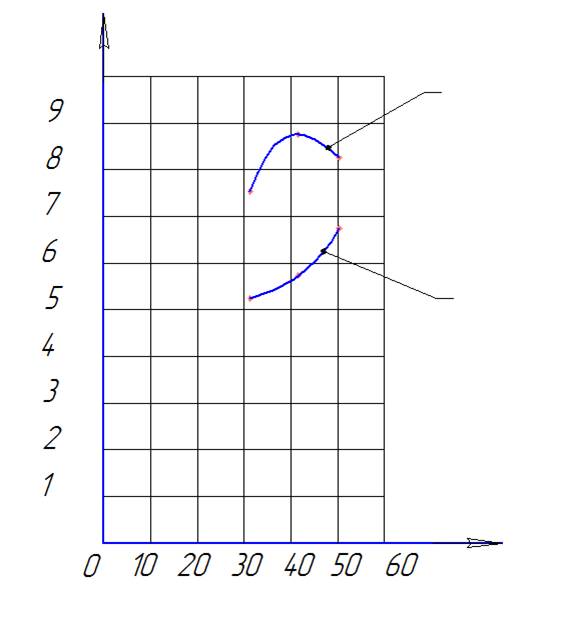
	7,47	5,27	31,3
	8,75	5,77	41,6
	8,28	6,84	50,3

 

График зависимостей по эксперементу и по расчёту.