Направление: Юриспруденция
Дисциплина: Математические методы
Анализа и принятия решений
Преподаватель: Егорова Н.Н.
Контрольная работа для студентов заочного отделения*.
Раздел 1. Основания математики.
1. Дано: А – множество натуральных чисел первого десятка, кратных трем;
В – множество четных натуральных чисел первого десятка;
С – множество простых натуральных чисел первого десятка;
D – множество нечетных натуральных чисел первого десятка.
Требуется: а) задать указанные множества перечислением элементов;
б) найти множество Х;
в) найти множество Y.
| Вариант | Задание множества Х | Задание множества Y |

| Y – множество всех двухэлементных подмножеств Х | |

| 
| |

| Y – булеан множества Х | |

| 
| |

| 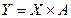
| |

| Y – множество всех трехэлементных подмножеств Х | |

| Y - множество всех четырехэлементных подмножеств Х | |

| 
| |

| Y – булеан множества Х | |

| 
|
2. Составить таблицу истинности для формулы логики высказываний:
| Вариант | Формула логики | Вариант | Формула логики | |

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
|
Раздел 2. Элементы теории вероятностей и математической статистики.
3,4. Решить задачи в соответствии со своим вариантом:
| Вариант №1 3) В данный район изделия поставляются тремя фирмами в соотношении 5:8:7. Среди продукции первой фирмы стандартные изделия составляют 90%, второй — 85%, третьей — 75%. Найти вероятность того, что приобретенное изделие оказалось стандартным. 4) Торговый агент имеет 5 телефонных номеров потенциальных покупателей и звонит им до тех пор, пока не получит заказ на покупку товара. Вероятность того, что потенциальный покупатель сделает заказ, равна 0,4. Составить закон распределения числа телефонных разговоров которые предстоит провести агенту. Найти математическое ожидание и дисперсию этой случайной величины. | Вариант №2 3) Предполагается, что 10% открывающихся новых малых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из шести малых предприятий не более двух в течение года прекратят свою деятельность? 4) Каждый поступающий в институт должен сдать 3 экзамена. Вероятность успешной сдачи первого экзамена 0,9, второго — 0,8, третьего — 0,7. Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего. Составить закон распределения числа экзаменов, сдававшихся поступающим в институт. Найти математическое ожидание этой случайной величины. |
| Вариант №3 3) В группе из 10 студентов, пришедших на экзамен, 3 подготовлено отлично, 4 — хорошо, 2 — посредственно и 1 — плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все, 20 вопросов, хорошо подготовленный — на 16, посредственно — на 10, плохо — на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что студент подготовлен отлично. 4) Из 10 телевизоров на выставке 4 оказались фирмы «Сони». Наудачу для осмотра выбрано 3. Составить закон распределения числа телевизоров фирмы «Сони» среди 3 отобранных. | Вариант №4 3) В коробке смешаны электролампы одинакового размера и формы: по 100 Вт — 7 штук, по 75 Вт — 13 штук. Вынуты наудачу 3 лампы. Какова вероятность того, что они одинаковой мощности? 4) Охотник, имеющий 4 патрона, стреляет по дичи до первого попадания или до израсходования всех патронов. Вероятность попадания при первом выстреле на 0,6, при каждом последующем — уменьшается на 0,1. Необходимо составить закон распределения числа патронов, израсходованных охотником и найти математическое ожидание и дисперсию этой случайной величины. |
| Вариант №5 3) В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы три договора. 4) Найти закон распределения числа пакетов трех акций, по которым владельцем будет получен доход, если вероятность получения дохода по каждому из них равна соответственно 0,5, 0,6, 0,7, Найти математическое ожидание и дисперсию данной случайной величины. | Вариант №6 3) Мастер обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания рабочего, равна 0,3, второй — 0,6, третий — 0,4 и четвертый — 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера. 4) Среди 15 собранных агрегатов 6 нуждаются в дополнительной смазке. Составить закон распределения числа агрегатов, нуждающихся в дополнительной смазке, среди пяти наудачу отобранных из общего числа. |
| Вариант №7 3) Учебник издан тиражом 10 000 экземпляров. Вероятность того, что экземпляр учебника сброшюрован неправильно, равна 0,0001. Найти вероятность того, что по крайней мере 9998 книг сброшюрованы правильно. 4) Имеются 4 ключа, из которых только один подходит к замку. Составить закон распределения числа попыток открывания замка, если испробованный ключ в последующих попытках не участвует. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины. | Вариант №8 3) Страховая компания разделяет застрахованных по классам риска: I— малый риск, II— средний, III — большой риск. Среди этих клиентов 50% — I класса риска, 30% —II и 20% — III. Вероятность необходимости выплачивать страховое вознаграждение для I класса риска равна 0,01, для II — 0,03, для III — 0,08. Какова вероятность того, что получивший денежное вознаграждение застрахованный относится к группе малого риска? 4) Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения числа библиотек, которые посетит студент если в городе 4 библиотеки. Найти математическое ожидание и дисперсию этой случайной величины |
| Вариант №9 3) Студент знает 20 из 25 вопросов программы. Зачет считается сданным, если студент ответит не менее чем на 3 из 4 поставленных в билете вопросов. Какова вероятность того, что студент сдаст зачет? 4) Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,2. За каждое попадание он получает 5 очков, а в случае промаха очков ему начисляют. Составить закон распределения числа очков, полученных стрелком за 3 выстрела, и вычислить математическое ожидание этой случайной величины. | Вариант №10 3) Студент разыскивает формулу в трех справочниках. Вероятность того, что формула содержится в 1-м, 2-м и 3-м справочниках, равна соответственно 0,6, 0,7 и 0,8. Найти вероятность того, что эта формула содержится не менее, чем в двух справочниках. 4) Вероятность поражения вирусным заболеванием куста земляники равна 0,2. Составить закон распределения числа кустов земляники, зараженных вирусом, из четырех посаженных кустов. Найти математическое ожидание и дисперсию этой случайной величины. |
*Каждый студент должен выполнить задания своего варианта, номер варианта определяется по последней цифре номера зачетной книжки студента (последняя цифра перед дробной чертой). Если последняя цифра номера зачетки 1, то студент выполняет задания варианта №1; цифрой 2 – вариант №2 и т.д., если номер зачетки заканчивается цифрой 0 – вариант №10.
При оформлении работы необходимо для каждой задачи привести полное условие с данными своего варианта, решение с необходимыми пояснениями, ясный ответ.






