Предположим, что преподаватель задал n=18 (совершеннолетие).
Задание №1. Так как n=18, то N=180. Составим таблицу данных (группировочную таблицу):
| значения измеряемого признака | xi | |||||
| частота | ni |
1.1.Для нахождения числовых характеристик рекомендуем воспользоваться формулами таблицы 1 для сгруппированных данных:
Среднее арифметическое 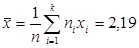 , где
, где  .
.
Медиана 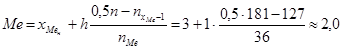 , в нашем случае
, в нашем случае  ,
,  ,
,  ,
, 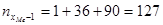 ,
, 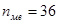 .
.
Мода  , при этом
, при этом  ,
,  ,
,  .
.
Дисперсия 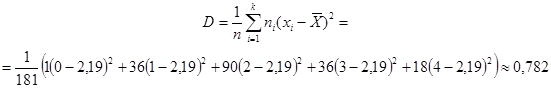
Стандартное отклонение 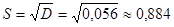 .
.
Коэффициент вариации 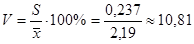 .
.
1.2. Если выборка нормально распределена, то 99,9 % данных лежат в интервале  , в нашем случае
, в нашем случае 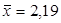 ,
,  , таким образом мы будем рассматривать интервал
, таким образом мы будем рассматривать интервал 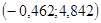 . Очевидно, что все данные выборки принадлежат рассматриваемому интервалу, поэтому можем считать выборку нормально распределенной.
. Очевидно, что все данные выборки принадлежат рассматриваемому интервалу, поэтому можем считать выборку нормально распределенной.
1.3. Графически данная выборка может быть представлена следующим образом: 
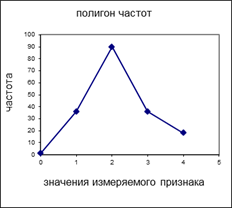

Задание №2. n=18, N=180. Заполним исходную таблицу данных:
| выборка X | ||||||||||
| выборка Y | 18,5 | 19,5 | 19,5 | 19,5 |
2.1. Решение подобного упражнения рассмотрено на занятии №5.
1.1.1. Примем предположение о нормальности распределения выборок. В качестве нулевой гипотезы Н0 примем предположение о равенстве дисперсий рассматриваемых выборок, тогда альтернатива Н1 – предположение о том, что дисперсии не равны. Уровень значимости a=0,05
1.1.2. Найдем средние значения  и
и  . Они равны:
. Они равны: 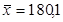 ,
, 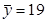 .
.
1.1.3. Найдем значения выборочных дисперсий:  ,
, 
1.1.4. Видим, что  >
> 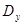 . Обозначим
. Обозначим 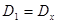 ,
,  .
.
1.1.5. Вычисляют значение F-критерия по формуле: 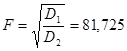 .
.
1.1.6. Критическое значение F кр=3,2. Так как F>F кр, то делаем вывод о том, что дисперсии различаются значимо на уровне значимости a=0,05.
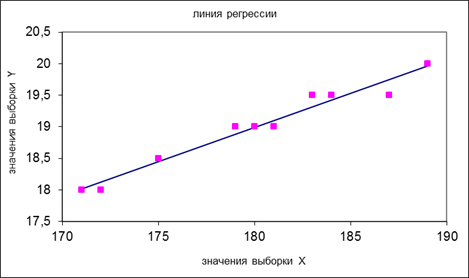
1.2. Нахождение коэффициента корреляции и построение линии регрессии рассматривалось на занятии №8.
Для вычисления коэффициента корреляции составляют расчетную таблицу:
| № п/п | X | Y | X2 | Y2 | XY |
| 18,5 | 342,25 | 3237,5 | |||
| 19,5 | 380,25 | 3568,5 | |||
| 19,5 | 380,25 | ||||
| 19,5 | 380,25 | 3646,5 | |||
| СУММЫ | 34254,5 |
Коэффициент корреляции рассчитывают по формуле:
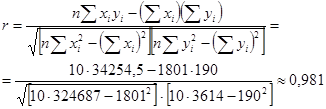
Вычисленное значение позволяет сделать вывод о сильной статистической связи между величинами X и Y.
1.3. Вычислим коэффициенты регрессии: b =0,109, a =-0,558. Уравнение регрессии тогда примет вид y =0,109 x -0,558. Для построения прямой регрессии достаточно знать две точки, которые ей принадлежат. Одна из этих точек – (180,1;19) – ее координатами являются средние значения рассматриваемых выборок. Вторую достаточно легко найти, подставив произвольное значение величины Х в уравнение регрессии. Возьмем, например, х =190, тогда y =20,15. Итак, второй точкой будет (190;20,15)
Задание №3. Прежде всего, составим таблицу исходных значений (n=18, N=126):
| до эксперимента | X | |||||||||||
| после эксперимента | Y | |||||||||||
| разности | d | -1 | -1 |
3.1. В данном случае применяется критерий Стъюдента для связанных выборок (занятие №5):
1.1.1. Делается предположение о нормальном распределении разностей 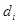 , формулируются H0:
, формулируются H0:  и H1:
и H1: 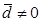 , выбирается уровень значимости a=0,05.
, выбирается уровень значимости a=0,05.
1.1.2. Вычисляются среднее арифметическое  и выборочное стандартное отклонение
и выборочное стандартное отклонение  .
.
1.1.3. Определяют значение t-критерия по формуле: 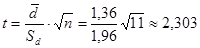 .
.
1.1.4. По таблице находим критическое значение при уровне значимости a=0,05: t кр=2,228.
1.1.5. Делаем вывод: т.к.  , то наблюдаемое различие значимо на уровне значимости a.
, то наблюдаемое различие значимо на уровне значимости a.
3.2. Применение непараметрических критериев рассматривалось на занятии №6.
После того как отбросим пары с одинаковыми значениями данная таблица примет вид:
| X | |||||||||
| Y | |||||||||
| d | -1 | -1 | |||||||
| ранги |
Находим суммы рангов R(-)=6, R(+)=39. Так как сумма R(-)<R(+), то в качестве критерия Вилкоксона W принимаем R(-). Итак, W=6. Критическое значение Wкр=5. Так как, W> Wкр, то можем сделать вывод о том, что в результате эксперимента произошло изменение измеряемой величины.






