Построение спирали Архимеда.

Спираль Архимеда- плоская кривая линия, которую описывает точка, движущаяся равномерно вращающемуся радиусу.

Для построения спирали Архимеда задают ее шаг P, из центра О проводят окружность радиусом, равным шагу P спирали, и делят шаг и окружность на несколько равных частей. Точки деления нумеруют.

Из центра О проводят радиальные прямые, проходящие через точки деления окружности.

Из центра О радиусами О1, О2 и т.д. проводят дуги до пересечения с соответствующими радиальными прямыми. Например, дуга радиуса О3 пересекается с прямой О31 в точке III. Полученные точки I, II,...,VIII, принадлежащие спирали Архимеда, соединяют плавной кривой по лекалу.

В машиностроении спираль Архимеда применяется, например, для сообщения движения в радиальном направлении кулачкам зажимного патрона токарного станка. На тыльной стороне большой конической шестерни нарезаны канавки по спирали Архимеда. В канавки входят выступы кулачков, которые также выполнены по спирали. При вращении шестерни кулачка будут перемещаться в радиальном направлении.

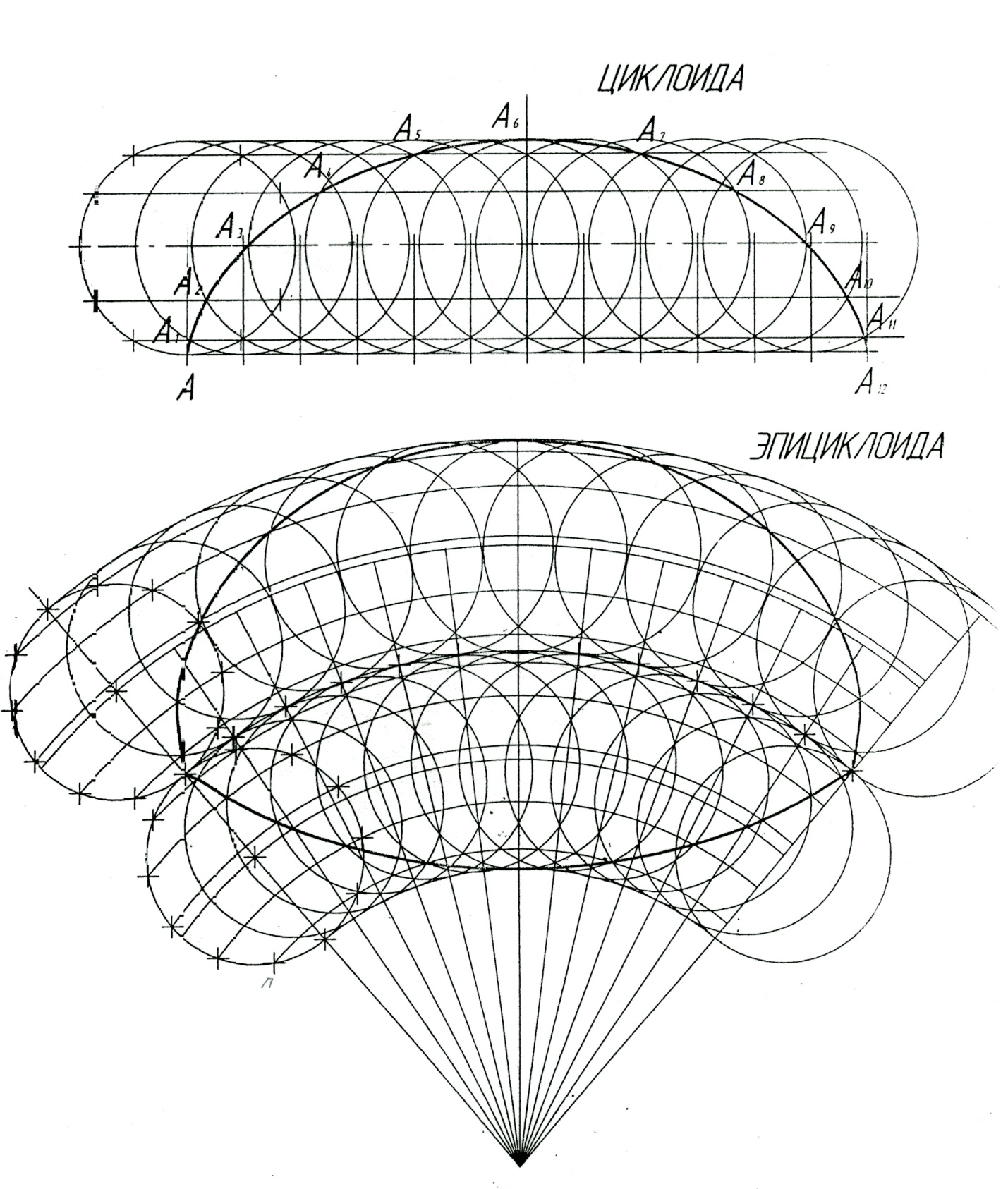
Циклоидой называется плоская кривая, описываемая точкой, которая катится без скольжения по прямой линии. Для построения циклоиды проводим прямую СВ и на ней отмечаем точку А - начало движения окружности заданного диаметра. В точке А восставляем перпендикуляр и на нем откладываем радиус или заданный диаметр данной окружности. Из полученной точки О заданным радиусом описываем окружность, которую делим на равные части, например на 12. На прямой СВ от точки А откладываем длину окружности πD, которую делим на то же число равных частей.

Через точки деления 1, 2, 3,..., 12 на окружности проводим линии, параллельные СВ. Линия, проходящая через центр окружности О, будет центровой линией ОО12. Из точек деления 1, 2, 3,..., 12 на прямой СВ восставляем перпендикуляры до центровой линии, точки пересечения О1, О2,..., О12 - положение центров окружности в различные моменты движения. Из этих точек описываем окружности заданного радиуса. В точках пересечения этих окружностей с линиями, проведенными из точек деления окружности в первоначальном ее положении, параллельными СВ, получим точки, принадлежащие кривой циклоиды, соединив которые между собой по лекалу, получим кривую, называемую циклоидой.

Гипоциклоидой называется кривая, описываемая точкой окружности, которая катится без скольжения по внутренней стороне дуги неподвижной окружности. Катящаяся окружность называется производящей, а дуга - направляющей.

Построим гипоциклоиду - по заданному радиусу R, направляющей дуги и диаметру D производящей окружности. Из точки О как из центра радиусом R проводим направляющую дугу. Определяем произвольный центральный угол â=180d/R и из точки О проводим два луча ОА и ОВ. Из точки О0 проводим центральную линию производящей окружности радиусом R=ОО0. Эта линия пересечет лучи, проходящие через точки А и В, в точках О0 и О12. Из центра О0 проводим производящую окружность диаметром D и делим ее, например на двенадцать частей, отмечая точки деления. Дугу АВ делим на такое же число равных частей и тоже отмечаем все точки. Из точки О через точки деления О1,...О12 проводим лучи до пересечения с линией центров, а через точки деления 1...12 производящей окружности проводим вспомогательные дуги.

Пересечения вспомогательных дуг с производящей окружностью при ее движении дадут искомые точки, соединив которые плавной кривой по лекалу, получим кривую, называемую гипоциклоидой.

Эпициклоидой называется плоская кривая, которую описывает точка окружности при ее качении без скольжения по наружной стороне дуги неподвижной окружности. Если обозначить диаметр производящей окружности через D, радиус направляющей дуги через R, а центральный угол охвата эпициклоиды через â, то â=180D/R. Построение эпициклоиды производиться аналогично построению гипоциклоиды.

Тема Аксонометрические проекции. Стандартные виды аксонометрии. Аксонометрические проекции плоских фигур и геометрических тел. Аксонометрические проекции окружностей. Аксонометрические проекции построения деталей Графическая работа № 6. Построение прямоугольной изометрии и диметрии детали. Формат А3 (420 × 297).