Комплексная контрольная работа по разделу «Теоретическая механика» включает три задания:
- задание С1 по теме «Статика»;
- задание К1 по теме «Кинематика»;
- задание Д3 по теме «Динамика».
К каждой задаче дается 10 рисунков и таблица (с тем же номером, что и задача), содержащая дополнительные к тексту задачи условия. Нумерация рисунков двойная, при этом номером рисунка является цифра, стоящая после точки. Например, рис. С1.4 - это рис. 4 к задаче С1 и т.д. (в тексте задачи при повторных ссылках на рисунок пишется просто рис. 4 и т.д.). Номера условий от 0 до 9 проставлены в 1-м столбце (или в 1-й строке) таблицы.
Студент во всех задачах выбирает номер рисунка по предпоследней цифре шифра, а номер условия в таблице - по последней; например, если шифр оканчивается числом 46, то берет рис. 4 и условия № 6 из таблицы.
Задания выполняются в отдельной тетради (ученической), страницы которой нумеруются. На обложке указываются: название дисциплины, фамилия и инициалы студента, учебный шифр, факультет, специальность и адрес, если работа высылается по почте.
Решение каждой задачи обязательно начинать на развороте тетради (на четной странице, начиная со второй). Сверху указывается номер задачи, далее делается чертеж (можно карандашом) и записывается, что в задаче дано и что требуется определить (текст задачи не переписывать). Чертеж выполняется с учетом условий решаемого варианта задачи; на нем все углы, действующие силы, число тел и их расположение на чертеже должны соответствовать этим условиям. В результате в целом ряде задач чертеж получится более простой, чем общий.
Чертеж должен бытьаккуратным и наглядным, а его размеры должны позволять ясно показать все силы или векторы скорости и ускорения и др.; необходимо обязательное изображение на чертеже всех вычисляемых векторов и координатных осей, а также указание единиц получаемых размерных величин. Решение задач необходимо сопровождать краткими пояснениями (какие формулы или теоремы применяются, откуда получаются те или иные результаты и т.п.) и подробно излагать весь ход расчетов. На каждой странице следует оставлять поля для замечаний рецензента.
Работы, не отвечающие всем перечисленным требованиям, проверяться не будут и будут возвращаться для переделки.
К работе, предъявляемой на повторную проверку (если она выполнена в другой тетради), должна обязательно прилагаться незачтенная работа. На экзамене необходимо представить зачтенные по данному разделу курса работы, в которых все отмеченные погрешности должны быть исправлены.
При чтении текста каждой задачи учесть следующее. Большинство рисунков дано без соблюдения масштаба. На рисунках к задачам С1 все линии, параллельные строкам, считаются горизонтальными, а перпендикулярные строкам - вертикальными и это в тексте задач специально не оговаривается. Также без оговорок считается, что все нити (веревки, тросы) являются нерастяжимыми и невесомыми, нити, перекинутые через блок, по блоку не скользят, катки и колеса (в динамике) катятся по плоскостям без скольжения. Все связи, если не сделано других оговорок, считаются идеальными.
Когда тела на рисунке пронумерованы, то в тексте задачи и в таблице Р 1, l 1, r 1 и т.п. означают вес или размеры тела 1, P 2, l 2, r 2 - тела 2 и т.д. Аналогично в кинематике и динамике  обозначают скорость и ускорение точки В,
обозначают скорость и ускорение точки В, 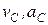 - точки С;
- точки С;  - угловую скорость и угловое ускорение тела 1,
- угловую скорость и угловое ускорение тела 1,  - тела 2 и т.д. В каждой задаче подобные обозначения могут тоже специально не оговариваться.
- тела 2 и т.д. В каждой задаче подобные обозначения могут тоже специально не оговариваться.
Следует также иметь в виду, что некоторыеиз заданных в условиях задачи величин (размеров) при решении каких-нибудь вариантов могут не понадобиться, они нужны для решения других вариантов задачи. Из всех пояснений в тексте задачи обращайте внимание только на относящиеся к вашему варианту, т.е. к номеру вашего рисунка или вашего условия в таблице.
Методические указания по решению задач, входящих в контрольные задания, даются для каждой задачи после изложения ее текста под рубрикой "Указания"; затем дается пример решения аналогичной задачи. Цель примера - разъяснить ход решения, но не воспроизвести его полностью. Поэтому в ряде случаев промежуточные расчеты опускаются. Но при выполнении задания все преобразования и числовые расчеты должны быть обязательно последовательно проделаны с необходимыми пояснениями; в конце должны быть даны ответы.
СТАТИКА
Задание С1
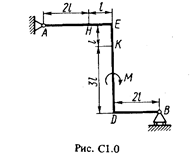
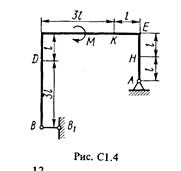
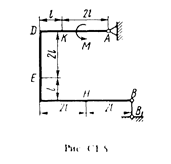
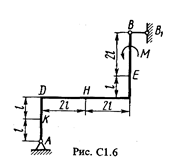
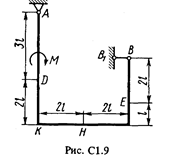
Жесткая рама (рис. С1.0-С1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню ВВ1, или к шарнирной опоре на катках; стержень прикреплен к раме и к неподвижной опоре шарнирами.
| 
|

| 
|
| 
|
| 
|

| 
|
Таблица С1
| Сила | 
| 
| 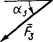
| 
| ||||
| Номер условия | F1 = 10 H | F2 = 20 H | F3 = 30 H | F4 = 40 H | ||||
| Точка прилож. | 
| Точка прилож. | 
| Точка прилож. | 
| Точка прилож. | 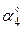
| |
| - | - | D | E | - | - | |||
| K | - | - | - | - | H | |||
| - | - | H | K | - | - | |||
| D | - | - | - | - | E | |||
| - | - | K | E | - | - | |||
| H | - | - | D | - | - | |||
| - | - | E | - | - | K | |||
| D | - | - | H | - | - | |||
| - | - | H | - | - | D | |||
| T | - | - | - | - | K |
На раму действуют пара сил с моментом М = 100 Н×м и две силы, значения которых, направления и точки приложения указаны в таблице (например, в условиях № 1 на раму действуют сила F1 = 10 Н под углом 30° к горизонтальной оси, приложенная в точке К, и сила F4 =40 Н под углом 60° к горизонтальной оси, приложенная в точке Н).
Определить реакции связей в точках А и В, вызываемые заданными нагрузками. При окончательных подсчетах принять l = 0,5 м.
Указания. Задача C1 - на равновесие тела под действием плоской системы сил. Составляя уравнения равновесия, учесть, что уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей (в данном случае относительно точки А). При вычислении момента силы  часто удобно разложить ее (согласно аксиоме параллелограмма сил) на составляющие
часто удобно разложить ее (согласно аксиоме параллелограмма сил) на составляющие  и
и  (не обязательно параллельно координатным осям), так, чтобы плечи этих составляющих определялись легче, чем плечо силы
(не обязательно параллельно координатным осям), так, чтобы плечи этих составляющих определялись легче, чем плечо силы  . После этого воспользоваться теоремой Вариньона в алгебраической форме:
. После этого воспользоваться теоремой Вариньона в алгебраической форме:
 .
.
Пример C1. Жесткая пластина ABCD (рис. C1) имеет в точке А неподвижную шарнирную опору, а в точке В - подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.

| Дано: F = 25 кН, a = 60°, Р = 18 кН, g = 75°, М = 50 кН × м, b =30°, l = 0,5 м. Определить: реакции в точках А и В, вызываемые действующими нагрузками. |
Решение
1. Рассмотрим равновесие пластины. Проведем координатные оси ху и изобразим действующие на пластину силы: силу  , пару сил с моментом М, натяжение троса
, пару сил с моментом М, натяжение троса  (по модулю Т = Р) и реакции связей
(по модулю Т = Р) и реакции связей  (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
(реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
2. Для полученной плоской системы сил составим три уравнения равновесия. При вычислении момента силы  относительно точки А воспользуемся теоремой Вариньона, т.е. разложим силу
относительно точки А воспользуемся теоремой Вариньона, т.е. разложим силу  на составляющие
на составляющие  и учтем, что
и учтем, что  . Получим
. Получим
 (1)
(1)

 (2)
(2)
 (3)
(3)
Начинаем с уравнения (3), так как там одна неизвестная  :
:

 кН.
кН.
Подставляем  в уравнение (1):
в уравнение (1):
 кН.
кН.
Подставляем  в уравнение (2):
в уравнение (2):
 кН.
кН.
Проверка. Составим, например, уравнение  (или уравнение моментов относительно любой другой точки (кроме А). Если задача решена верно, то эта сумма моментов должна быть равна нулю.
(или уравнение моментов относительно любой другой точки (кроме А). Если задача решена верно, то эта сумма моментов должна быть равна нулю.


Ответ: ХА = -8,5 кН, YA = -23,3 кН, RB = 7,3 кН. Знаки указывают, что силы  и
и  направлены противоположно показанным на рис. C1.
направлены противоположно показанным на рис. C1.
КИНЕМАТИКА
Задание К1
Точка В движется в плоскости ху (рис. К1.0-К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1 (t), у = f2 (t), где х и у выражены в сантиметрах, t -в секундах.
Найти уравнение траектории точки; для момента времени t1, = 1с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х = f1, (t) указана непосредственно на рисунках, а зависимость у = f2 (t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4). Как и в задаче C1 номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 - по последней.
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются касательное и нормальное ускорения точки.
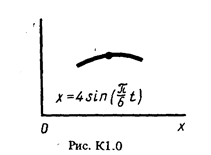
| 
|
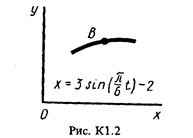
| 
|

| 
|

| 
|

| 
|
Таблица К1
| Номер условия | y = f2 (t) | ||
| Рис. 0-2 | Рис.3-6 | Рис.7-9 | |

| 
| 
| |

| 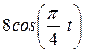
| 
| |

| 
| 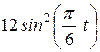
| |

| 
| 
| |

| 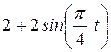
| 
| |
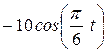
| 
| 
| |

| 
| 
| |

| 
| 
| |

| 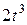
| 
| |

| 
| 
|
В данной задаче все искомые величины нужно определить только для момента времени t1 = 1 с. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы: cos 2a= 1 - 2sin2a = 2 cos2a- 1; sin 2a = 2sin a×cos a.
Пример К1.
Уравнения движения точки в плоскости имеют вид:
 , (1)
, (1)
 , (2)
, (2)
где время t задано в секундах, координаты x, y - в метрах.
Найти:
1. уравнение траектории точки;
2. положение точки на траектории при  (начальное положение) и при
(начальное положение) и при  c;
c;
3. скорость  точки;
точки;
4. ускорение  точки;
точки;
5. касательное  , нормальное
, нормальное  ускорения точки и радиус кривизны траектории
ускорения точки и радиус кривизны траектории 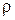 .
.
В каждом пункте выполнить соответствующие построения на рисунке.
Решение
Движение точки задано координатным способом.
1. Найдем уравнение траектории, исключив из (1) и (2) параметр t - время. Способ исключения t зависит от вида функций в правых частях (1), (2). В данном случае найдем из (1), (2) соответственно
 .
.
Возводя полученные соотношения в квадрат, после этого складывая их и учитывая, что  , найдем:
, найдем:

Из этого уравнения следует, что траекторией точки является эллипс, полуоси которого равны 4 м и 6 м, а центр имеет координаты (0, 0).
Выберем масштаб длин и выполним рисунок. Следует заметить, что приведенный рис. 1 имеет вид, соответствующий уже окончанию решения; свой рисунок рекомендуется делать по мере продвижения решения. Это позволяет контролировать получаемые результаты и делает их более наглядными. Данное замечание относится и ко всем последующим задачам пособия.
2. Находим положение точки при  , подставляя это значение t в (1) и (2):
, подставляя это значение t в (1) и (2):
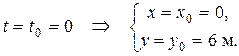
3. Находим положение точки при 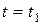 , подставляя это значение t в (1) и (2):
, подставляя это значение t в (1) и (2):

Указываем на рисунке точки  и
и  , учитывая масштаб координат.
, учитывая масштаб координат.
4. Найдем скорость точки. Из теории следует, что при координатном способе задания движения определяются сначала проекции скорости на оси координат. Используя (1) и (2) - уравнения движения точки - находим
 , (3)
, (3)
 . (4)
. (4)
Модуль скорости 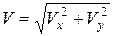 . Подставляя сюда (3), (4), получим
. Подставляя сюда (3), (4), получим
 . (5)
. (5)
При  с:
с:  ,
,  ,
,
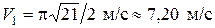 . (6)
. (6)
 Рис. 1
Рис. 1
| Выберем масштаб для скоростей (рис.1), проведем в точке M 1 линии парал-лельные осям x и y, и на этих линиях в масштабе скоростей отложим отрезки: 5,44 по оси x и - 4,71 по оси y, что соответствует величи-нам и знакам найденных проекций скорости. На этих составляющих строим пара-ллелограмм (прямоуголь-ник), диагональ которого по величине и направлению соответствует вектору  .
Проверьте следующее: длина построенного вектора должна получиться равной найденному значению .
Проверьте следующее: длина построенного вектора должна получиться равной найденному значению 
|
(с учетом масштаба скоростей). Вектор  направлен по касательной к траектории в точке
направлен по касательной к траектории в точке  и показывает направление движения точки по траектории.
и показывает направление движения точки по траектории.
Удобно сейчас построить в точке  естественные оси: касательную
естественные оси: касательную  и главную нормаль
и главную нормаль  (они потребуются позже). Касательную
(они потребуются позже). Касательную  проводим вдоль
проводим вдоль  ; главную нормаль
; главную нормаль  проводим перпендикулярно
проводим перпендикулярно  в плоскости рисунка и направляем к центру кривизны траектории в точке
в плоскости рисунка и направляем к центру кривизны траектории в точке  (в сторону вогнутости траектории).
(в сторону вогнутости траектории).
5. Находим ускорение точки, используя (3), (4):
 , (7)
, (7)
 . (8)
. (8)
Модуль ускорения  . Из (7), (8) получим
. Из (7), (8) получим
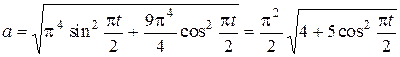 . (9)
. (9)
Подставляя в (7) - (9)  , найдем
, найдем
 ,
,  ,
,
 . (10)
. (10)
В точке  строим в масштабе проекции ускорений
строим в масштабе проекции ускорений  , учитывая их величины и знаки, а затем строим вектор ускорения
, учитывая их величины и знаки, а затем строим вектор ускорения  . Построив
. Построив  , следует проверить, получилось ли на рисунке
, следует проверить, получилось ли на рисунке  (c учетом масштаба ускорений), и направлен ли вектор
(c учетом масштаба ускорений), и направлен ли вектор  в сторону вогнутости траектории (вектор
в сторону вогнутости траектории (вектор  проходит через центр эллипса, но это есть особенность данной задачи, связанная с конкретным видом функций (1) и (2)).
проходит через центр эллипса, но это есть особенность данной задачи, связанная с конкретным видом функций (1) и (2)).
6. Находим касательное ускорение  , характеризующее изменение модуля
, характеризующее изменение модуля  .
.
Учитывая (5), получим 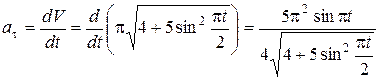 .
.
При 
 . (11)
. (11)
Касательное ускорение можно также найти, дифференцируя по времени равенство 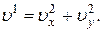 Получим
Получим
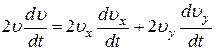 , откуда следует
, откуда следует

Нормальную составляющую  ускорения, характеризующую изменение направления
ускорения, характеризующую изменение направления  , можно найти по формуле
, можно найти по формуле
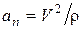 , (12)
, (12)
если 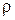 - радиус кривизны траектории заранее известен, или (учитывая, что,
- радиус кривизны траектории заранее известен, или (учитывая, что, 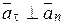 и, следовательно,
и, следовательно,  ) по формуле
) по формуле
 . (13)
. (13)
Так как в данной задаче радиус 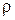 заранее неизвестен, то используем (13). Подставляя (10), (11) в (13), получим
заранее неизвестен, то используем (13). Подставляя (10), (11) в (13), получим
 . (14)
. (14)
Вернемся к рис. 1. Ранее на этом рисунке вектор  был построен по составляющим
был построен по составляющим  ,
,  . С другой стороны, этот вектор можно разложить на составляющие по естественным осям
. С другой стороны, этот вектор можно разложить на составляющие по естественным осям  и
и  (пользуясь правилом параллелограмма). Выполним это разложение и построим на рисунке векторы
(пользуясь правилом параллелограмма). Выполним это разложение и построим на рисунке векторы  и
и  . Полезно провести проверку: с учетом масштаба ускорений определить по рисунку величины
. Полезно провести проверку: с учетом масштаба ускорений определить по рисунку величины  ,
, 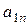 и убедиться, что они совпадают с (11), (14).
и убедиться, что они совпадают с (11), (14).
Заметим, что движение точки ускоренное, т.к. направления векторов  и
и 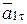 совпадают (рис. 1).
совпадают (рис. 1).
Найдем радиус кривизны 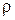 , используя (12), откуда следует, что
, используя (12), откуда следует, что  . Подставляя в последнее соотношение
. Подставляя в последнее соотношение  и
и 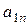 из (6) и (14), получим радиус кривизны траектории в точке
из (6) и (14), получим радиус кривизны траектории в точке  :
:  . Отложим на рисунке от точки
. Отложим на рисунке от точки  по оси
по оси  отрезок
отрезок 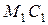 длины
длины 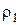 (в масштабе длин); полученная точка
(в масштабе длин); полученная точка  есть центр кривизны траектории в точке
есть центр кривизны траектории в точке  .
.
Объединяя полученные результаты, запишем ответ:
1. траектория точки - эллипс, имеющий уравнение  ;
;
2. 
3. 
4.  ;
;
5.  ;
;
6. 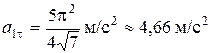 ;
;  ;
;
 .
.
Обсудим некоторые особенности и частные случаи, которые могут встретиться в задачах.
Если траектория точки - прямая линия, то  и, следовательно,
и, следовательно, 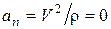 . Найденное по величине и направлению ускорение
. Найденное по величине и направлению ускорение  равно ускорению
равно ускорению  .
.
Если траектория точки - окружность, то  , где R - радиус окружности (определяется из уравнения траектории). Если скорость V точки найдена, то
, где R - радиус окружности (определяется из уравнения траектории). Если скорость V точки найдена, то  . Вектор
. Вектор  направлен к центру окружности. Касательное ускорение
направлен к центру окружности. Касательное ускорение  , полное ускорение
, полное ускорение  .
.
ДИНАМИКА
Задание Д3
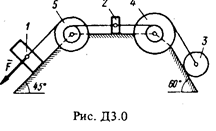
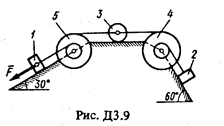
Механическая система состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость f = 0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R 4 = 0,3 м, r 4 = 0,3 м, R 5 = 0,3 м, r 5 = 0,3 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу) (рис. Д3.0 – Д3.9, табл. Д3). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям.
| 
|

| 
|

| 
|

| 
|

| 
|
Под действием силы F = f (s), зависящей от перемещения точки приложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивлений, равные соответственно M 4 и М 5.
Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы 
 равно s,. Искомая величина указана в столбце "Найти" таблицы, где обозначено:
равно s,. Искомая величина указана в столбце "Найти" таблицы, где обозначено:  - скорость груза 1,
- скорость груза 1, 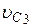 - скорость центра масс катка 3,
- скорость центра масс катка 3,  - угловая скорость тела 4 и т.д.
- угловая скорость тела 4 и т.д.
Таблица Д3
| Номер усло-вия | m 1, кг | m2, кг | m 3, кг | m 4, кг | m 5, кг | M 4, Н×м | M 5, Н×м | F = f(s) | s 1, м | Найти |
| 0,8 | 50(2+3 s) | 1,0 | 
| |||||||
| 0,6 | 20(5+2 s) | 1,2 | 
| |||||||
| 0,4 | 80(3+4 s) | 0,8 | 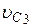
| |||||||
| 0,3 | 40(4+5 s) | 0,6 | 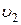
| |||||||
| 0,6 | 30(3+2 s) | 1,4 | 
| |||||||
| 0,9 | 40(3+5 s) | 1,6 | 
| |||||||
| 0,8 | 60(2+5 s) | 1,0 | 
| |||||||
| 0,6 | 30(8+3 s) | 0,8 | 
| |||||||
| 0,3 | 40(2+5 s) | 1,6 | 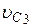
| |||||||
| 0,4 | 50(3+2 s) | 1,4 | 
|
Указания. Задача ДЗ - на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел: эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении кинетической энергии катка, совершающего плоское движение, для установления зависимости между его угловой скоростью и скоростью его центра масс воспользоваться понятием о мгновенном центре скоростей (кинематика). При определении работы все перемещения следует выразить через заданное перемещение s 1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
Когда по данным таблицы m 2 = 0, груз 2 на чертеже не изображать; шкивы 4 и 5 всегда входят в систему.
Пример ДЗ. Механическая система (рис. ДЗ) состоит из сплошного цилиндрического катка l, ступенчатого шкива 2 с радиусами ступеней R 2 и r 2 (масса шкива равномерно распределена по его внешнему ободу) и груза 3 (коэффициент трения груза о плоскость равен f). Тела системы соединены друг с другом нитями, намотанными на шкив 2.
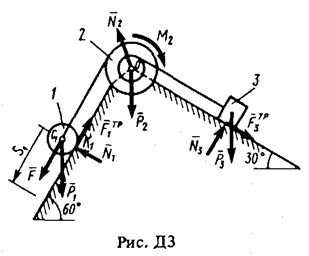
| Под действием силы F = f (s), зависящей от перемещения s точки ее приложения, система приходит в движения из состояния покоя. При движении на шкив 2 действует постоянный момент М 2 сил сопротивления.
Дано: m 1 = 4 кг, m 2 = 10кг,
m 3 = 8 кг, R 2 = 0,2 м, r 2 = 0,1м, f = 0,2. М 2 = 0,6 Н × м, F = 2(1+2 s) Н, s 1 = 2м.
Определить: скорость 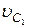 центра масс катка, когда s = s 1.
центра масс катка, когда s = s 1.
|
Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из тел 1 2, 3, соединенных нитями. Изобразим все действующие на систему внешние силы: активные 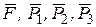 , момент сопротивления М 2 реакции
, момент сопротивления М 2 реакции  и силы трения
и силы трения  и
и 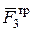 .
.
Для определения  воспользуемся теоремой об изменении кинетической энергии системы
воспользуемся теоремой об изменении кинетической энергии системы
 (1)
(1)
2. Определяем Т 0 и Т. Так как в начальный момент система находилась в покое, то Т 0 = 0. Величина Т равна сумме энергий всех тел системы:
 (2)
(2)
Учитывая, что тело 1 совершает плоское движение, тело 3 движется поступательно, а тело 2 вращается вокруг неподвижной оси, получим
 (3)
(3)
Все входящие сюда скорости следует выразить через искомую  . Приняв во внимание, что точка K 1 - мгновенный центр скоростей катка 1, и обозначив радиус катка через r 1, получим
. Приняв во внимание, что точка K 1 - мгновенный центр скоростей катка 1, и обозначив радиус катка через r 1, получим
 (4)
(4)
Кроме того, входящие в (3) моменты инерции имеют значения
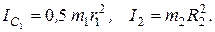 (5)
(5)
Подставив все величины (4) и (5) в равенство (3), а затем используя равенство (2) получим окончательно:
 (6)
(6)
3. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда точка С 1 пройдет путь s 1. Одновременно все перемещения следует выразить через заданную величину s 1, для чего учтем, что здесь зависимость между перемещениями будет такой же, как и между соответствующими скоростями в равенствах (4), т.е. 
 . В результате получим:
. В результате получим:


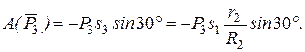
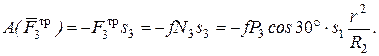
Работа остальных сил равна нулю, так как точка K 1, где приложены силы  и
и  , является мгновенным центром скоростей, точка O, где приложены
, является мгновенным центром скоростей, точка O, где приложены  , и
, и  , неподвижна, а реакция
, неподвижна, а реакция  перпендикулярна перемещению груза 3. Тогда окончательно
перпендикулярна перемещению груза 3. Тогда окончательно
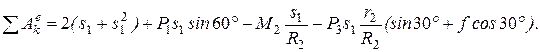 (7)
(7)
4. Подставив выражения (6) и (7) в уравнение (1) и учитывая, что T 0 = 0, получим

 (8)
(8)
При числовых значениях, которые имеют заданные величины, равенство (8) дает

Отсюда находим искомую скорость.
Ответ:  = 1.53м/с.
= 1.53м/с.






