ЗАДАНИЕ 1 Найти неопределенный интеграл
| Вариант | Интеграл | Вариант | Интеграл |
а)  б)
б) 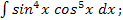 в)
в)  г)
г) 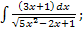 д)
д)  е)
е) 
| а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| ||
а)  б)
б)  в)
в)  г)
г) 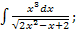 д)
д)  е)
е) 
| а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| ||
а)  б)
б)  в)
в) 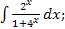 г)
г)  д)
д)  е)
е) 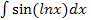
| а)  б)
б) 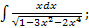 в)
в)  г)
г)  д)
д)  е)
е) 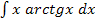
| ||
а)  б)
б)  в)
в)  г)
г) 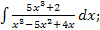 д)
д) 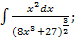 е)
е) 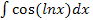
| а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| ||
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
|
ЗАДАНИЕ 2 Вычислить определенный интеграл
| Вариант | Интеграл | Вариант | Интеграл |
а)  б)
б)  в)
в) 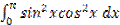
| а)  б)
б)  в)
в) 
| ||
а)  б)
б) 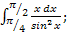 в)
в) 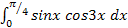
| а)  б)
б)  в)
в) 
| ||
а)  б)
б)  в)
в) 
| а)  б)
б)  в)
в) 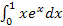
| ||
а)  б)
б)  в)
в) 
| а) 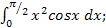 б)
б)  в)
в) 
| ||
а)  б)
б)  в)
в) 
| а)  б)
б)  в)
в) 
|
ЗАДАНИЕ 3 Вычислить площадь фигуры, ограниченной линиями
| Вариант | Уравнение линий | Вариант | Уравнение линий |
а)  б)
б) 
| а) 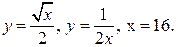 б)
б) 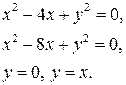
| ||
а)  б)
б) 
| а)  б)
б) 
| ||
а) 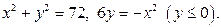 б)
б) 
| а)  б)
б) 
| ||
а)  б)
б) 
| а) 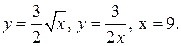 б)
б) 
| ||
а)  б)
б) 
| а) 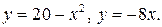 б)
б) 
|
ЗАДАНИЕ 4 Вычислить объем тела, ограниченного поверхностями
| Вариант | Уравнение поверхностей | Вариант | Уравнение поверхностей |

| 
| ||

|

| ||

| 
| ||

| 
| ||

| 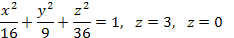
|
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
Основная литература:
1. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. - М.: Логос, 2004. - 184 с. + 1 эл. опт. диск (CD-ROM).
2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006. - 432 с.
3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2005. - 432 с.
4. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. - 4-е изд., стереотип. - М.: Дрофа, 2004. - 725 с.
5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. - 3-е изд., испр. - М.: ДРОФА, 2001. - 725 с.
6. Гурова, З.И. Высшая математика. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. - М.: Физматлит, 2002. - 351 с.
7. Высшая математика в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов. - 5-е изд., испр. - М.: ФИЗМАТЛИТ, 2002. - 479 с.
8. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учеб. для втузов. В 2 т. Т. 1 / Н.С.Пискунов. - Стер. изд. - М.: ИНТЕГРАЛ-ПРЕСС, 2004. - 415 с.
9. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учебник для втузов. В 2 т. Т. 2 / Н.С.Пискунов. - Стер. изд. - М.: ИНТЕГРАЛ-ПРЕСС, 2004. - 544 с.
10. Шипачев, В.С. Высшая математика: учеб. пособие для вузов / В.С.Шипачев. - М.: Высш. шк., 2002. - 176 с.
Дополнительная литература:
1. Босс, В. Лекции по математике: анализ. / В.Босс – М.: Едиториал УРСС, 2004 – 213с.
2. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П.Е.Данко [и др.]. - 7-е изд., испр. - М.: Оникс: Мир и Образование(М.), 2008. - 448 с.
3. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова, С.П.Данко. - 6-е изд. - М.: Оникс: Мир и Образование(М.), 2007. - 416 с.
4. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. - 6-е изд. - М.: Оникс: Мир и Образование(М.), 2005. - 416 с.
5. Задачи и упражнения по математическому анализу для втузов / Ред. Б.П.Демидович. – М.: АСТ-Астрель, 2004. - 495 с.
6. Кудрявцев, Л.Д. Краткий курс математического анализа: учеб. для вузов. В 2 т. Т. 2. Функции многих переменных / Л.Д.Кудрявцев. - 2-е изд., перераб. и доп. - Висагинас: Alfa, 1998. - 397 с.
7. Сборник задач и упражнений по математическому анализу. Ч.2 / С.И.Ляшко [и др.]; Ред. И.И. Ляшко. - М.; СПб.; Киев: Диалектика, 2001. - 430 с.
8. Стакун, А.А. Высшая математика: конспект лекций с решениями типовых примеров и метод. указ. к инд. заданиям (для студ.-заоч.). В 2 ч. Ч.2 / А.А.Стакун, С.И.Фролов. - СПб.: Политехника, 2001. - 147 с.
9. Цлаф, Л.Я. Вариационное исчисление и интегральные уравнения: справ. рук. / Л.Я.Цлаф. - 3-е изд., стереотип. – М.: Лань, 2005. - 191 с.
Вопросы к промежуточной аттестации
1. Понятие неопределенного интеграла. Свойства неопределенного интеграла. Таблица основных неопределенных интегралов.
2. Метод непосредственного интегрирования. Метод интегрирования подстановкой (заменой переменной). Метод интегрирования по частям.
3. Определение определенного интеграла как предел интегральной суммы, теорема Коши. Геометрический и физический смысл определенного интеграла: площадь криволинейной трапеции, работа переменной силы.
4. Формула Ньютона-Лейбница, свойства определенного интеграла.
5. Числовые ряды: определение, частичные суммы, сходимость, расходимость. Ряд геометрической прогрессии.
6. Необходимый признак сходимости числового ряда, гармонический ряд.
7. Признаки сравнения рядов: теорема о сравнении, предельный признак сравнения. Признак Даламбера.
8. Радикальный признак Коши. Интегральный признак Коши, обобщенный гармонический ряд.
9. Кратный интеграл. Вычисление кратного интеграла с помощью повторного интегрирования.
10. Криволинейные интегралы 1-го рода. Геометрический смысл.
11. Криволинейный интеграл 2-го рода. Физический смысл.
12. Формула Грина.
13. Поверхностный интеграл 1-го рода. Геометрический смысл.
14. Поверхностный интеграл 2-го рода. Физический смысл.
15. Формула Гаусса-Остроградского.
16. Формула Стокса.




