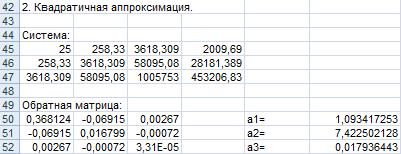
Рисунок 3
В ячейках A50:C52 записана формула {=МОБР(A45:C47)}.
В ячейках F50:F52 записана формула {=МУМНОЖ(A50:C52,D45:D47)}.
Теперь аппроксимируем функцию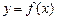 
экспоненциальной функцией 
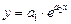. Для определения коэффициентов 
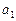и 
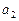прологарифмируем значения 
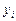и используя итоговые суммы из рисунка 2, расположенные в ячейках A26, C26, H26 и I26 получим систему:
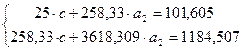
где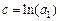 
.
Решив систему, найдем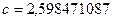 
, 
.
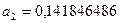После потенцирования получим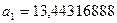 
.
Таким образом, экспоненциальная аппроксимация имеет вид
.
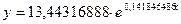Решение системы проводили, пользуясь средствами Microsoft Excel.
Результаты коэффициентов экспоненциальной аппроксимации.
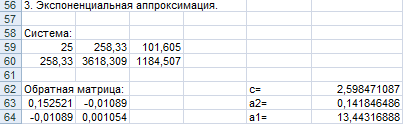
Рисунок 4
В ячейках A63:B64 записана формула {=МОБР(A59:B60)}.
В ячейках E62:E63 записана формула {=МУМНОЖ(A63:B64,C59:C60)}.
В ячейке E64 записана формула =EXP(E62).
Вычислим среднее арифметическое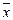 
и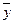 
по формулам:
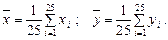
Результаты расчета 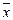и 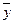средствами Microsoft Excel.
Вычисление средних значений X и Y.
Рисунок 5
В ячейке B66 записана формула =A26/25.
В ячейке B67 записана формула =B26/25.
Для того, чтобы рассчитать коэффициент корреляции и коэффициент детерминированности данные целесообразно расположить в виде рисунка 6, который является продолжением рисунка 1.
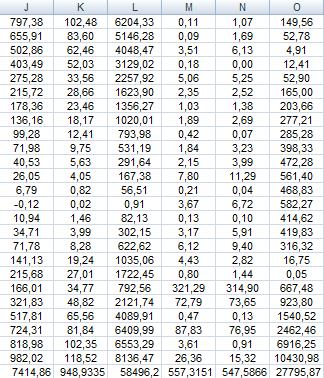
Рисунок 6
Шаг 1. В ячейку J1 вводим формулу =(A1-$B$54)*(B1-$B$55).
Шаг 2. В ячейки J2:J25 эта формула копируется.
Шаг 3. В ячейку K1 вводим формулу =(A1-$B$54)^2.
Шаг 4. В ячейки K2:K25 эта формула копируется.
Шаг 5. В ячейку L1 вводим формулу =(B1-$B$55)^2.
Шаг 6. В ячейки L2:L25 эта формула копируется.
Шаг 7. В ячейку M1 вводим формулу =($E$32+$E$33*A1-B1)^2.
Шаг 8. В ячейки M2:M25 эта формула копируется.
Шаг 9. В ячейку N1 вводим формулу
=($F$41+$F$42*A1+$F$43*A1^2-B1)^2.
Шаг 10. В ячейки N2:N25 эта формула копируется.
Шаг 11. В ячейку O1 вводим формулу
=($E$51*EXP($E$50*A1)-B1)^2.
Шаг 12. В ячейки O2:O25 эта формула копируется.
Шаг 13. В ячейку J26 вводим формулу =СУММ(J1:J25).
Шаг 14. В ячейку K26 вводим формулу =СУММ(K1:K25).
Шаг 15. В ячейку L26 вводим формулу =СУММ(L1:L25).
Шаг 16. В ячейку M26 вводим формулу =СУММ(M1:M25).
Шаг 17. В ячейку N26 вводим формулу =СУММ(N1:N25).
Шаг 18. В ячейку O26 вводим формулу =СУММ(O1:O25).
Теперь проведем расчеты коэффициента корреляции по формуле
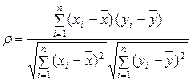(только для линейной аппроксимации)
и коэффициента детерминированности по формуле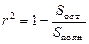 
.
Результаты расчета.
Рисунок 7
В ячейке В69 записана формула =J26/(K26*L26)^(1/2).
В ячейке B71 записана формула =1- M26/L26.
В ячейке B73 записана формула =1- N26/L26.
В ячейке B75 записана формула =1- O26/L26.
Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные.
Построение графиков
Для построения графиков я воспользуюсь мастером диаграмм Microsoft Excel. Для этого выделяю ячейки А1:В25, нажимаю кнопку «Вставка» ® «Диаграмма…» В появившемся окне задаю параметры диаграммы – вид диаграммы (точечная), её название, названия осей. После появления диаграммы, нажимаю правой кнопкой мыши непосредственно на одну из точек графика. В появившемся диалоговом окне выбираю команду «Добавить линию тренда». Появится меню, в котором я смогу выбрать способ автоматической аппроксимации и установить отображение уравнений.
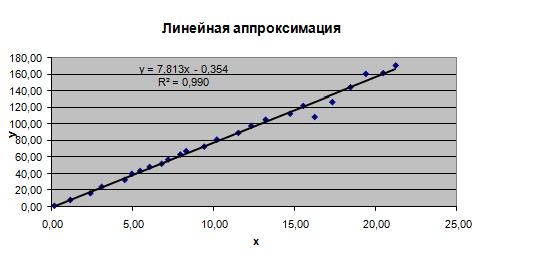
Рисунок 8
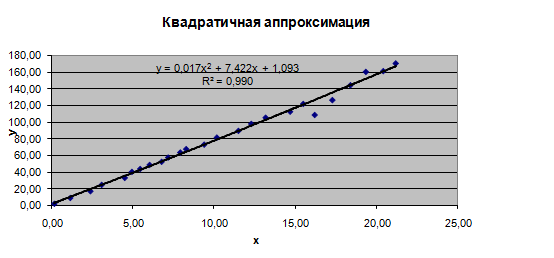
Рисунок 9
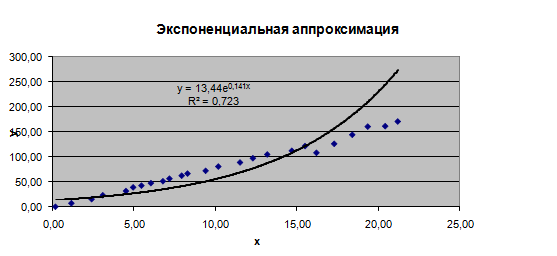
Рисунок 10
Как видно из рисунков 8-10, результаты операций, выполненных «вручную» соответствую результатам, полученным с помощью встроенных в мастер диаграмм функций. Здесь также самым лучшим способом аппроксимации является квадратичная, коэффициент детерминированности которой равен 0,990 и менее всех остальных отличен от 1.
Функция ЛИНЕЙН
Результаты, полученные с помощью функции ЛИНЕЙН совпадают как с результатами линейной аппроксимации, выполненной «вручную», так и с результатами, полученными при построении графика мастером диаграмм программы Microsoft Excel.
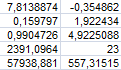
Рисунок 11
Вывод
Выполнение аппроксимации в табличном процессоре Microsoft Excel способами показывают один и тот же результат – наиболее точной является полиномиальная (в данном случае – квадратичная) аппроксимация. Вывод об этом сделан мною из сравнения коэффициентов детерминированности.
Выполнение аппроксимации в программе MathCAD
Введение
Аппроксимация данных с учетом их статистических параметров относится к задачам регрессии. Они обычно возникают при обработке экспериментальных данных, полученных в результате измерений процессов или физических явлений, статистических по своей природе (как, например, измерения в радиометрии и ядерной геофизике), или на высоком уровне помех (шумов). Задачей регрессионного анализа является подбор математических формул, наилучшим образом описывающих экспериментальные данные.
1. Линейная регрессия
Линейная регрессия в системе MathCAD выполняется по векторам аргумента Х и отсчетов Y функциями:
intercept(X,Y) – вычисляет параметр а1, смещение линии регрессии по вертикали;
slope(X,Y) – вычисляет параметр a2, угловой коэффициент линии регрессии.
Полученные значения коэффициентов используем в уравнении регрессии y(x) = = a1+a2*x.
Функция corr(Y,y(x)) вычисляет коэффициент корреляции Пирсона. Чем он ближе к 1, тем точнее обрабатываемые данные соответствуют линейной зависимости.
2. Полиномиальная регрессия
Одномерная полиномиальная регрессия с произвольной степенью n полинома и с произвольными координатами отсчетов в MathCAD выполняется функциями:
regress(X,Y,n) – вычисляет вектор S, в составе которого находятся коэффициенты ai полинома n-й степени;
Значения коэффициентов ai могут быть извлечены из вектора S функцией submatrix(S, 3, length(S)-1, 0, 0).
Полученные значения коэффициентов используем в уравнении регрессии y(x) = = a1+a2*x+a3*x2
3. Нелинейная регрессия
Для простых типовых формул аппроксимации предусмотрен ряд функций нелинейной регрессии, в которых параметры функций подбираются программой MathCAD. К их числу относится функция expfit(X,Y,S), которая возвращает вектор, содержащий коэффициенты a1, a2 и a3 экспоненциальной функции y(x) = a1·exp(a2·x) + a3. В вектор S вводятся начальные значения коэффициентов a1, a2 и a3 первого приближения.
Линейная аппроксимация в программе MathCAD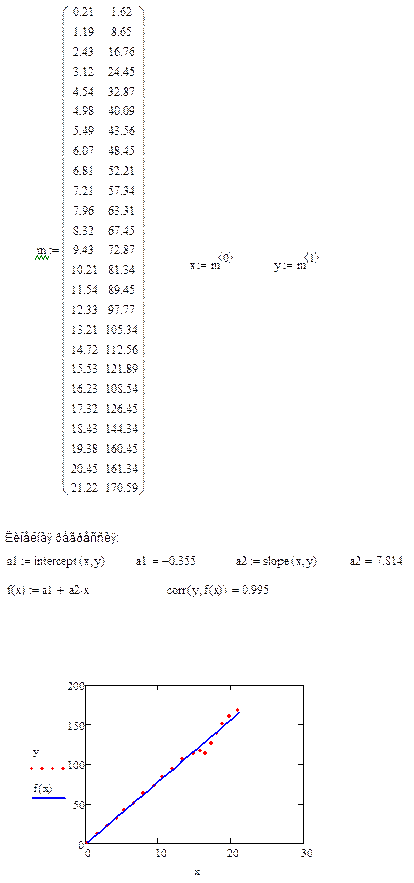 
Рисунок 12
Экспоненциальная аппроксимация в программе MathCAD
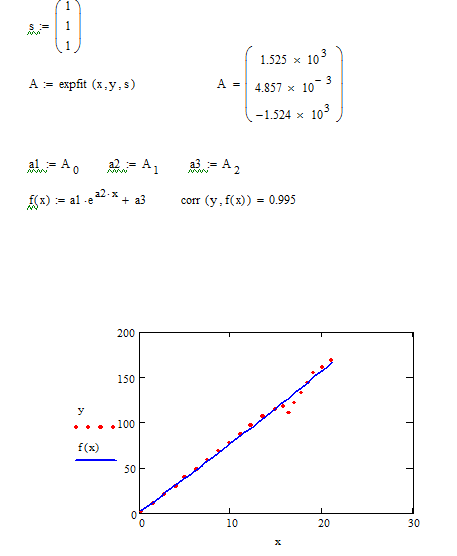
Рисунок 13
Полиномальная (квадратичная аппроксимация в программе MathCAD
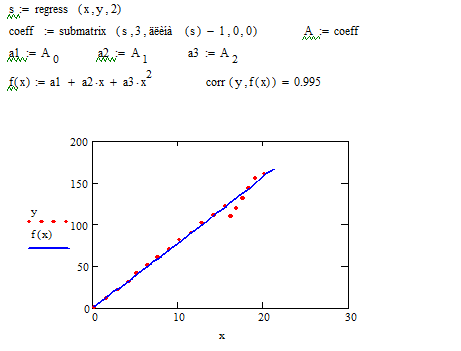
Рисунок 14
Вывод
Результаты аппроксимации, выполненной в программе MathCAD полностью совпали с результатами, полученными в Excel, что подтвердило правильность произведенных вычислений. Наилучшим способом аппроксимации оказался полиномиальный – его коэффициент детерминированности весьма высок и составляет приблизительно 0,995. Для сравнения привожу таблицу:
| Excel (ручной метод) | Excel (Мастер Диаграмм) | Excel (ЛИНЕЙН) | MathCAD | |
| Линейная | 0,99047263 | 0,990 | 0,0990 | 0,995 |
| Полиномальная | 0,99063894 | 0,990 | – | 0,995 |
| Экспоненциальная | 0,52482597 | 0,723 | – | 0,995 |
Таблица 3
Список литературы
1. Ахметов К.С. Windows 95 для всех. - М.:ТОО "КомпьютерПресс", 1995.
2. Вычислительная техника и программирование. Под ред. А.В. Петрова. М.: Высшая школа, 1991.
3. Гончаров A., Excel 97 в примерах. — СПб: Питер, 1997.
4. Левин А., Самоучитель работы на компьютере. - М.: Международное агентство А.Д.Т., 1996.
5. Информатика: Методические указания к курсовой работе. Санкт-Петербургский горный институт. Сост. Д.Е. Гусев, Г.Н. Журов. СПб, 1999
