Большинство используемых в радиотехнике сигналов являются случайными. Случайность сигналов обусловлена: во-первых принципиальной невозможностью передачи информации с помощью заранее известных (детерминированных) сигналов, во-вторых наличием различного рода помех – шумы в электронных приборах и радиоэлементах, изменения свойств среды распространения радиоволн, искусственно создаваемые помехи и т.п.
В связи со случайным характером используемых сигналов для их характеристики используют математический аппарат теории вероятностей, математической статистики и теории случайных процессов.
В основе теории вероятностей лежит ряд понятий и аксиом, которые используются в теории случайных сигналов. Перечислим некоторые из эти положений. Существует понятие полного множества случайных событий или элементарных исходов W={А1,А2,…Аi…An}. Символы Аi отображают все возможные исходы некоторого случайного эксперимента. Каждому событию АiÎW сопоставляется вещественное число Р(Аi), которое называется вероятностью этого события. В отношении вероятностей справедливы следующие аксиомы:
1. Вероятность всегда положительна и меньше 1, т.е. 0£Р(Аi)£1.
2. Сумма вероятностей полного множества событий есть событие достоверное и для него справедливо
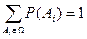
3. Если А сложное событие, в которое входит несколько простых событий Аi то его вероятность равна сумме всех элементарных вероятностей

Практически, общепринято оценивать вероятность события относительной частотой благоприятных исходов. Если проведено N независимых испытаний, причем в n из них наблюдалось событие А, то эмпирическая (выборочная) оценка вероятности Р(А), которую можно получить из этой серии опытов, равна

В радиотехнике чаще приходится иметь дело со случайными процессами. Допустим, в результате наблюдения (приема, испытания) стала известна некоторая случайная функция х1(t) сигнала (рисунок 20.1). Такую случайную функцию называют реализацией случайного процесса. Теоретически случайный процесс можно полностью охарактеризовать только с помощью бесконечной совокупности реализаций
 |
Рисунок 20.1
| x1(t), x2(t), …xk(t)… x¥(t) | (20.1) |
Совокупность реализаций (20.1) случайного сигнала принято называть статистическим ансамблем. Полный ансамбль реализаций в совокупности (20.1) образует случайный процесс X(t). В момент t=t1 каждая из реализаций xk(t) принимает некоторое значение. В качестве одной из характеристик случайного сигнала используют вероятность события, состоящего в том, что случайное значение сигнала в k-й реализации попадает в некоторый интервал значений (a, b на рисунке 20.1в). Эта вероятность определяется выражением

| (20.2) |
Функцию p(x,t1), представляющую дифференциальный закон распределения случайной величины (СВ) называют одномерной плотностью вероятности, а Рt – интегральной функцией распределения. Для дискретных случайных величин аналогичная функция распределения может быть записана в форме:

| (20.3) |
где дискретная случайная величина xi принимает значение с вероятностями: (Р1, Р2…Рi…Рm…).
Для случайного непрерывного сигнала, принимающего любые значения в некоторой ограниченной области (xmin, xmax) справедливо равенство
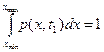 , ,
|
которое называют условием нормировки, оно аналогично аксиоме 2.




