Расчет продольных ребер по раскрытию трещин.

Расчет трещиностойкости продольных ребер.

Расчет продольных ребер по образованию трещин.

 

Расчет железобетонных элементов по трещинообразованию выполняют на действие нормативных нагрузок.

(3.7.1)

где и временная и постоянная нормативные нагрузки на 1м² (см. Таблицу сбор нагрузок);

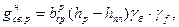(3.7.2)

где - высота продольного ребра;

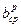- средняя ширина ребра ;

- объемный вес тяжелого бетона ;

- коэффициент надежности по нагрузке.

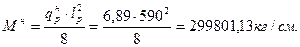(3.7.3)

Расчет железобетонных элементов по образованию нормальных трещин производится из условия:

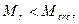
Условие не выполняется, трещины образуются.

где: М_r ¾ момент внешних сил;

М_crc — момент, воспринимаемый сечением, определяемый по формуле:

, (3.7.4)

где: - расчетное сопротивление бетона осевому растяжению (по второй группе предельных состояний);

W_pl ¾ упруго пластический момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона;

(3.7.5)

где W_red ¾ момент сопротивления для растянутой грани приведенного сечения, определяемый по правилам сопротивления упругих материалов.

g - коэффициент для прямоугольных сечений принимается равным 1,75.

(3.7.6)

где 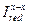- приведенный момент инерции относительно оси х-х, проходящей через центр тяжести сечения;

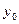- расстояние от максимально удаленной грани сечения до центра тяжести сечения.

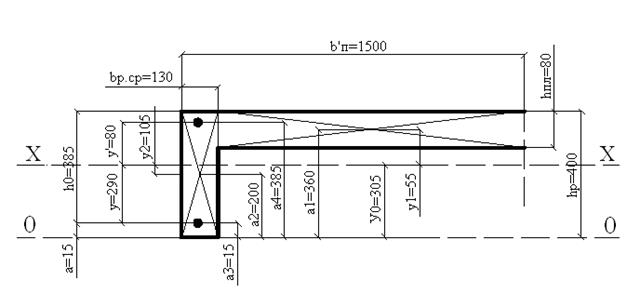
Рис. 10

 

Положение оси х-х определяется по формуле:

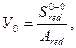(3.7.7)

 

где - площадь приведенного сечения:

(3.7.8)

где - площадь полки приведенного сечения; 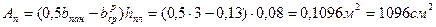(3.7.9)

- площадь ребра приведенного сечения;

(3.7.10)

- площадь рабочей арматуры;

- площадь конструктивной арматуры;

- коэффициент привидения бетона к арматуре

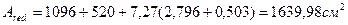
(3.7.11)

где - расстояния от нижней грани сечения (оси 0-0) до центра тяжести приведенных сечений;

; (3.7.12)

(3.7.13)

(3.7.14)

 

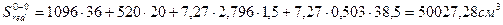
(3.7.15)

где: 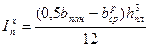- момент инерции полки; (3.7.16)

- момент инерции ребра; (3.7.17)

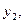
- расстояния от центров тяжести приведенных сечений до оси х-х проходящей через центр тяжести всего сечения;

(3.7.18)

(3.7.19)

(3.7.20)

(3.7.21)

Напряжения, возникающие в растянутой зоне:

(3.7.22)

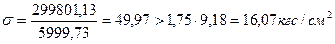- условие прочности не выполняется, поэтому необходимо выполнить расчет ребра по раскрытию трещин.

Расчет продольных ребер по раскрытию трещин.

 

Сущность расчета по раскрытию трещин нормальных и наклонных к продольной оси, заключается в определении ширины раскрытия трещин на уровне растянутой арматуры (а_crc) и сравнивают ее с предельной шириной раскрытия [а_lim].

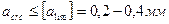
Если это условие выполняется, то конструкция удовлетворяет требованиям по ширине раскрытия трещины.

Ширину раскрытия трещин, нормальных к продольной оси элемента, a_crc, мм, следует определять по формуле:

(3.7.23)

где:

d ¾ коэффициент, принимаемый равным 1 для изгибаемых элементов;

h - коэффициент, принимаемый равным:

при стержневой арматуре периодического профиля 1,0

при стержневой арматуре гладкой 1,3

при проволочной арматуре периодического профиля и канатах 1,2

при гладкой арматуре 1,4

 

j_l — коэффициент, принимаемый равным для продолжительного действия постоянных и

длительных нагрузок для конструкций из тяжелого бетона естественной влажности;

,

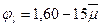где ¾ коэффициент армирования сечения, принимаемый равным отношению площади сечения арматуры S к площади сечения бетона (при рабочей высоте h_o и без учета сжатых свесов полок), но не более 0,02.

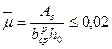(3.7.24)

 

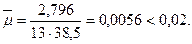
(3.7.25)

 

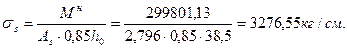(3.7.26)

 

d — диаметр растянутой арматуры, мм.

 

Условие выполняется.

4. РАСЧЁТ УСИЛИЙ В ЭЛЕМЕНТАХ ПОПЕРЕЧНОЙ РАМЫ КАРКАСА.

 

На поперечную раму каркасного здания действуют ветровая, снеговая, крановая и постоянная нагрузки. Сбор нагрузок и расчет внутренних усилий от их действия произведен с помощью программного комплекса SCAD в курсовом проекте “Металлические каркасные здания”.

По результатам расчета построены огибающие эпюр для расчета колонны по ряду А на I-е сочетания нагрузок наиневыгаднейшей комбинации загружения внутри сочетания.

 

 

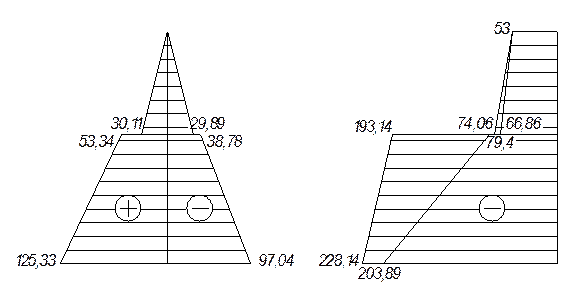
Рис. 11. Огибающие эпюры моментов

 

АРМИРОВАНИЕ КОЛОННЫ