Ecли ||A||I=… норма матрицы по столбцам <=1, но хотя бы для одного i выполняется строгое неравенство 
, то метод Зейделя сходится.
Call zeidel(eps, x, n)
For i = 1 To 4
x(i) = 0: Next i: n = 0
Do: n = n + 1: l = False
For i = 1 To 4: x0(i) = x(i): Next i
For i = 1 To 4: x(i) = b(i) / a(i, i)
For j = 1 To i – 1: x(i) = x(i) - a(i, j) / a(i, i) * x0(j): Next j
For j = i + 1 To 4: x(i) = x(i) - a(i, j) / a(i, i) * x(j): Next j
If Abs(x(i) - x0(i)) > e Then: l = True: End If: Next i
Loop Until Not l: End Sub
Численное интегрирование. Метод прямоугольников с недостатком.
Встречаются модификации метода прямоугольников:
-метод левых прямоугольников
-метод правых прямоугольников
-метод средних прямоугольников
Абсолютная погрешность формулы прямоугольников на отрезке от a до b равна сумме погрешностей на каждом элементарном интервале.
Абсолютная погрешность:
xn = PrN(a, b, eps, n)
k = 1: s1 = 0: n = 0
Do
s = s1: k = k * 2: n = n + 1
dx = (b - a) / k
s1 = 0
For x = a To b - dx + e Step dx
s1 = s1 + f(x)
Next x
s1 = dx * s1
Loop Until Abs(s - s1) <= e
PrN = s1
End Function
Численное интегрирование. Метод прямоугольников с избытком.
Метод прямоугольников (левые, правые)
Встречаются модификации метода прямоугольников:
-метод левых прямоугольников
-метод правых прямоугольников
Абсолютная погрешность формулы прямоугольников на отрезке от a до b равна сумме погрешностей на каждом элементарном интервале.
Абсолютная погрешность:
xm = PrM(a, b, eps, n)
k = 1: s1 = -1: n = 0
Do
s = s1: k = k * 2: n = n + 1
dx = (b - a) / k
s1 = 0
For x = a + dx To b + e Step dx
s1 = s1 + f(x)
Next x
s1 = dx * s1
Loop Until Abs(s - s1) <= e
PrM = s1
End Function
Численное интегрирование. Метод трапеций.
Формула метода трапеции:
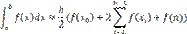
xt = Trap(a, b, eps, n)
Dim k As Currency
Dim s, s1, x, dx As Double
k = 1: s1 = -1: n = 0
Do
s = s1: k = k * 2: n = n + 1
dx = (b - a) / k
s1 = (f(a) + f(b)) / 2
For x = a + dx To b - dx + e Step dx
s1 = s1 + f(x): Next x
s1 = dx * s1
Loop Until Abs(s - s1) <= e
Trap = s1: End Function
Поиск минимума функции вида f(x). Метод деления отрезка пополам.
Function Dix(a, b, e, n) As Double
Dim x1, x2 As Double
n = 0
While (b - a) > e
n = n + 1
x1 = a + 0.25 * (b - a)
x2 = a + 0.75 * (b - a)
If f(x1) < f(x2) Then
b = x2
Else
a = x1
End If
Wend
Dix = (a + b) / 2
End Function
28. Поиск минимума функции вида f(x). Метод «Золотого сечения».
Алгоритм метода:
1) Вычисляется значение f(x1), где x1=a+0,382(b-a)
2) Вычисляется f(x2), x2=b-0,382(b-a)
3) Определяется новый интервал: (a;x2) – 1ый случай или (x1;b) – 2ой случай, в котором локализован минимум.
4) Внутри получившегося интервала находится новая точка в 1ом случае x1, во 2ом случае x2, стоящие от его конца на расстоянии, составляющем 0,382 от его длины. В этой точке рассчитывается значение f(x), затем вычисления повторяются с пункта 3 до тех пор, пока величина интервала неопределенности станет 
.
Function Gold(a, b, e, n) As Double
Dim x1, x2 As Double: n = 0
While (b - a) > e: n = n + 1
x1 = a + 0.318 * (b - a)
x2 = a + 0.682 * (b - a)
If f(x1) < f(x2) Then: b = x2: Else: a = x1: End If
Wend: Gold = (a + b) / 2: End Function
