Арифметической прогрессией называется числовая последовательность, задаваемая двумя параметрами 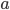 , ,  и законом и законом  , ,    — разность данной арифметической прогрессии; — разность данной арифметической прогрессии;
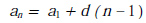 Формула разности арифметической прогрессии:
Формула разности арифметической прогрессии:
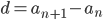 Формула суммы n-первых членов арифметической прогрессии
Формула суммы n-первых членов арифметической прогрессии
 
| Геометрической прогрессией называется числовая последовательность задаваемая двумя параметрами b, q (q ≠ 0) и законом  , ,  , ,  Число
Число  - знаменатель данной геометрической прогрессии. - знаменатель данной геометрической прогрессии.
 Формула знаменателя геометрической прогрессии:
Формула знаменателя геометрической прогрессии:
 Формула суммы n-первых членовгеометрической прогрессии
Формула суммы n-первых членовгеометрической прогрессии
  где, q ≠ 1 где, q ≠ 1
|
| Тип 1. Выписано несколько последовательных членов арифметической прогрессии: …; −9; x; −13; −15; … Найдите член прогрессии, обозначенный буквой x. Решение. Найдем разность арифметической прогрессии: d = - 15 – (- 13) = - 2. Поэтому x = - 9 + (- 2) = - 11. Ответ: - 11 | Тип 2.
Задана арифметическая прогрессия, где пятый и десятый члены равны соответственно 38 и 23. Найти пятнадцатый член прогрессии и сумму ее десяти первых членов.
Решение:

| Тип 3.
Выписано несколько последовательных членов геометрической прогрессии: …; 150; x; 6; 1,2; … Найдите член прогрессии, обозначенный буквой x.
Решение.
Найдем знаменатель геометрической прогрессии: d =  = =  . Поэтому, x = 150 . Поэтому, x = 150  = 30
Ответ: 30. = 30
Ответ: 30.
| Тип 4.
Задана геометрическая прогрессия 2,6,18,... Найти десятый член прогрессии и сумму её двенадцати первых членов.
Решение:



|
Задание 7.
Алгебраические выражения (целые и рациональные).
Формулы сокращенного умножения

| Разложение на множители 1. Вынесение общего множителя за скобки 2. Применение формул сокращенного умножения 3. Способ группировки 4. Разложение квадратного трехчлена на множители ax2 + bx + c = а (х – х1) (х – х2) | Приведение к общему знаменателю 1. Деление 2. НОК 3. Крест на крест |
Тип 1.
Найдите значение выражения  при при  .
Решение. Подставим в выражение числовое значение переменной: .
Решение. Подставим в выражение числовое значение переменной:
 Ответ:
Ответ: 
| Тип 2

| Тип 3

| |
Тип 4

| Тип 5 | Тип 6 |
Задание 8.
Неравенства и их системы

| 
| ||
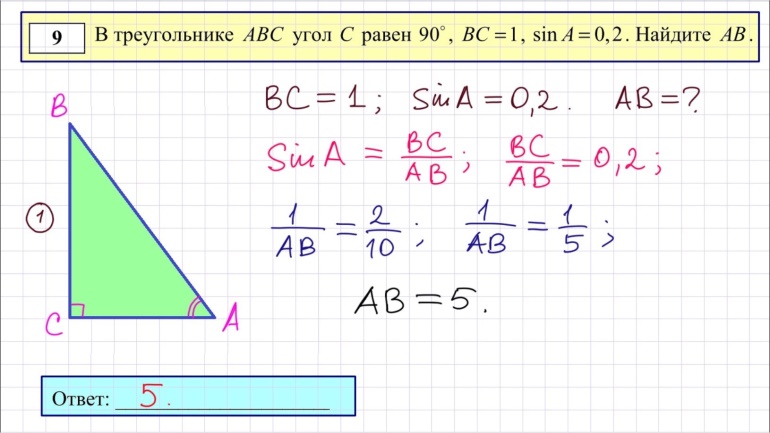
Задание 9
Треугольники, четырёхугольники, многоугольники и их элементы

| 
| 
|

|

|
Задание 10
Окружность, круг и их элементы


|

| 
|

| 
| 
|
Задание 11
Площади фигур
Тип 1
 Тип 2
Тип 2
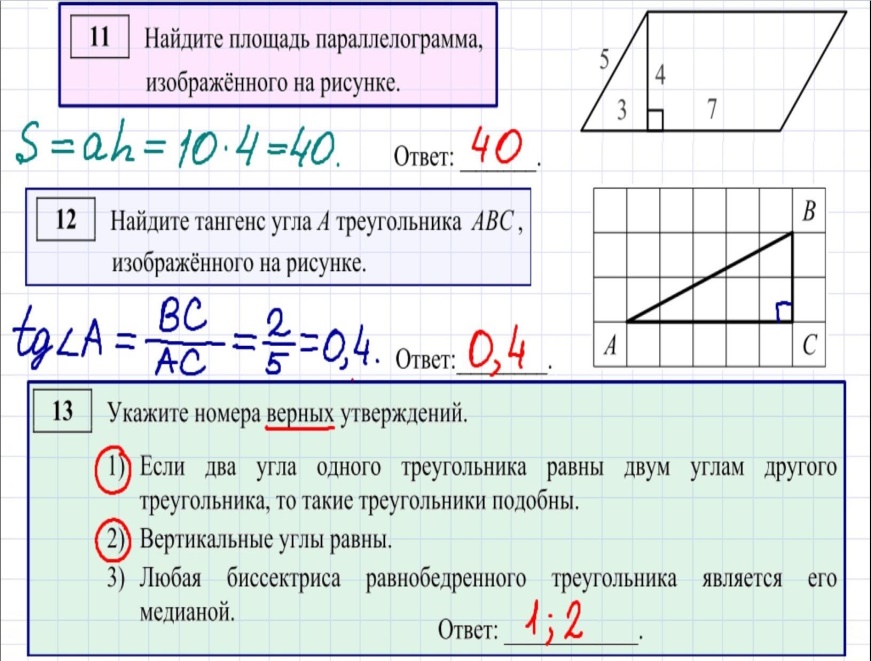
| 
| Тип 4

|
Тип 3

| ||
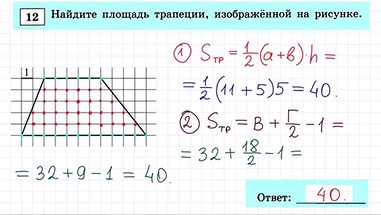
Задание 12
Фигуры на квадратной решётке


| ||

| 
|
Задание 14
Анализ таблиц

| 
|

|
Задание 15
Анализ графиков
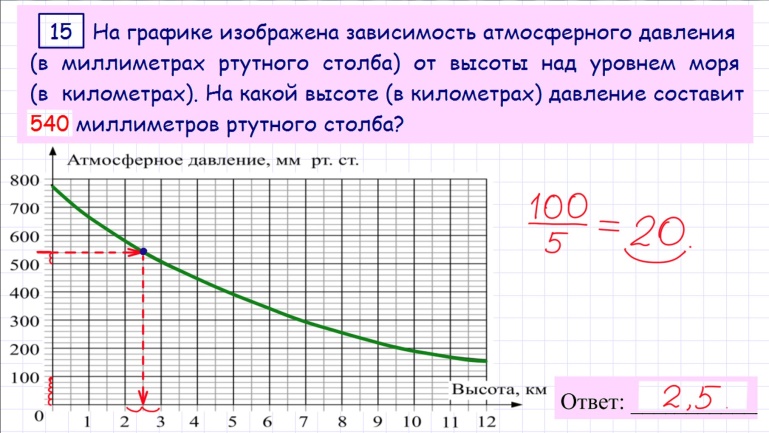
| 
| |
Задание 16





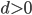 — арифметическую прогрессию называют возрастающей;
— арифметическую прогрессию называют возрастающей; — арифметическую прогрессию называютубывающей;
— арифметическую прогрессию называютубывающей;
