Математическая статистика и прогнозирование
Контрольная работа №1
Методические указания к решению задач
Определение закона распределения случайной величины по статистическим данным
1.1. В разнообразных видах практической деятельности встречается такая задача. Наблюдается некоторая случайная величина  , закон распределения которой не известен. Требуется определить этот закон из опыта или проверить гипотезу о том, что эта случайная величина подчинена определенному закону распределения.
, закон распределения которой не известен. Требуется определить этот закон из опыта или проверить гипотезу о том, что эта случайная величина подчинена определенному закону распределения.
В результате наблюдений (эксперимента, исследований) имеем ряд значений случайной величины:
| … | n | |||

| 
| 
| 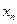
|
Такой ряд называется первичным (простым) рядом наблюдений или выборкой значений случайной величины, при этом число наблюденных значений  называется объемом (размером) выборки.
называется объемом (размером) выборки.
Для заданной выборки может быть построена статистическая (эмпирическая) функция распределения случайной величины Х -  . Значение функции
. Значение функции  для каждого действительного числа
для каждого действительного числа 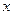 полагается равным частоте события
полагается равным частоте события  в данной выборке:
в данной выборке:
 , (2)
, (2)
где  - число наблюдений в выборке, меньших
- число наблюдений в выборке, меньших  .
.
1.2. Чтобы описать свойства статистической функции распределения расположим наблюдения в порядке возрастания значений:

Такой ряд называется вариационным рядом.
Основные свойства  следующие:
следующие:
1) Функция  не убывает:
не убывает:
 , для
, для 
2) Если  , то слева от любого
, то слева от любого 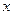 из промежутка
из промежутка 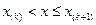 лежит одно и то же число наблюдений (именно
лежит одно и то же число наблюдений (именно  ). Поэтому функция
). Поэтому функция  сохраняет постоянное значение
сохраняет постоянное значение  во всех точках этого промежутка, включая точку
во всех точках этого промежутка, включая точку 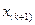 :
:
 , для
, для 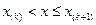 .
.
В самой же точке 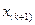 функция
функция  совершает скачок на величину
совершает скачок на величину  , где
, где  - число наблюдений в ряду, в точности равных
- число наблюдений в ряду, в точности равных 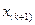 .
.
3) Слева от наименьшего наблюденного значения, включая и само это значение, функция  равна 0:
равна 0:
 , для
, для 
4) Справа от наибольшего наблюденного значения функция  равна 1:
равна 1:
 , для
, для 
Но самые важные свойства  следующие:
следующие:
5) Согласно закону больших чисел (теореме Бернулли) при каждом 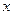
 сходится к
сходится к  по вероятности:
по вероятности:
Для каждого 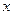 и каждого
и каждого 

6) Более того, с вероятностью единица имеет место равномерная по  сходимость
сходимость  к
к  при
при  (теорема Гливенко):
(теорема Гливенко):
 с вероятностью 1,
с вероятностью 1,
где значок  означает точную верхнюю грань (максимальное значение) модуля разности между
означает точную верхнюю грань (максимальное значение) модуля разности между  и
и  , а оговорка «с вероятностью 1» означает, что для любой наблюденной последовательности значений случайной величины указанный предел будет равен 0.
, а оговорка «с вероятностью 1» означает, что для любой наблюденной последовательности значений случайной величины указанный предел будет равен 0.
Благодаря свойствам 5 и 6 построение эмпирической функции распределения решает в принципе задачу определения закона распределения случайной величины.
1.3. Рассмотрим построение функции  на примере.
на примере.
Задача 1.
10 раз повторяли серию из 100 подбрасываний монеты и подсчитывали число выпадений герба в каждой серии. Получили следующую выборку:
Требуется построить статистическую функцию распределения.
Решение.
Построим вариационный ряд наблюдений:
Составим таблицу (1):
В первый столбец последовательно выпишем различные значения вариационного ряда  ;
;
Во втором столбце для каждого значения укажем число повторений этого значения в выборке, так называемую абсолютную частоту 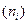 ;
;
В третьем столбце вычислим относительные частоты наблюдений, т.е. результат деления абсолютных частот на общее число наблюдений  ;
;
В четвертом столбце относительные частоты представим нарастающим итогом, причем для первого значения укажем ноль. Это и есть значения статистической функции распределения в каждой точке скачка  .
.
Таблица (1) позволяет выписать формулы (1), определяющие статистическую функцию распределения  .
.
Таблица 1

| 
| 
| 
|
| 0,1 | |||
| 0,1 | 0,1 | ||
| 0,2 | 0,2 | ||
| 0,1 | 0,4 | ||
| 0,1 | 0,5 | ||
| 0,3 | 0,6 | ||
| 0,1 | 0,9 | ||
 (1)
(1)
График функции  приведен на Рис.1. Он имеет вид ступенчатой возрастающей функции, причем в каждой точке скачка функция непрерывна слева: на рисунке 1 значение 0,2 в точке 46 выделено жирной точкой, предел справа в это точке равен 0,4.
приведен на Рис.1. Он имеет вид ступенчатой возрастающей функции, причем в каждой точке скачка функция непрерывна слева: на рисунке 1 значение 0,2 в точке 46 выделено жирной точкой, предел справа в это точке равен 0,4.

Рисунок 1
1.4 Статистическая функция распределения имеет ступенчатый характер как для дискретной, так и для непрерывной случайной величины.
Для дискретной случайной количество скачков будет сохраняться или медленно возрастать при увеличении числа наблюдений, а величины этих скачков будут стремиться к истинным вероятностям соответствующих значений.
Так в рассмотренном примере выборка размером 10 имела 9 скачков. Были смоделированы выборки объемом 50 и 100 наблюдений из данного распределения вероятностей. Для 50 получили 16 скачков, для 100 – 19 скачков. Но вообще-то в рассмотренном примере количество скачков может достигнуть 100.
Если количество различных значений дискретной случайной величины невелико, то построение функции  можно выполнять описанным выше способом. На самом деле для дискретной случайной величины нужны статистические частоты наблюденных значений, т.е. статистический ряд распределения.
можно выполнять описанным выше способом. На самом деле для дискретной случайной величины нужны статистические частоты наблюденных значений, т.е. статистический ряд распределения.
Для непрерывной случайной величины количество скачков будет мало отличаться от  , поэтому построение
, поэтому построение  описанным способом в этом случае возможно лишь при небольшом объеме выборки. При больших
описанным способом в этом случае возможно лишь при небольшом объеме выборки. При больших  построение
построение  описанным способом становится чрезвычайно трудоемким, да и сама функция, содержащая сотни скачков, оказывается недостаточно наглядной. Эти проблемы устраняются путем преобразования первичного ряда наблюдений в так называемый группированный статистический ряд.
описанным способом становится чрезвычайно трудоемким, да и сама функция, содержащая сотни скачков, оказывается недостаточно наглядной. Эти проблемы устраняются путем преобразования первичного ряда наблюдений в так называемый группированный статистический ряд.
1.5. Группированный статистический ряд можно построить следующим способом.
Первичная выборка преобразуется в вариационный ряд. Далее определяется размах выборки:

Определяется количество разрядов, интервалов, на которые будут разделены наблюденные значения. Количество таких интервалов, как правило, от 10 до 20. При этом желательно, чтобы эти интервалы были равной длины. Но иногда отдельные интервалы приходится объединять, если они содержат слишком мало значений. При высокой же частоте изменения значений  в некоторых областях исходные интервалы приходится разбивать на более мелкие интервалы.
в некоторых областях исходные интервалы приходится разбивать на более мелкие интервалы.
Будем считать, что область значений случайной величины разбивается на  разрядов длины
разрядов длины 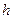 :
:
 .
.
При вычислении 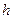 удобно округлить до одного-двух знаков после запятой в большую сторону, чтобы наблюдение
удобно округлить до одного-двух знаков после запятой в большую сторону, чтобы наблюдение  попало внутрь последнего разряда. Границы
попало внутрь последнего разряда. Границы  - го разряда будем обозначать через
- го разряда будем обозначать через 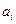 и
и  . Так что вся область изменения случайной величины разлагается в сумму
. Так что вся область изменения случайной величины разлагается в сумму  непересекающихся разрядов:
непересекающихся разрядов:
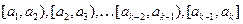
Далее подсчитываем количество наблюдений, попавших в  -ый разрядов, так называемые абсолютные частоты -
-ый разрядов, так называемые абсолютные частоты -  , относительные частоты
, относительные частоты  и накопленные частоты:
и накопленные частоты:  . При построении графика
. При построении графика  полученные значения
полученные значения  соединяют отрезками прямой или плавной линией, что вполне оправдано, так как предельная функция
соединяют отрезками прямой или плавной линией, что вполне оправдано, так как предельная функция  является непрерывной.
является непрерывной.
1.5 Выполним описанный расчет на данных конкретной задачи.
Задача 2.
Дана выборка размера 100 из нормальной совокупности с математическим ожиданием 0 и дисперсией 1. Данные размещены по столбцам в таблице (2). Построить статистическую функцию распределения и сравнить ее с функцией стандартного нормального распределения.
Таблица 2
| № п/п | ||||||||||
| -0,1116 | -2,0578 | -0,6008 | 1,5535 | -0,1615 | -2,4063 | 0,5496 | -0,4507 | -2,2961 | 1,5484 | |
| -0,7394 | -0,2984 | 1,3807 | -1,0874 | -0,4740 | 0,3993 | 0,6486 | -0,1383 | -0,7128 | -0,8536 | |
| 0,6354 | 0,6409 | -0,6593 | -0,6599 | -0,9447 | 1,2911 | -0,7125 | -0,8667 | -0,2884 | -1,3493 | |
| -1,0073 | 0,7695 | 1,1176 | 1,2506 | -0,2533 | -0,5885 | 2,7876 | 0,6535 | -1,2660 | 0,9677 | |
| -0,6055 | -0,0093 | -0,3430 | -1,0980 | 1,8154 | -0,6324 | -0,3313 | 1,1891 | -2,2253 | 0,2445 | |
| 0,5294 | 0,9830 | 0,4903 | -1,6584 | -1,0040 | -1,4356 | 0,2834 | -1,4466 | 1,9075 | -1,7894 | |
| 1,2392 | 0,9453 | -0,5459 | 0,0924 | 0,0470 | -0,0108 | -0,3276 | -0,7358 | 1,4536 | 1,0812 | |
| 1,8320 | 1,0247 | -0,7933 | -0,0492 | -0,4918 | 0,4732 | -0,1317 | -0,2844 | -0,3376 | -0,1067 | |
| -1,5434 | -0,7626 | -0,2553 | 0,4369 | 0,6216 | -0,7125 | -0,7496 | -1,4501 | -0,7563 | -0,0888 | |
| 0,1474 | -1,4730 | -1,8222 | 0,8957 | -0,5583 | -0,3553 | -1,0774 | 1,4407 | -0,4736 | 0,1044 |
Решение.
Вычисления удобно выполнять в Excel. Там сгенерированные исходные данные располагаются в одном столбце. Их легко отсортировать по возрастанию и найти минимальное и максимальное значение, размах и длину разряда при числе разрядов, равном 10:
| xmin | -2,4063 |
| xmax | 2,7876 |
| R | 5,1939 |
| k | |
| h | 0,52 |
Теперь заполняем таблицу (3) группированного статистического ряда
Таблица 3

| 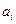
| 
| 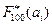
| 
| 
|
| -2,4063 | 0,00 | 0,008057 | 0,008057 | ||
| -1,8863 | 0,04 | 0,029625 | 0,010375 | ||
| -1,3663 | 0,12 | 0,085916 | 0,034084 | ||
| -0,8463 | 0,22 | 0,198681 | 0,021319 | ||
| -0,3263 | 0,48 | 0,372083 | 0,107917 | ||
| 0,1937 | 0,66 | 0,576779 | 0,083221 | ||
| 0,7137 | 0,79 | 0,762281 | 0,027719 | ||
| 1,2337 | 0,88 | 0,891335 | 0,011335 | ||
| 1,7537 | 0,96 | 0,960256 | 0,000256 | ||
| 2,2737 | 0,99 | 0,988507 | 0,001493 | ||
| 2,7937 | 1,00 | 0,997394 | 0,002606 | ||
| D | 0,107917 |
Здесь использованы следующие обозначения:
 - номер разряда и его левой границы;
- номер разряда и его левой границы;
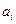 - значение левой границы разряда;
- значение левой границы разряда;
 - число наблюдений, удовлетворяющих неравенству
- число наблюдений, удовлетворяющих неравенству  ;
;
 - функция стандартного нормального распределения;
- функция стандартного нормального распределения;
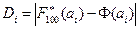 ;
;
 .
.
Подсчет чисел  выполнен с помощью функции Excel СЧЁТЕСЛИ (диапазон; условие). При большом
выполнен с помощью функции Excel СЧЁТЕСЛИ (диапазон; условие). При большом  такой подсчет затруднительно сделать без компьютера.
такой подсчет затруднительно сделать без компьютера.
На рисунке 2 показаны функции  и
и  для сравнения. Видно достаточно хорошее соответствие. Более точное заключение сделаем несколько позже, когда будем рассматривать критерии согласия.
для сравнения. Видно достаточно хорошее соответствие. Более точное заключение сделаем несколько позже, когда будем рассматривать критерии согласия.
1.6. На практике часто группированный статистический ряд представляют в виде графика гистограммы.
Чтобы построить гистограмму, нужно по оси абсцисс отложить границы разрядов, и на каждом разряде как на основании построить прямоугольник с площадью, равной частоте разряда.
Для этого нужно частоту разряда разделить на длину разряда и полученное число взять в качестве высоты прямоугольника. Для  -го разряда получаем формулу:
-го разряда получаем формулу:
 ,
,
где  - высота прямоугольника, а
- высота прямоугольника, а  - относительная частота
- относительная частота  -го разряда.
-го разряда.

Рисунок 2
Обозначим через 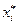 абсциссу середины
абсциссу середины  -го разряда. Тогда точка
-го разряда. Тогда точка 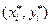 есть середина верхнего основания прямоугольника
есть середина верхнего основания прямоугольника  -го разряда. Соединяя эти точки отрезками прямых линий, получим полигон частот, который позволяет сравнить гистограмму с функцией плотности теоретического распределения, к которой стремится гистограмма при увеличении
-го разряда. Соединяя эти точки отрезками прямых линий, получим полигон частот, который позволяет сравнить гистограмму с функцией плотности теоретического распределения, к которой стремится гистограмма при увеличении  и неограниченном уменьшении длины разряда.
и неограниченном уменьшении длины разряда.
Задача 3.
Используя данные задачи 2 построить на одном графике для сравнения гистограмму, полигон частот и функцию плотности стандартного нормального распределения.
Решение.
Используя таблицу (3) составим таблицу (4) для построения требуемых графиков.
Графики представлены на рисунке 3.
Графики показывают небольшую левую асимметрию и выброс в центре, обусловленные случайными отклонениями.
Таблица 4

| 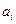
| 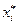
| 
| 
| 
| 
|
| -3,0000 | 0,00 | 0,0000 | 0,004432 | |||
| -2,4063 | -2,1463 | 0,04 | 0,0769 | 0,022056 | ||
| -1,8863 | -1,6263 | 0,08 | 0,1538 | 0,067335 | ||
| -1,3663 | -1,1063 | 0,10 | 0,1923 | 0,156863 | ||
| -0,8463 | -0,5863 | 0,26 | 0,5000 | 0,278849 | ||
| -0,3263 | -0,0663 | 0,18 | 0,3462 | 0,378255 | ||
| 0,1937 | 0,4537 | 0,13 | 0,2500 | 0,391531 | ||
| 0,7137 | 0,9737 | 0,09 | 0,1731 | 0,309254 | ||
| 1,2337 | 1,4937 | 0,08 | 0,1538 | 0,186393 | ||
| 1,7537 | 2,0137 | 0,03 | 0,0577 | 0,085726 | ||
| 2,2737 | 2,5337 | 0,01 | 0,0192 | 0,030086 | ||
| 2,7937 | 0,008057 | |||||
| 3,0000 | 0,004432 |

Рисунок 3
- Критерии согласия эмпирического и теоретического законов распределения.
Построенные на рисунках 2 и 3 графики позволяют высказать предположение о том, что наблюдаемая случайная величина имеет нормальное распределение с математическим ожиданием 0 и дисперсией 1 -  . Способы, позволяющие проверить это утверждение (гипотезу), называются критериями.
. Способы, позволяющие проверить это утверждение (гипотезу), называются критериями.
2.1 Критерий Колмогорова
Этот критерий основывается на максимальном значении модуля разности между статистической функцией распределения  и теоретической функцией распределения
и теоретической функцией распределения  :
:

А.Н. Колмогоров доказал, что для любой непрерывной функции распределения  вероятность неравенства
вероятность неравенства

при неограниченном возрастании  стремится к пределу
стремится к пределу
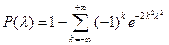
Значения этих вероятностей для различных значений 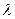 приведены в таблице 5.
приведены в таблице 5.
Таблица 5
| 
| 
| 
| 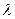
| 
|
| 0,000 | 1,000 | 0,700 | 0,711 | 1,400 | 0,040 |
| 0,100 | 1,000 | 0,800 | 0,544 | 1,500 | 0,022 |
| 0,200 | 1,000 | 0,900 | 0,393 | 1,600 | 0,012 |
| 0,300 | 1,000 | 1,000 | 0,270 | 1,700 | 0,006 |
| 0,400 | 0,997 | 1,100 | 0,178 | 1,800 | 0,003 |
| 0,500 | 0,964 | 1,200 | 0,112 | 1,900 | 0,002 |
| 0,600 | 0,864 | 1,300 | 0,068 | 2,000 | 0,001 |
Покажем, как работает критерий Колмогорова на примере конкретной задачи
Задача 4
Используя данные задачи 3, проверить гипотезу о том, что выборка значений случайной величины произведена из нормального распределения  .
.
Решение.
В таблице 3 сосчитано значение  для этой выборки:
для этой выборки:

| 0,107917 |
Вычислим 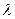 :
:

Интерполируя по таблице 5, находим  . Эта вероятность довольно велика, поэтому можно считать, что высказанная гипотеза не противоречит опытным данным. Если бы вычисленное значение оказалось порядка 0,01, то мы бы отвергли эту гипотезу на уровне значимости 0,05, так как при таком уровне значимости мы считаем все события, вероятность которых меньше 0,05 практически невозможными.
. Эта вероятность довольно велика, поэтому можно считать, что высказанная гипотеза не противоречит опытным данным. Если бы вычисленное значение оказалось порядка 0,01, то мы бы отвергли эту гипотезу на уровне значимости 0,05, так как при таком уровне значимости мы считаем все события, вероятность которых меньше 0,05 практически невозможными.
2.2. Критерий хи-квадрат.
Другим критерием, позволяющим проверить соответствие теоретической и статистической функции распределения, является критерий хи-квадрат, который основан на статистике (функции наблюденных значений):
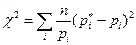
Это выражение удобно переписать в другом виде:
 .
.
Последнее выражение более удобно для вычислений.
Здесь, как и прежде,  - число наблюдений, попавших в
- число наблюдений, попавших в  - й разряд, а
- й разряд, а  - теоретическая вероятность попадания в
- теоретическая вероятность попадания в  - й разряд согласно функции распределения
- й разряд согласно функции распределения  случайной величины
случайной величины  .
.
К. Пирсон доказал, что при неограниченном увеличении числа опытов  и для любой функции
и для любой функции  распределение статистики
распределение статистики  стремится к одному и тому же пределу, именно функции распределения хи-квадрат с
стремится к одному и тому же пределу, именно функции распределения хи-квадрат с 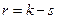 степенями свободы. Степени свободы это линейные ограничения, наложенные на частоты
степенями свободы. Степени свободы это линейные ограничения, наложенные на частоты  . Например, одно ограничение есть всегда:
. Например, одно ограничение есть всегда:
 .
.
Если других ограничений нет, то число степеней, свободы равно 1, а  .
.
могут быть еще ограничения, обусловленные оценками неизвестных параметров. Этот случай мы рассмотрим несколько позже.
Для распределения  составлены специальные таблицы, оно также включено в состав математического обеспечения многих программных продуктов, в частности, Excel.
составлены специальные таблицы, оно также включено в состав математического обеспечения многих программных продуктов, в частности, Excel.
Рассмотрим применение критерия  на примере задачи.
на примере задачи.
Задача 5
Используя данные задачи 3, проверить по критерию  гипотезу о том, что выборка значений случайной величины произведена из нормального распределения
гипотезу о том, что выборка значений случайной величины произведена из нормального распределения  .
.
Решение.
Исходим из данных таблицы 3. Для применения критерия  , требуется, чтобы количество наблюдений в разряде было не менее 5. Поэтому объединяем 1 и 2 разряды, а также 8, 9 и 10 разряды таблицы 3. В результате приходим к таблице 6. В новой таблице будет 7 разрядов, причем
, требуется, чтобы количество наблюдений в разряде было не менее 5. Поэтому объединяем 1 и 2 разряды, а также 8, 9 и 10 разряды таблицы 3. В результате приходим к таблице 6. В новой таблице будет 7 разрядов, причем 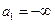 , а
, а  , так как теоретически нормально распределенная случайная величина может принимать любые значения на числовой прямой.
, так как теоретически нормально распределенная случайная величина может принимать любые значения на числовой прямой.
В таблице обозначено:
 - значение функции стандартного распределения в точке
- значение функции стандартного распределения в точке 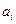 , а
, а

В правом нижнем углу желтым цветом выделено значение статистики  и вероятность наблюдать такое или большее значение за счет случайных отклонений. Как видим, вероятность довольно большая, поэтому нет оснований отвергать проверяемую гипотезу. Заметим, однако, что эта вероятность несколько меньше, чем для критерия Колмогорова.
и вероятность наблюдать такое или большее значение за счет случайных отклонений. Как видим, вероятность довольно большая, поэтому нет оснований отвергать проверяемую гипотезу. Заметим, однако, что эта вероятность несколько меньше, чем для критерия Колмогорова.
Таблица 6

| 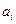
| 
| 
| 
| 
| 
| 
|
| -∞ | 0,0000 | ||||||
| -1,3663 | 0,0859 | 0,0859 | 8,59 | 3,41 | 1,3522 | ||
| -0,8463 | 0,1987 | 0,1128 | 11,28 | -1,28 | 0,1445 | ||
| -0,3263 | 0,3721 | 0,1734 | 17,34 | 8,66 | 4,3248 | ||
| 0,1937 | 0,5768 | 0,2047 | 20,47 | -2,47 | 0,2979 | ||
| 0,7137 | 0,7623 | 0,1855 | 18,55 | -5,55 | 1,6606 | ||
| 1,2337 | 0,8913 | 0,1291 | 12,91 | -3,91 | 1,1818 | ||
| +∞ | 1,0000 | 0,1087 | 10,87 | 1,13 | 0,1182 | ||
| ∑ | 1,0000 | 100,00 | 0,00 | 9,0801 | |||
| 0,1691 |
Рассмотрим теперь следующую задачу.
Задача 6
Используя данные задачи 3, проверить по критерию  гипотезу о том, что выборка значений случайной величины произведена из нормального распределения, параметры которого математическое ожидание
гипотезу о том, что выборка значений случайной величины произведена из нормального распределения, параметры которого математическое ожидание  и среднеквадратическое отклонение
и среднеквадратическое отклонение  нам неизвестны. Вместо них использовать оценки этих параметров, рассчитанные по выборке:
нам неизвестны. Вместо них использовать оценки этих параметров, рассчитанные по выборке:  и
и  . Методы расчета оценок параметров будут рассмотрены в следующем разделе.
. Методы расчета оценок параметров будут рассмотрены в следующем разделе.
Решение.
Построим таблицу 7, такую же, как таблица 6, но вместо функции  будем использовать функцию
будем использовать функцию 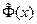 нормального распределения с параметрами
нормального распределения с параметрами  и
и  . Получим следующую таблицу.
. Получим следующую таблицу.
Таблица 7

| 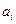
| 
| 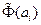
| 
| 
| 
| 
|
| -∞ | 0,0000 | ||||||
| -1,3663 | 0,1172 | 0,1172 | 11,72 | 0,28 | 0,0065 | ||
| -0,8463 | 0,2466 | 0,1294 | 12,94 | -2,94 | 0,6676 | ||
| -0,3263 | 0,4280 | 0,1814 | 18,14 | 7,86 | 3,4046 | ||
| 0,1937 | 0,6264 | 0,1984 | 19,84 | -1,84 | 0,1704 | ||
| 0,7137 | 0,7956 | 0,1692 | 16,92 | -3,92 | 0,9090 | ||
| 1,2337 | 0,9082 | 0,1126 | 11,26 | -2,26 | 0,4530 | ||
| +∞ | 1,0000 | 0,0918 | 9,18 | 2,82 | 0,8685 | ||
| ∑ | 1,0000 | 100,00 | 0,00 | 6,4796 | |||
| 0,1661 |
Новое значение статистики  , а вероятность такого же или большего отклонения, вычисленная при числе степеней свободы
, а вероятность такого же или большего отклонения, вычисленная при числе степеней свободы 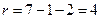 , оказалась равной 0,1661, т.е. почти такая же, как и в предыдущем случае. Поэтому мы с таким же уровнем доверия можем принять гипотезу о том, что данные извлечены из распределения
, оказалась равной 0,1661, т.е. почти такая же, как и в предыдущем случае. Поэтому мы с таким же уровнем доверия можем принять гипотезу о том, что данные извлечены из распределения  .
.
Задание к контрольной работе №1
Выполнить задачи 1-6 в соответствии с вариантом, который определяется по последней цифре в номере зачетной книжки студента.
Исходные данные для различных вариантов
Задача 1
Вариант 0 60 60 29 61 39 89 88 73 62 73
Вариант 1 66 63 46 52 39 54 57 59 35 55
Вариант 2 24 39 74 59 45 68 99 31 9 15
Вариант 3 103 97 83 104 108 111 98 102 77 68
Вариант 4 88 86 99 117 57 130 106 79 87 96
Вариант 5 126 144 142 113 117 135 122 143 106 129
Вариант 6 106 128 73 100 101 53 125 156 95 106
Вариант 7 81 98 82 88 122 73 78 88 87 119
Вариант 8 171 110 117 140 122 170 163 141 141 123
Вариант 9 125 133 113 149 123 108 117 132 102 108
Задачи 2-6
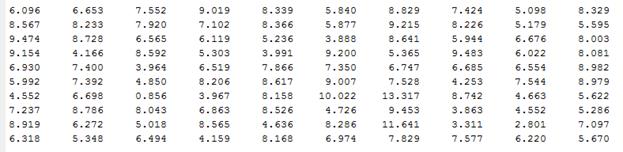
Вариант 0

Вариант 1

Вариант 2

Вариант 3

Вариант 4
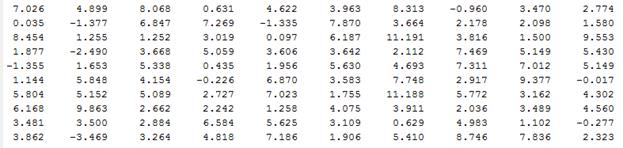
Вариант 5

Вариант 6

Вариант 7

Вариант 8

Вариант 9