1.6.1. Постановка задачи компьютерного моделирования.
Разработать алгоритмическое и программное обеспечение задачи имитации на ЭВМ процесса управления манипулятором в среде с неизвестными статическими препятствиями с использованием алгоритма двунаправленных графов.
· Необходимо написать функцию, реализующую алгоритм движения манипулятора в среде с известными препятствиями.
· Внедрить полученную функцию в алгоритм движения манипулятора в среде с неизвестными препятствиями.
· Визуализировать процесс движения манипулятора в среде с неизвестными препятствиями на декартовой системе координат и в системе обобщенных координат.
· Проанализировать время работы алгоритма от переменной delta – шаг дискретизации.
1.6.2. Анализ задачи моделирования.
При управлении манипулятором приходится решать следующую задачу: необходимо переместить манипулятор из одного положения в другое, т.е. стартовой конфигурации в целевую конфигурацию.
Сформулируем задачу движения манипулятора в среде с неизвестными препятствиями следующим образом: даны начальная конфигурация q 0 и целевая конфигурация q T, в рабочей области могут располагаться препятствия, но перед началом движения информация о наличии препятствий, их количестве, расположении и форме отсутствует. Требуется сделать так, чтобы манипулятор передвинулся из q 0 в q T.
Сделаем следующие допущения:
1) Положение, форма и размеры препятствий неизменны в течение всего времени движения манипулятора.
2) Заранее известно, что цель достижима (то есть известно, что в пространстве обобщенных координат можно найти линию, соединяющую q0 и q T и не налегающую ни на какое присутствующее в рабочей зоне препятствие).
3) Обобщенные координаты должны удовлетворять ограничениям.
a1 £ q (t) £ a2, (1.7)
где
a1 - вектор нижних ограничений на обобщенные координаты
a2 - вектор верхних ограничений на обобщенные координаты
1.6.3. Определение требований к исходной информации об объекте исследования и организация её сбора.
Манипулятор снабжен сенсорной системой, позволяющей определять, налегает ли манипулятор в текущей конфигурации на препятствия или нет, а также определять, имеются ли препятствия в небольшой окрестности текущей конфигурации. Устройство сенсорной системы в данной работе не рассматривается.
Возникает задача математического описания препятствий. Препятствия представляются следующим образом. Пусть манипулятор занимает некоторую конфигурацию q *. Если хотя бы одна точка манипулятора в данной конфигурации соприкасается с препятствиями, то считается, что эта конфигурация является запрещенной. Если ни одна точка манипулятора в данной конфигурации не соприкасается с препятствиями, то считается, что эта конфигурация является разрешенной. Спланированный маршрут движения манипулятора будет представлять собой некоторую линию в пространстве обобщенных координат. Эта линия не должна будет налегать на запрещенные точки q *.
1. Пусть манипулятор находится в q 0. Манипулятор с помощью своей сенсорной системы исследует небольшую r-окрестность в пространстве конфигураций около q 0 (рис. 1.3).
Рис. 1.3 Окрестность исследования манипулятора находящегося в q 0
Конфигурации, находящиеся в этой окрестности, образуют множество Y(q 0). Конфигурации, налегающие на препятствия, заносятся в множество запрещенных конфигураций Q(q 0). Конфигурации, не налегающие на препятствия, заносятся в множество разрешенных конфигураций Z(q 0). Манипулятор генерирует в пространстве обобщенных координат линию L(q 0, q T), соединяющую q 0 c q T, причем эта линия должна быть такой, что каждая точка этой линии удовлетворяет неравенствам (1.7) и не принадлежит множеству Q(q 0). Манипулятор начинает движение по этой линии и переходит в точку q 1ÎY(q 0). Следующий шаг опишем для общего случая, обозначив конфигурацию, в которой находится робот, через q n (n=1, 2,...).
2. Находясь в точке q nÎY(q n-1), манипулятор исследует r-окрестность около конфигурации q n и образует множества Y(q n), Q(q n) и Z(q n). При этом возможны две ситуации:
а) Линия L, по которой движется манипулятор, не пересекается с множеством Q(q n). В этом случае манипулятор собирается двигаться и дальше по этой линии;
б) Линия L, по которой движется манипулятор, пересекается с множеством Q(q n) (рис. 1.4).

Рис. 1.4 Совокупности разрешенных Z(qn) и запрещенных Q(qn) конфигураций r – окрестности манипулятора движущегося по линии L
Тогда манипулятор передвигается по линии в ту точку q s, следующая за которой уже принадлежит множеству Q(q n). Перейдя в точку q s, манипулятор генерирует новую линию L(q s, q T), не пересекающую множеств Q(q i), i=0, 1,..., n и собирается двигаться уже по новой линии.
3. Манипулятор по намеченной линии переходит в точку q n+1ÎY(q n), а алгоритм переходит на (п. 2), при этом индекс “n+1” заменяется на “n”.
1.6.4. Определение параметров и переменных модели.
Рассмотрим параметры модели для алгоритма, описывающего движение манипулятора в среде с известными препятствиями.
Все входные и выходные параметры представляют собой точку на двухмерной обобщенной системе координат, поэтому каждый параметр имеет составляющие x и y.
Входные параметры:
1. q 0(x,y), q T(x,y) – стартовая и целевая конфигурации;
2. mZap[z](x,y) - массив запрещенных точек;
3. z - количество запрещенных точек;
4. delta - шаг дискретизации;
5. qL(x,y) и qH(x,y) – вектора нижнего и верхнего ограничения на обобщенные координаты.
Выходные данные:
1. mRez[n](x,y) - массив точек конфигураций искомого пути;
2. n - количество точек конфигураций искомого пути.
1.6.5. Установление основного содержания модели.
Описание алгоритма двунаправленных графов [S.M. LaValle].
Известные препятствия задаются в виде геометрических фигур с n-вершинами, также известны координаты стартовой q 0 и целевой q T конфигураций (рис. 1.5).

Рис. 1.5 Пространство обобщенных координат. Препятствия 1 и 2, стартовая q 0 и целевая q T конфигурации.
1. Проводится отрезок из стартовой конфигурации q 0 в целевую q T. Если построенный отрезок не накладывается на препятствия, то этот отрезок есть искомый путь, а если отрезок налегает на препятствие, то делаем следующее.
1.1. Нумеруем вершины препятствий от 1 до n.
1.2. Соединяем точки всех вершин препятствий и точки стартовой и целевой конфигураций m-отрезками по принципу каждая с каждой.

Рис. 1.6 Стартовая точка q0 соединена со всеми вершинами препятствий
2. Отрезки, которые, накладываются на препятствия, мы не рассматриваем. Рассматриваются отрезки, которые либо не накладываются на препятствия, либо принадлежат граням препятствия (рис. 1.7).

Рис. 1.7 Жирные линии – рассматриваемые отрезки, пунктирные линии – не рассматриваемые отрезки.
3. Имеем k-путей из q 0 в q T.Сравниваем их по длине и выбираем кратчайший, т.е. получаем искомый путь (рис. 1.8).

Рис. 1.8 Искомый путь обозначен штрихпунктирной линией.
Описание модифицированного алгоритма движения манипулятора в среде с известными статическими препятствиями:
В описании алгоритма используются понятия:
· окрестная точка – точка, стоящая на расстоянии delta от текущей точки (рис. 1.9)

Рис. 1.9 Текущая точка qi имеет 8 окрестных точек.
· Область запрещенных точек – совокупность точек, каждая из которых имеет хотя бы одну соседнюю точку, отстоящую не более чем на delta.
1 Задаем входные параметры: q 0(x,y), q T(x,y), mZap[z](x,y), delta, qL(x,y) и qH(x,y) (рис. 1.10).

Рис. 1.10 Система обобщенных координат, содержащая три запрещенные точки mZap[0], mZap[1], mZap[2].
2 Получаем предварительный маршрут Pr[] – кратчайший путь от q 0 к q T без учета запрещенных точек следующим образом:
2.1 В начальный момент времени текущая конфигурация соответствует стартовой конфигурации q i = q 0.
2.2 Через точки q i и q T проводится прямая вида Ax+By+C=0.
2.3 Из окрестных точек q i выбирается q i+1 та, которая «максимально приближена» к прямой Ax+By+C=0 и «максимально приближена» к q T.
Расстояние от точки q i до точки q T определяется по формуле:
 (1)
(1)
Расстояние от точки до прямой Ax+By+C=0 определяется следующим образом:
коэффициенты прямой Ax+By+C=0:
A = Y q T - Y q 0,
B = X q 0 - X q T,
C = - X q 0*A - Y q 0*B,

если С > 0, то M=-M.
Расстояние от точки q i до прямой Ax+By+C=0 определяется по формуле:
P = A*M* X q i + B*M* Y q i + C*M; (2)
«Максимально приближенной» к прямой Ax+By+C=0 и «максимально приближенной» к q T является та окрестная точка, у которой значение Summa=P+D будет наименьшим.
2.4 Выбранная точка записывается в массив предварительного маршрута mPr[i+1]= q i+1 и становится текущей точкой q i= q i+1.
2.5 алгоритм переходит к п. 2.2 если текущая точка q i не достигла целевой q T.
Для данного случая получим (рис. 1.11).

Рис. 1.11 Система обобщенных координат. Точками 0-5 обозначены точки предварительного маршрута.
3 Сравниваем массив предварительного маршрута с массивом всех запрещенных точек. Если точки предварительного маршрута не налегают на запрещенные точки, т.е. манипулятор при движении из q 0 в q T не встречает препятствий, то массив предварительного маршрута mPr[] есть искомый массив mRez[] и алгоритм прекращает работу. В противном случае каждая запрещенная точка, на которую мы натолкнулись (в данном примере - mZap[2] и mZap[1]), считается точкой запрещенной области.
Из (рис. 1.11) видно, что точки 2 и 4 предварительного маршрута совпали с запрещенными точками mZap[2] и mZap[1] соответственно. Ни одна точка предварительного маршрута не натолкнулась на запрещенную точку mZap[0].
4 Формируются массивы областей запрещенных точек (в данном примере – массивы областей точек mZap[2] и mZap[1]). Для каждой из этих запрещенных точек осуществляется проверка окрестности на наличие окрестных запрещенных точек. Если такие точки есть, то они объединяются в массивы областей запрещенных точек.
5 Окружаем (помечаем) все запрещенные области разрешенными точками, т.е. берем каждую найденную запрещенную точку и окружаем ее разрешенными точками так, как показано на (рис. 1.12). Формируем массив разрешенных точек для каждой области запрещенных точек.

Рис. 1.12 Запрещенная точка MZap[2] окружена разрешенными точками 2.1, 2.2, 2.3, 2.4.
На этом этапе подготовка к движению манипулятора закончена.
6 Осуществляем движение из q 0 в q T по точкам предварительного маршрута:
6.1 q 0 принимается текущей точкой q i = q 0.
6.2 движемся по предварительному маршруту, записывая текущие точки в массив искомого пути mRez[i]=qi до столкновения с запрещенной областью или достижения целевой точки q T.
6.3 Совершаем обход запрещенной области только по разрешенным точкам этой области.
6.4 Обход осуществляется из точки прямого пути(где мы “попали в препятствие”) в точку прямого пути (где мы “покинули препятствие”) по двум направлениям (т.к. препятствие можно обойти с двух сторон) из которых выбирается кратчайший или если оба пути равны, то выбирается любой и записывается в mRez[].
6.5 Возобновляем движение по предварительному маршруту до столкновения со следующей запрещенной областью или достижения целевой точки q T, т.е. переходим к п.6.2
6.6 Алгоритм прекращает работу, если текущая конфигурация q i достигла целевой q T (рис. 1.13).
6.6.6.2м ющей движение по предварительному маршруту.ано нарисапрещенных точек

Рис. 1.13 Система обобщенных координат. Точками 0-5 обозначены точки искомого пути mRez[6].
1.6.6. Построение логической схемы.

Рис. 1.14 Логическая схема работы алгоритма в известной среде

Рис. 1.15 Логическая схема работы алгоритма в неизвестной среде
1.6.7. Проверка достоверности модели системы.
Важной характеристикой полученной модели является то, что алгоритм гарантирует достижение цели, в случае, если такой путь имеется. Не достижение цели возможно только при зацикливании алгоритма, т.е. манипулятор возвращается в «старую» точку имея ту же информацию о среде которую он имел попадая в эту точку первый раз.
В нашем случае манипулятор имеет достаточную информацию о среде еще до начала своего движения, что полностью исключает зацикливание алгоритма.
1.6.8. Выбор вычислительных средств для моделирования.
Не существует абсолютно совершенных языков программирования. Дело в том, что различные задачи требуют различных решений. При выборе языка программирования программист должен исходить из того, какие именно задачи он собирается решать с помощью своей программы. От правильного выбора языка программирования, в конечном счете, зависит успех всего проекта.
К наиболее перспективным языкам программирования, на базе которых возможна реализация специализированных операционных систем, работающих в реальном масштабе, времени можно отнести C, C++, Pascal.
Для решения выше поставленной задачи потребуется ряд основных параметров, по которым будем осуществлять выбор наиболее подходящего языка программирования (табл. 1.2).
Таблица 1.2
| № | Название параметра | С++ | Pascal |
| Цикл с параметром (for), шаг 1 | P | P | |
| Цикл с параметром (for), любой шаг | P | ||
| Выход, повтор цикла | P | P | |
| Операторы new, delete для выделения и освобождения дин. памяти | P | P | |
| Параметр «неограниченный массив» | P | ||
| Возможность определить размер параметра массива | P | ||
| Массив с переменной границей | P | ||
| Указатель | P | P | |
| Множество | P | ||
| Булевский тип | P | P | |
| Контроль границ индекса массивов | |||
| Импорт модулей | P | P | |
| Экспорт идентификаторов | P | P | |
| Ограничение видимости | P | ||
| Приоритеты логических операций | P | ||
| Операции разыменования | P | P | |
| Адресная арифметика | P | ||
| Итог: |
ВЫВОДЫ:
Главный вывод, который можно сделать на основе изложенного материала – несомненное сходство языков программирования в основных компонентах, таких, как набор операторов, конструктор типов, механизм процедур и ООП. Различия проявляются только в деталях. На основании проведенной экспертизы получили, что C++ более подходящий по параметрам, чем Pascal. Одновременно с этим С++ является языком достаточно низкого уровня, скорость выполнения программ на языке С++ соизмерима со скоростью их ассемблерных аналогов. Для программирования алгоритма выберем программу Borland C++ v5.01. Визуализацию работы алгоритма и движение манипулятора выполним на совместимом с Borland C++ v5.01 - Borland C++ Builder v6.0.
1.6.9. Проведение программирования.
Программирование алгоритма для известной среды состоит из пяти этапов изображенных на логической схеме (рис. 1.14). Текст программы представлен в (прил. 2). Программирование алгоритма для неизвестной среды состоит из четырех основных этапов изображенных на логической схеме (рис. 1.15).
1.6.10. Проверка достоверности программы.
Для случая, представленного в (прил. 1) c шаг разбиения delta = 120 программа полностью выполняет поставленную задачу по нахождению маршрута от q0 к qT(рис. 1.16).

Рис 1.16 Работа алгоритма в системе обобщенных координат при delta=120. По осям Ох и ОУ откладывается углы φ1 и φ2 (в градусах).
· q0 – стартовая конфигурация
· qT – целевая конфигурация
· 1…24 – промежуточные конфигурации
· – запрещенные конфигурации
В программе есть недостаток. Программа работает для delta > 50. При delta < 50, т.е. когда шаг дискретизации достаточно мал, возникает большое количество запрещенных и промежуточных конфигураций, что приводит к переполнению программных и аппаратных ресурсов.
1.6.11. Анализ полученных результатов моделирования системы.
Сравним результаты полученные алгоритмом Nilson для ситуации приведенной в (прил. 1) с алгоритмом разработанным в данной дипломной работе (табл.1.3).
Таблица 1.3
| № | delta, ˚ | Количество дискретов | Время, секунд | |
| Nilson | Данный алгоритм | |||
| меньше 1 | ||||
| меньше 1 | ||||
| меньше 1 | ||||
| меньше 1 | ||||
| 4.5 | - | |||
| - | ||||
| - | ||||
| - | ||||
| 1.5 | - |
Как видно из приведенных выше таблиц, разработанный алгоритм показал лучшие результаты по быстродействию по сравнению с ранее разработанным программным обеспечением при тестировании его на двухзвенном манипуляторе с вращательными кинематическими парами 5-ого класса при шаге дискретизации delta > 50. Время работы алгоритма удовлетворяет поставленной задаче.
Для повышения эффективности алгоритма данный алгоритм для двухмерного случая можно адаптировать в n-мерный не внося значительных изменений, но при этом значительно увеличится программная часть, реализующая алгоритм, что потребует гораздо больших аппаратных ресурсов. С многомерностью алгоритма увеличится количество возможных путей обхода препятствий и вырастит сложность их описания, а значит и время из расчета, что нежелательно. Во избежание этого и повышения эффективности программного обеспечения следует исключать наименее эффективные пути обхода, постараться упростить описание препятствий и следить за переполнением аппаратных ресурсов.
1.6.12. Руководство пользователя
Минимальные системные требования для работоспособности программы:
· OS Windows 98/Me/2000/XP (или любая другая способная работать с 32 – разрядными приложениями)
· CPU Intel/AMD 1500 Гц
· RAM 256 MB
Программа написана на языке программирования C++ Builder 6. Для правильной работы программы необходимы следующие файлы.
Исходные файлы проекта:
· Probot.h, Urobot.h, Urobot2.h – заглавные файлы
· Probot.cpp, Urobot.cpp,Urobot2.h - файл содержащий функцию реализующую алгоритм движения манипулятора в неизвестной среде
· Probot.res, Probot.def – файлы формы
· Finish_optimized.cpp – файл содержащий функцию реализующую алгоритм движения манипулятора в известной среде.
Файл с откомпилированной программой:
· Probot.exe – файл программы не требующая вышеперечисленных файлов, а так же C++ Builder.
Вышеуказанные файлы, кроме Probot.exe, должны размещаться в одной папке (желательно разместить файлы в папке C:\Program Files\Borland\CBuilder6\Projects\ваша_папка).
Программа представляет собой 32 - разрядный exe файл. Запускаем файл Robot.exe. На появившейся форме задаем входные параметры:
1. q 0(x,y), q T(x,y) – стартовая и целевая конфигурации;
2. delta - шаг дискретизации или количество разбиений;
3. интервал прорисовки в мс.
Для принятия вышеприведенных параметров нажимаем кнопку "применить". На экране появляется форма, на которой изображена декартовая система координат с препятствиями и стартовой и целевой конфигурациями.
Кнопка "пуск" запускает алгоритм движения манипулятора в неизвестной среде со статическими препятствиями. Если все данные введены правильно, то на декартовой системе координат манипулятор будет осуществлять движение от стартовой конфигурации к целевой, в системе обобщенных координат будет видно движение точки также от стартовой конфигурации к целевой. Нажатием кнопки "пауза" можно прервать движение манипулятора, а при повторном нажатии возобновить движение. В приведенном в нижнем правом углу главной формы список отображает координаты точек искомого маршрута. Выше списка записывается суммарное время работы алгоритма.
Нажимать клавиши программы можно только в той последовательности, которая приведена в руководстве пользователя.
Экономическая часть
Оценка совокупной стоимости программного продукта очень важна для рационального распределения финансовых ресурсов. Нахождение путей снижения издержек. В случае обновления или совершенствования программы, приведенные ниже расчеты помогут сравнить затраченные ресурсы, тем самым оценить эффективность программы по сравнению с уже имеющейся.
1.7.1. Расчет затрат на разработку программы
Расчет затрат на разработку программного продукта производится по следующей формуле:
 ,
,
где S – затраты на программу;
n – количество разработчиков;
t р – время, затрачиваемое на разработку данной программы конкретным программистом, чел-мес;
З ро – основная заработная плата программиста с учетом районного коэффициента, руб./мес.;
К рд – коэффициент, учитывающий дополнительную заработную плату разработчика программы, в долях к основной заработной плате; (В состав дополнительной з/платы входит оплата очередного, учебного отпуска, выслуги лет, районный коэффициент – 30%).
K рс – коэффициент, учитывающий отчисления на социальные нужды, в долях к сумме основной и дополнительной заработных плат;
К н – коэффициент, учитывающий накладные расходы организации, в которой разрабатывается данная программа (от 2,0 до 4,0);
t мо – машинное время ЭВМ для отладки программы одним программистом, машино-часы;
е р – эксплуатационные расходы на 1час машинного времени, руб./машино-ч.
Заработная плата складывается из стипендии студентов, выполняющих дипломную работу, оплаты работы дипломного руководителя, оплаты консультационных часов. Стипендия одного дипломника составляет 1000 руб. Руководителю оплачивается 20 академических часов в соответствии с разрядом дипломного руководителя (1 час – 80 руб). На консультации отводится 6 академических часов.
n = 1
t p = 4 мес.;
Зро = 1000 руб./мес.;
t мо = 1 час.;
К рд = 0,6;
К рс = 0,358;
К н = 2;
е р = 2,9 руб./час.
Сумма затрат на разработку программы составляет:
S = 4´1000´[(1+0,6)´(1+0,358)+2]+1´2,9 = 16694,1 руб.
Расчет стоимости программы «нормативной документации» произведём по формуле:
Z = S + 0,2 × S
где Z – стоимость программы.
Z = 16694,1+16694,1´0,2 = 20032,92 руб.
1.7.2. Расчет капиталовложений, связанный с использованием разработанной программы
Расчет основных кап. вложений будем производить по формуле:
К = К об + К зд + К пр,
где К – капитальные вложения в ЭВМ, для которой предназначена данная программа, руб./год;
К об – стоимость оборудования, руб.;
К зд – стоимость производственных помещений необходимых для машинной обработки данных, руб.;
К пр – предпроизводственные затраты, руб.
Кафедра предоставляет студентам ЭВМ Коб = 20000, но т.к. ЭВМ принадлежат кафедре студентам не нужно оплачивать ее стоимость, значит берем Коб = 0. ЭВМ размещаются на рабочих местах специалистов и имеют в своем составе разнообразные прикладные системы. Следовательно, при использовании ЭВМ К зд и К пр не требуются.
К = 0 руб.
В данной дипломной работе расчет дополнительных капвложений не требуется.
1.7.3. Расчет эксплуатационных расходов связанных с использованием разработанной программы
Расчет эксплуатационных затрат на обработку данных программы будем производить по формуле:
Е = Зо + Зд + Зс + Аоб + Вм + Вэ + Азд,
где Е – эксплуатационные расходы;
Зо – основная заработная плата обслуживающего персонала, руб./год;
Зд – дополнительная заработная плата обслуживающего персонала, руб./год;
Зс – отчисления на социальные нужды, руб./год;
Аоб – амортизационные отчисления на оборудование, руб./год;
Вм – затраты на основные и вспомогательные материалы, руб./год;
Вэ – затраты на электроэнергию (исходя из стоимости 0,28 руб./кВт);
Азд – амортизационные отчисления на здания, руб./год.
Так как данная программа предназначена для АРМ, то не требуется дополнительного обслуживающего персонала, и так же не требуется амортизационных отчислений на здания, потому что компьютер устанавливается непосредственно на рабочее место.
Для работы на ЭВМ не требуется обслуживающий персонал, устанавливаются они на рабочих местах специалистов, поэтому Зо, Зд, Зс, Азд, в этом случае не требуются и равны нулю.
Затраты на электроэнергию Bэ определяются исходя из годового фонда рабочего времени Т р и потребляемой ЭВМ мощности (250 Вт).
Затраченное машинное время в часах определяется следующим образом:
Т р = N × Т ср × n,
где Т ср – среднесуточная загрузка оборудования (6 час.);
N – среднее количество дней работы ЭВМ в течение месяца;
n – количество рабочих месяцев.
N = 253,3;
n = 4;
Т р = 22 ´ 6 ´ 4 = 528 час.
Вэ = 528 ´ 0,28 ´ 0,25 = 36,96 руб./год.
В укрупненных расчетах годовые затраты на основные и вспомогательные материалы (гибкие диски, бумага) определяются в размере 1% от стоимости основного оборудования.
Вмг = 0,01 × Kоб = 0,01 × 20000 = 200 руб/год.
Так как работа производится не целый год, то
 .
.
Величина  рассчитывается по следующей формуле:
рассчитывается по следующей формуле:
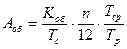 ,
,
где  – срок службы оборудования (для данного оборудования
– срок службы оборудования (для данного оборудования  = 6 лет);
= 6 лет);
 – общее время работы компьютера за день (8 часов).
– общее время работы компьютера за день (8 часов).
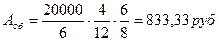
Эксплуатационные затраты на обработку данных программы:
Е = 833,33 +66,67+36,96= 936,96 руб./год.
Расчет эксплуатационных расходов на 1 час машинного времени производим по формуле:
 ,
,
 .
.






