Позиционные системы счисления
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения:
700 + 50 + 7 + 0,7 = 7•102 + 5•101 + 7•100 + 7•10-1 = 757,7.
Любая позиционная СС характеризуется своим основанием.
Основание позиционной СС — это количество различных знаков или символов, используемых для изображения цифр в данной системе.
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения:
an-1 qn-1 + an-2 qn-2+... + a1 q1 + a0 q0 + a-1 q-1 +... + a-m q-m,
где ai – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.
Двоичная система счисления. Перевод из двоичной системы счисления в десятичную систему счисления и обратно.
Несмотря на то, что мы привыкли работать с десятичной системой счисления, с технической точки зрения она неудобна, т.к. в электрических цепях компьютера требовалось бы иметь одновременно десять различных сигналов. Чем меньше различных сигналов в электрических цепях, тем проще микросхемы. Наименьшее основание, которое может быть у позиционных систем счисления, это – двойка. Именно по этому двоичная система счисления используется в вычислительной технике.
Двоичная система счисления — позиционная система счисления с основанием 2.
Уже отмечалась выше о записи двоичного числа в виде суммы степеней основания системы счисления, то есть степеней двойки. Сделав такую запись, надо подсчитать десятичное значение полученной суммы.
Например: переведем число из двоичной системы счисления в десятичную систему, разбив его на разряды:
3 2 1 0
10112 = 1*23+0*22+1*21+1*20=8+0+2+1 = 8+0+2+1 = 1110
Задание 2. Переведите следующие числа из двоичной системы счисления в десятичную систему счисления:
1) 1012 =
2) 10012 =
3) 10001012 =
4) 11001102 =
5) 111000112 =
Алгоритм перевода чисел из десятичной системы счисления в двоичную систему счисления:
1) разделить число на 2 и зафиксировать остаток;
2) если частное от деления не равно 0, повторить пункт 1) для частного;
3) если частное от деления равно 0, записать все полученные остатки справа налево.
Например: перевести число 2510 в двоичную систему счисления.
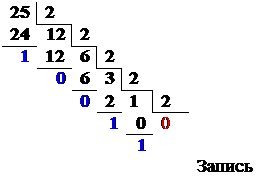
Таким образом, 2510 = 110012
Задание 3. Перевести следующие числа из десятичной системы счисления в двоичную систему счисления:
1) 3710 =
2) 5910 =
3) 11610 =
4) 24510 =
5) 56410 =
Системы счисления, используемые в вычислительной технике
Восьмеричная система счисления. Алфавит восьмеричной системы счисления состоит из 8 цифр: 0,1,2,3,4,5,6,7. 8 — это 2 в третьей степени. При переводе в восьмеричную систему двоичное число из трех записывается одной цифрой.
| Восьмеричная запись | Двоичное представление |
Впереди стоящий 0 ничего не значит.
Для перевода из двоичной системы счисления в восьмеричную систему счисления число, записанное в двоичной системе, делим на триады справа налево, и заменяем каждую группу одной восьмеричной цифрой.
Например: перевести число 110111000112 в восьмеричную систему счисления.
110111000112 = 011 011 100 011
 | |||||||||
 |  |  |  |
3 3 4 3
и получим, что 110111000112 = 3343.
Задание 4. Перевести следующие числа из двоичной системы счисления в восьмеричную систему счисления:
1) 100010010112 =
2) 1001100110012 =
3) 1011011110102 =
4) 1001111001002 =
Для перевода числа из восьмеричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную систему, представив каждую цифру в виде триады.
Например. Перевести число 3568 в двоичную систему счисления.
 3568 = 3 5 6
3568 = 3 5 6
011 101 110
получается, что 3568 = 111011102
Задание 5. Перевести следующие числа из восьмеричной системы счисления в двоичную систему счисления:
1) 2678 =
2) 7418 =
3) 6528 =
4) 5438 =
Шестнадцатеричная система счисления. Для первых 10 из 16 шестнадцатеричных цифр используются привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а для остальных используют первые буквы латинского алфавита A (10), B (11), C (12), D (13), E (14), F (15).
Число 16 – это 2 в четвертой степени. При переводе из двоичной системы в шестнадцатеричную систему счисления двоичное число из 4-х цифр кодируется числом из одной цифры в шестнадцатеричной системе.
| Двоичное представление | Шестнадцатеричная запись |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
Для перевода числа из шестнадцатеричной системы в двоичную достаточно заменить каждую цифру на ее эквивалент в двоичной системе счисления, представив каждую цифру в виде сочетания четырех 1 и 0.
Например: Перевести число А0F16 в двоичную систему счисления.
А0F16 = А 0 F
 |  |  |
1010 0000 1111
получается, что А0F16 = 1010000011112
Задание 6. Перевести следующие числа из шестнадцатеричной системы счисления в двоичную систему счисления:
1) A216 =
2) В6С16 =
3) D9716 =
4) E8F016 =
Для перевода из двоичной системы в шестнадцатеричную необходимо разбить число, записанное в двоичной системе на группы по 4 справа налево, заменив каждую группу одной шестнадцатеричной цифрой.
Например. Перевести число 1101101011012 в шестнадцатеричную систему счисления.
 1101101011012 = 1101 1010 1101
1101101011012 = 1101 1010 1101
D А D
получается, что 1101101011012 = DAD16
Задание 7. Перевести следующие числа из двоичной системы счисления в шестнадцатеричную систему счисления.
1) 1001101110112 =
2) 100000100102 =
3) 1011110010012 =
4) 1111000011102 =
1.3. Двоичная арифметика.
Все операции над числами в двоичной СС, точно так же как и в десятичной, проводятся поразрядно. Приведем операции сложения и умножения, соответствующие примеры.
| Операция сложения: | 0 + 0 = 0 |
| 0 + 1 = 1 | |
| 1 + 0 = 1 | |
| 1 + 1 = 10 | |
| Операция умножения | 0 * 0 = 0 |
| 0 * 1 = 0 | |
| 1 * 0 = 0 | |
| 1 * 1 = 1 | |
| Операция вычитания | 0 - 0 = 0 |
| 1 – 0 = 1 | |
| 1 – 1 = 0 | |
| 0 – 1 = 11(заем из старшего разряда) |
Например. Сложить числа 101100 и 1011.
+ 1011
Например. Умножить числа 101 и 11.
*11
+101
Задание 8. Сложить следующие двоичные числа:
1) 1001112 + 10112 =
2) 1100112 + 110112 =
Задание 9. Умножить следующие двоичные числа:
1) 110012 * 10012 =
2) 101112* 110112=
Задание 10. Вычесть двоичные числа:
1) 10010 – 1001 =
2) 101,011 – 1,110 =
3) 101,011 – 11,101 =
Контрольные вопросы.
1. Что такое система счисления?
2. Какие типы систем счисления вы знаете?
3. Что такое основа позиционной системы счисления?
4. Какая система счисления используется для представления информации в компьютере? Почему?
Домашнее задание
1. Перевести числа из восьмеричной системы счисления в двоичную систему:
168 =
558 =
2. Перевести числа из шестнадцатеричной системы счисления в двоичную систему:
34А16 =
3. Перевести числа из двоичной системы счисления в шестнадцатеричную систему счисления:
1001110011112 =
1101010101012 =
4. Перевести числа из двоичной системы счисления в восьмеричную систему:
1111011112 =
101101012 =
5. Перевести числа из двоичной системы счисления в десятичную систему:
101102 =
10101012 =
6. Перевести числа из десятичной системы счисления в двоичную систему:
12310 =
4510 =
7. Перевести из пятеричной системы счисления в девятеричную:
4325 =
23015 =
8. Сложить двоичные числа:
10110112 + 10110112 =
111112 + 1000012 =
9. Вычесть двоичные числа:
111001 – 111 =
11101,001 – 1111,11 =
10. Умножить двоичные числа:
1012 * 11012 =
10102 * 11112 =
11.Выполнить сложение чисел:
547 + 237 =
1234 + 2014 =






