Изучение рабочего процесса дозатора

ВЯТСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ

Инженерный факультет

Кафедра технологического и энергетического оборудования

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторной работе № 11

«Изучение и оптимизация рабочего процесса дозатора и смесителя кормов»

Киров - 2007

УЧЕБНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА № 11

(8 часов)

Тема: «ИЗУЧЕНИЕ И ОПТИМИЗАЦИЯ РАБОЧЕГО ПРОЦЕССА ДОЗАТОРА И СМЕСИТЕЛЯ КОРМОВ»

Цель работы: Определить характеристики процессов дозирования и смешивания кормов. Подтвердить теоретические предпосылки процесса смешивания и определить оптимальное значение основных факторов процесса смешивания.

НЕОБХОДИМОЕ ОБОРУДОВАНИЕ

1. Смеситель;

2. Дозатор;

3. Секундомер;

4. Тахометр;

5. Весы;

6. Сито;

7. Тара.

СОДЕРЖАНИЕ РАБОТЫ

Дозирование кормов

На процесс дозирования оказывают влияние физико-механические свойства кормов: насыпная плотность, размеры частиц, угол естественного откоса, влажность, слеживаемость, комкуемость (склонность к комкообразованию), конструктивные особенности дозирующего устройства и другие факторы.

Непрерывное дозирование состоит в обеспечении выдачи заданного количества материала в единицу времени. Однако реальный процесс сопряжен с отклонениями (погрешностями) от заданной величины, то есть является случайным.

Среднее значение абсолютной погрешности дозатора

(1)

где 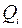- действительная подача или расход материала в –ом измерении, выраженная в м³/с (объемный расход) или кг/с (массовый расход);

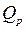- расчетное значение подачи; 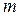- число измерений.

Показателем относительной погрешности дозирующего устройства служит коэффициент вариации, %

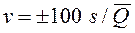, (2)

где 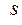- средняя квадратическая погрешность;

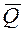- среднее значение подачи дозатора в 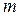пробах.

Поток корма, выдаваемый дозатором, можно представить как случайный процесс в виде реализации подачи во времени.

Показатели погрешности, выраженный в виде числовых характеристик случайной величины, не дают объективной оценки точности дозирования в общем случае, так как их значения зависят от числа проб и абсолютной величины среднего значения, изменяются во времени и не отражают внутренней структуры процесса.

Наиболее объективно характеризовать качество процесса позволяет система оценки технологических допусков машин и поточных линий, которая применительно к дозаторам и питателям непрерывного действия может быть выражена в следующем.

В общем случае реализацию выходного процесса, определяющего эффективность функционирования машины или линии по какому-либо показателю, можно представить в виде

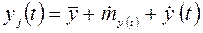(3)

где 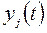- любая реализация случайного процесса;

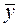- среднее значение процесса (общее);

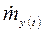- центрированная составляющая низкочастотной части процесса (отклонение от среднего значения);

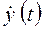- отклонение случайного процесса от центрированной составляющей (центрированный процесс).

В качестве критерия оптимизации по оценке подачи дозирующего устройства можно назначить вероятность пребывания случайного процесса в поле допуска 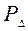. При этом чем больше 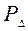, тем лучше и равномернее подача корма.

Физический смысл вероятности 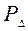заключается в том, что она показывает долю времени реализации, в течение которой процесс находится в поле допуска.

Исследованиями процессов дозирования и раздачи кормов доказано, что отклонения от среднего значения конкретной дозы определяются по нормальному закону, поэтому допуск симметричен относительно среднего значения.

Аналитически вероятность

, (4)

где 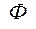- функция Лапласа, принимается по таблицам в зависимости от (см. приложение);

цифра 2 означает симметричность допуска относительно среднего значения подачи;

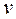- среднее квадратичное отклонение случайного процесса за время реализации, отнесенное к среднему значению, то есть .

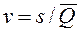Среднее квадратическое отклонение 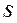рекомендуется определять по формуле

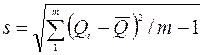(5)

где 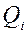- текущее значение подачи;

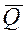- среднее значение подачи;

- число ординат, принятое для расчета (число измерений).

Предельные отклонения подачи дозатора (максимальное 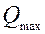и минимальное 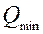) можно определить по правилу трех сигм:

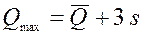и 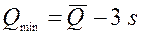, где - среднее значение подачи; 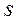- среднее квадратичное отклонение подачи. Это обеспечивает надежность выводов с вероятностью 0,9973.

Смешивание кормов

В результате смешивания первоначально находящиеся раздельно компоненты после равномерного распределения каждого из них в смешиваемом объеме материала образуют однородную смесь.

Устройства, в которых осуществляется процесс смешивания, называются смесителями, а их рабочие органы – мешалками.

Качество смешивания определяется рядом факторов, которые можно разделить на три группы:

- методы смешивания (распыливание, пересыпание, перелопачивание, наслаивание компонентов, смешивание в «кипящем слое»);

- конструктивные особенности смесителей и их режим работы (степень заполнения, скорость и характер циркуляции материала в смесителе, конструкция мешалок, частота их вращения);

- физико-механические характеристики смеси компонентов (соотношение компонентов, их гранулометрический состав, плотность, коэффициент внутреннего трения).

Чтобы оценивать качество смешивания одной случайной величиной, что математически значительно проще, смесь считают двухкомпонентной. Для этого выделяют из смеси один какой-то компонент, называемый контрольным (ключевым), а все остальные объединяют во второй условный компонент. По степени распределения контрольного компонента в массе судят о качестве смеси.

Количественной характеристикой завершенности процесса смешивания является степень однородности, представляющая собой отношение содержания контрольного компонента в анализируемой пробе к содержанию того же компонента в рецептурной смеси.

(6)

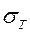- теоретическое среднее квадратическое отклонение.

Степень однородности изменяется от 0 до 1 и чем ближе к единице, тем лучше завершен процесс и качественнее смесь.

В качестве критерия оценки процесса смешивания можно использовать коэффициент неоднородности (вариации), выражаемый в %

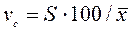, (7)

где 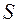- величина среднего квадратического отклонения контрольного компонента по данным опытов.

Значение 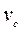=20% для большинства смесителей кормов оказывается достаточным.

Кинетика процесса смешивания, то есть развитие его во времени , зависит главным образом от конструкции смесителя.

Если проследить за смешиванием по показателю изменчивости 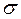(рисунок 1), то можно отметить три стадии развития процесса:

перемещение группы смежных частиц из одного места смеси в другое внедрением, вмятием, скольжением слоев – конвективное смешивание (участок I), которое протекает на уровне микрообъемов и почти не зависит от физико-механических свойств материалов;

постепенное перераспределение части различных компонентов через свежеобразованную границу их раздела – диффузионное смешивание (участок II), которое протекает на уровне микрообъемов;

сосредоточение частиц, имеющих одинаковую массу, в соответствующих местах смесителя под действием гравитационных или инерционных сил – сегрегация (участок III), которая по своему действию противоположна первым двум стадиям – одна ухудшает качество смеси.

Если участок 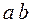представляет собой полосу допустимых значений показателя изменчивости, то в конце участка II процесс смешивания должен быть закончен, так как дальнейшее воздействие на материал не имеет смысла, и оптимальное время смешивания для данного смесителя и определенного вида материала находят экспериментально.

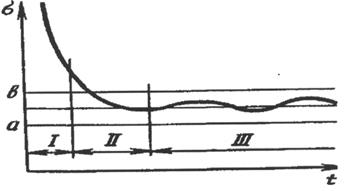
Рисунок 1 – Кинетика процесса смешивания

При работе большинства смесителей кормов периодического действия оптимальное время смешивания 8…12 мин. Для шнековых смесителей непрерывного действия при смешивании комбикормов достаточна длина шнека, равная 0,9…1 м.

Для оценки качества смешивания кормов наибольшее применение находит коэффициент вариации, физический смысл которого заключается в том, что он измеряет среднеквадратическое отклонение доли контрольного компонента в единицах среднего значения случайной величины.

Если при одном и том же качестве смешивания компонентов увеличивать дозу ввода контрольного компонента, то больше дозе будет соответствовать меньшее значение коэффициента вариации, то есть лучшее качество.

Как показали многочисленные исследования, закон распределения доли контрольного компонента в смеси по окончании процесса смешивания может быть биномиальным, пуассоновским и нормальным.

Пуассоновское распределение возникает тогда, когда доза ввода контрольного компонента очень мала – менее 0,1. При достаточно большом числе проб биномиальное распределение хорошо аппроксимируется нормальным. Поэтому, исходя из сущности процесса смешивания, его можно оценить статическими методами.

Предполагаем, что закон распределения частиц контрольного компонента в смеси нормальный. Задаемся предельным отклонением числа или доли частиц контрольного компонента 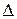, то среднего значения в пробах какого-либо сечения смесителя. Это предельное отклонение определяется, из зоотехнических условий на качество кормовой смеси.

В результате анализа 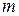проб получаем следующие значения доли частиц контрольного компонента ; и 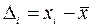(здесь - среднее значение доли частиц контрольного компонента в смеси, ).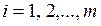

Пронормируем эти величины путем деления каждой на среднее квадратическое отклонение :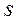

, , .

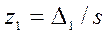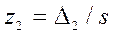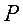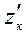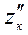Закон распределения случайных величин также будет нормальным. Тогда вероятность попадания числа частиц или доли частиц контрольного компонента в заданные пределы и определится из выражения

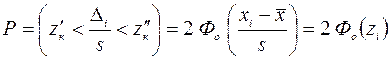, (8)

где - нормированная функция Лапласа (см. приложение).

Цифра 2 означает, что отклонение в обе стороны от среднего значения одинаковы.

На рисунке 2 показана кривая нормальной плотности 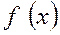нормированной случайной величины (число частиц контрольного компонента). Заштрихованные площади показывают суммарную долю частиц контрольного компонента, заключенную в заданных переделах.

Площадь под кривой нормального распределения равна единице и характеризует распределение всей совокупности частиц контрольного компонента. Если в качестве предельного размаха распределения принять значение 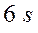, то вероятность нахождения доли частиц контрольного компонента

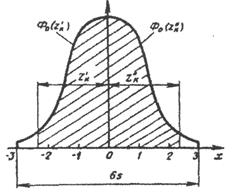
Рисунок 2 – Плотность вероятности нормального распределения

в пределах равна 0,9973, то есть из 10000 случаев отклонения превысит заданные пределы только в 27 случаях. Такое отклонение на практике можно считать невозможным. Тогда степень однородности смешивания можно задать в виде:

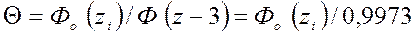, (9)

где 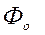- нормированная функция Лапласа.

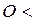Физический смысл заключается в том, что доля частиц контрольного компонента в смеси, которая находится в заданных пределах ; при этом ө 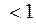. Предельному случаю полного смешивания соответствует значение ө .

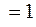Таким образом, степень однородности смешивания не зависит от дозы ввода контрольного компонента, а характеризуется лишь показателями неоднородности, полученными в результате смешивания, и может быть использована в качестве объективного критерия для сравнения различных режимов работы смесителя и разных типов смесителей.

Для изучения процессов дозирования и смешивания кормов разработана установка, которая представляет собой барабанный дозатор на базе катушечного аппарата зерновой сеялки, а в качестве смесителя использован шнек.

Установка предусматривает варьирования ряда конструктивных факторов: частоту вращения и шнека; степень открытия катушечного аппарата, угол наклона смесителя к горизонту. Предусмотрены по всей длине смесителя пробоотборные устройства.

Технологическая схема установки показана на рисунке 3.

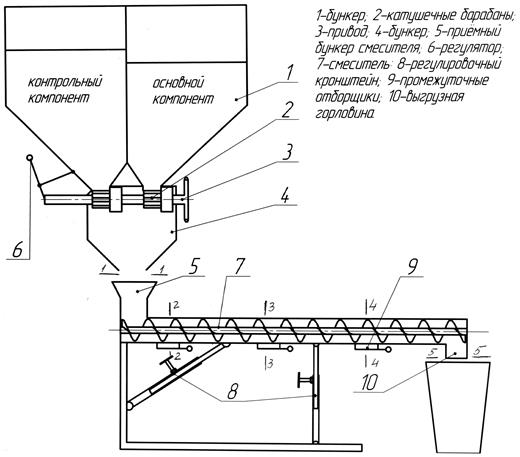
Рисунок 3 - Технологическая схема установки (дозатор-смеситель)

Она имеет общую раму, на которой смонтированы загрузочный бункер 1, разделенный на две части перегородкой для основного и контрольного компонентов. В днище бункера установлены катушечные барабаны 2 с приводом 3. При вращении барабанов, корм из бункера 1 поступает в бункер 4. Для изменения подачи дозирующих барабанов установлен регулятор 6, изменяющий длину активной части барабанов. В шнековом смесителе 7 для изменения угла наклона корпуса смесителя к горизонту, установлены регулировочные кронштейны 8. Для отбора проб предусмотрены отборщики 9. Цифрами 1-1, 2-2,…, 5-5 обозначены номера сечений, откуда отбираются пробы материала.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Изучение рабочего процесса дозатора

1.1. Засыпать в бункеры дозатора компоненты смеси и установить его на подачу компонентов (по заданию преподавателя). На пробоотборник дозатора установить полиэтиленовый пакет. Заслонку дозатора переключить на подачу в смеситель.

2. Запустить смеситель, затем дозатор и при установившемся режиме взять пробу с подачи дозатора в течении 10 с в трехкратной повторности. Результаты опытов занести в таблицу 1.1.

3. По результатам опытов рассчитать среднее значение подачи 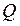, среднее квадратическое отклонение 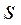по формуле (5), коэффициент вариации 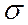по формуле (2), вероятность пребывания процесса в поле допуска 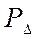по формуле (4). Допуск 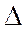принять по заданию преподавателя. Вычислить предельные отклонения подачи (максимальное 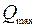и минимальное 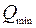) «по правилу трех сигм».

4. Сделать вывод о точности дозирования кормов изучаемого дозатора по коэффициенту вариации, считая достаточным его численное значение 20%.