105.1. Чему равен неопределенный интеграл 
.
В)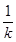 
, где u=kx+b
106.1. Найти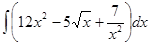 
B) 
107.1. Вычислить интеграл 
A) ln(x2+1)+C;
107.2. Вычислить интеграл 
B) 
;
108.1. Какой вид приобретет подынтегральная функция интеграла 
после осуществления замены переменных x=t2.
C) 
;
108.2. Какой вид приобретет подынтегральная функция интеграла 
после осуществления замены переменных x=t2.
E) 
;
108.3. Какой вид приобретет подынтегральная функция интеграла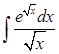 
после осуществления замены переменных x=t2.
B) 2 
;
109.1. Найти интеграл 
А)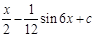 
;
109.2. Найти интеграл 
А) 
;
109.3. Вычислить неопределенный интеграл 
D) 
;
109.4. Вычислить неопределенный интеграл 
В) 
;
109.5. Вычислить неопределенный интеграл 
В) 
;
109.6. Вычислить неопределенный интеграл 
А) 
;
109.7. Вычислить неопределенный интеграл 
Е) 
;
109.8. Вычислить неопределенный интеграл 
В) 
;
109.9. Вычислить неопределенный интеграл 
D) 
;
109.10. Вычислить неопределенный интеграл 
А) 
;
109.11. 
Е) 
arc tg 
+C;
109.12. 
Е) tg3 х +C;
109.13. 
А) 2 
;
109.14.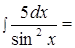 
В) –5 ctgx + C;
109.15. Вычислить интеграл 
С) 
;
109.16. Найти интеграл 
D) - 
;
109.17. Найти интеграл 
А) 
;
109.18. Найти интеграл 
А) 
;
109.19. Найти интеграл 
А) 
;
109.20. Найти интеграл 
А) 
;
109.21. Найти интеграл 
А) 
;
109.22. Найти интеграл 
А) 
;
109.23. Найти интеграл 
Е) 
;
109.24. Найти интеграл 
D)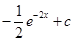 
;
109.25. Найти интеграл 
А) 
;
109.26. Найти интеграл 
С) 
;
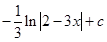109.27. Найти интеграл 
В) 
;
110.1. Какая из ниже перечисленных функций является первообразной функции f(x) = 
.
C) 2 
111.1. Для вычисления интеграла 
интегрированием по частям необходимо обозначить:
A) u=lnx, dv=x2dx
112.1. Формула Ньютона-Лейбница имеет вид
С) 
113.1. 
формула замены переменной в интеграле
А) определенном интеграле
114.1. Чему равен интеграл с одинаковыми пределами:
А) 
115.1. Формула интегрирования по частям в определенном интеграле имеет вид
С) 
116.1. Если функция f(x) – четная, то 
С) 
116.2. Если функция f(x) – нечетная, то
D) 
117.1. Вычислить интеграл 
A) 21
117.2. Вычислить определенный интеграл 
D) 
118.1. Геометрический смысл определенного интеграла:
А) 
= S - площадь плоской фигуры
119.1. Площадь поверхности, полученной от вращения вокруг оси OX кривой y=f(x) 
, заданной на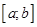 
, вычисляется с помощью интеграла
D)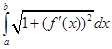 
120.1. Объем тела, полученного от вращения вокруг оси OX криволинейной трапеции, вычисляется с помощью интеграла
E) 
121.1. Длина кривой y=f(x), 
, вычисляется с помощью интеграла
A)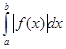 
122.1. Площадь области, ограниченной прямыми x=a, x=b (a<b),y=c и кривой y=f(x), где 
вычисляется по формуле
C) S= 
123.1. Найти площадь фигуры, ограниченной линиями y=-x2 , у+x+2=0
С) 
124.1. Вычислить объем тела, полученного от вращения вокруг оси OX фигуры, ограниченной прямыми y=x, x=3 и осью OX
B) 
125.1.Площадь области, ограниченной прямыми x=a, x=b (a<b) и кривыми y=f(x) – сверху и y=g(x) – снизу равна:
A) 
126.1. Если v(t) – скорость движения материальной точки по некоторой прямой, тогда путь s, пройденный этой точкой за промежуток времени [t1, t2]определяется по формуле:
A) 
127.1. Алгебраическая форма записи комплексного числа z имеет вид:
E) z =а + bi
128.1. Указать тригонометрическую форму комплексного числа:
В) 
129.1. Указать показательную форму комплексного числа:
С)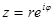 
130.1. Два комплексных числа называются сопряженными, если
