МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФИЛИАЛ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Московский технологический университет» в г. Ставрополе
Филиал МИРЭА в г. Ставрополе
Кафедра «автоматизированные системы управления»
Специальность 09.03.01 «Информатика и вычислительная техника»
КУРСОВАЯ РАБОТА
по дисциплине:
«Математическая логика и теория алгоритмов»
На тему: Логика высказываний и элементы теории алгоритмов
Вариант № 5
Выполнил:
Студент группы СВБО-01-15 ______________ Зыков Д.С.
(подпись)
Проверил:
Доцент, к.т.н. _______________ Авакян Т.А.
(подпись)
г. Ставрополь 2016г.
Содержание
1 Алгебра логики высказываний. 3
2 Построение таблицы истинности. 4
3 Дизъюктивная нормальная форма. 6
4 Конъюктивная нормальная форма. 7
5 Машина Тьюринга. 8
Список используемой литературы.. 10
Введение
АЛГЕБРА ЛОГИКИ ВЫСКАЗЫВАНИЙ
Алгебра логики (алгебра высказываний) – раздел математической логики, в котором изучаются логические операции над высказываниями. Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика, в отличие от, например, троичной логики.
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.
Высказывание - это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным или ложным.
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух), связанных логическими операциями.
Логические операции – операции, выполняемые в соответствии с правилами булевой алгебры. К ним относят операции: отрицания, логическое «и», логическое «или» и тождество (эквивалентность). На этих логических операциях основана работа вычислительных машин. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Своим существованием наука «алгебра логики» обязана английскому математику Джорджу Булю, который исследовал логику высказываний.
Задание 1 Определите, истинно или ложно последнее высказывание, исходя из истинности или ложности предыдущих высказываний.
 ,
,  ,
,  ;
;
Решение задачи
| a | b | a | b | a˄b | a˅b | (a→b)˅a | (a→b)˅a | (a˄b)˅a)˄(a˅b)˅a |
Ответ: исходя из условия эквивалентности, данное высказывание будет ложным.
Построение таблицы истинности
Таблица истинности – это такая таблица, в которой отражены все значения логической функции при всех возможных значениях, входящих в неё логически.
Алгоритм составления таблицы истинности:
1. Подсчитать количество переменных n.
2. Подсчитать количество строк m=2^n.
3. Количество столбцов = n+ количество логических операций.
Основные логические функции
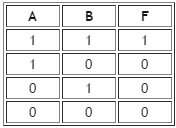
Рисунок 2.1 – Конъюнкция

Рисунок 2.2- Дизъюнкция
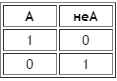
Рисунок 2.3 – Инверсия

Рисунок 2.4 – Импликация

Рисунок 2.5 – Эквивалентность
Задание 2 Составьте таблицу истинности для формулы алгебры высказываний.
X ↔ ((Y ˅ Z) → (X ˅ Y))
Решение задачи
11) X↔((Y˅Z)→(X˅Y))
12) (X)↔((Y˅Z)→(X˅Y))
| X | Y | Z | X | Z | Y˅Z | Y | X˅Y | (X˅Y) | (Y˅Z)→(X˅Y) | ||






