В качестве временной нагрузки при расчете плиты проезжей части принимается тележка нагрузки А14 с давлением на ось 140 кН (на колесо 70 кН), а также нагрузка Н14 с давлением на ось 252 кН (на колесо 126кН)
| Наименование слоя | Толщина слоя hi (м) | Объёмный вес материала yi (Н) | Нормативный вес hi yi | Коэффициент надёжности по нагрузке yf | Расчетный вес hi yi yf |
| Выравнивающий слой | 0.1 | 1.3 | |||
| Гидроизоляция | 0.02 | 1.3 | |||
| Защитный слой | 0.04 | 1.3 | |||
| Покрытие а/б | 0.05 | 1.5 | |||
| Всего от дорожной одежды | |||||
| Вес ЖБ плиты | 0.18 | 1.1 | |||
| Суммарная постоянная нагрузки |
Перед определением усилий в плите необходим расчет параметров диаграммы, показывающей, какая часть плиты в перпендикулярном направлении воспринимает временную нагрузку. Вид диаграммы представлен на рисунке 1, а расчет ее параметров в таблице 1.
Таблица 1. Параметры диаграммы распределения временной нагрузки
| Вид временной нагрузки | a, м |  м
м
|  , но не менее , но не менее 
|  но не менее но не менее 
|  , м , м
|  м м
| 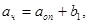 но не более но не более 
|
| А14 | 0,2 | 0,44 | 0,51 | 1,02 | 0,6 | 1,02 | 1,02 |
| Н14 | 0,2 | 0,44 | 0,51 | 1,02 | 0,8 | 1,22 | 1,02 |
Изгибающий момент в середине пролета расчетной схемы от действия колес АК или НК для расчетов по первой группе предельных состояний определяется по формуле:
 ,
,
где Рк – давление колеса, равное для одного колеса нагрузки А14 70кН, для Н14 126кН; γf – коэффициент надежности по нагрузке, принимаемый по п.2.22[1]. Для тележки А14 при расчетах элементов проезжей части γf =1,5 и для Н14 γf =1,0; (1+μ) – динамический коэффициент, находится по п.2.22[1] в зависимости от длинны загружения λ для А14 находится по формуле:
 , но не менее 1,0;
, но не менее 1,0;
для Н14 (1+μ) =1,0 при  м.
м.
Для нагрузки А14:

Для нагрузки Н14:

Находим ординату у на линии влияния под силой Рк по формуле:


Для нагрузки А14:
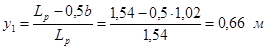

Для нагрузки Н14:

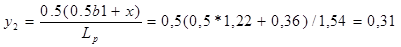
Поперечная сила находится по формуле:

где ах – рабочая ширина плиты под нагрузкой
Для нагрузки А14: 
Для нагрузки Н14:

Выбор расчетных усилий и учет неразрезности конструкции
Неразрезность плиты учитывается вводом коэффициента η принимаемый в зависимости от положения нагрузки и отношения толщины плиты к высоте балки:

тогда: η пр=+0,5, η оп=-0,7
η пр=-0,25, η оп=+0,25
Подсчет усилий й выбор их значений к дальнейшему расчету может быть произведен в форме таблицы
Таблица 3 – Выбор усилий в сечениях плиты
| Вид нагрузки | Изгибающий момент в разрезной схеме, кН*м | Отношение hпл/hб | Усилия в плите с учетом ее неразрезности | ||||||
| Для расчета по первой группе предельных состояний, т·м | Для расчета по второй группе предельных состояний, т·м | ||||||||
| Мо | Мон | η пр | η оп | Мпр | Моп | Qоп | Мпрн | Мопн | |
| А14 | 38,31 | 19,31 | +0,5 | -0,7 | 19,15 | -26,81 | 66,05 | 9,65 | -13,51 |
| Н14 | 32,44 | 32,44 | +0,5 | -0,7 | 16,22 | -22,70 | 94,79 | 16,22 | -22,70 |
Нормативный изгибающий момент находится по формуле:

Определение усилий от участия плиты в общей работе пролётного строения.
Кроме локального воздействия колёс временной нагрузки плита, являясь частью единой частью пространственной системы пролётного строения воспринимает поперечные изгибающие моменты, возникающие из-за различия величин прогибов главных балок в сечениях, тяготеющий к средней части пролёта.
Добавочный момент вычисляется по формуле:
Мпл.о.= Впл. / p
, где Впл=0,8ЕbJпл и p=(c2+∆2yi)/2∆yi, где ∆yi=yi-((∆yi-1+∆yi+1)/2)




