1.5. ƒосл≥дженн€ потреби шифруванн€ на п≥дприЇмств≥
¬з€вши за основу Ќ¬ѕѕ Ђ≈нерготехснабї, ви€вилос€, що нав≥ть п≥дприЇмство, €ке займаЇтьс€ торг≥влею i знаходитьс€ на в≥дстан≥ в≥д IT-технолог≥й, потребуЇ захисту ≥нформац≥њ. ќдин з шл€х≥в вир≥шенн€ цього питанн€ i Ї шифруванн€.
як i будь-€ке ≥нше п≥дприЇмство, Ђ≈нерготехснабї веде бухгалтерський обл≥к, дл€ зручност≥ використовуЇтьс€ платформа Ђ1—ї. ƒл€ безпеки баз даних, до €ких не вс≥ люди повинн≥ мати доступ, i потр≥бен над≥йний алгоритм шифруванн€.
«вичайно, що це не допоможе зб≥льшити прибуток п≥дприЇмства, але y випадку атаки на хакер≥в, ≥нформац≥ю можуть використати в своњх ц≥л€х ≥, таким чином, зароб≥ток може знизитис€. “ому захист даних за допомогою криптограф≥чноњ системи необх≥дний б≥льшост≥ п≥дприЇмств i Ђ≈нерготехснабї не виключенн€.
1.6. Ќайпоширен≥ш≥ методи шифруванн€
Ўифр ÷езар€:
Ўифр ÷езар€ Ч симетричний алгоритм шифруванн€ п≥дстановками. ¬икористовувавс€ римським ≥мператором ёл≥Їм ÷езарем дл€ приватного листуванн€.
ѕринцип д≥њ пол€гаЇ в тому, щоб цикл≥чно зсунути алфав≥т, а ключ Ч це к≥льк≥сть л≥тер, на €к≥ робитьс€ зсув.
якщо з≥ставити кожному символу алфав≥ту його пор€дковий номер (нумеруючи з 0), то шифруванн€ ≥ дешифруванн€ можна виразити формулами:
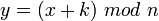 (1.1)
(1.1)
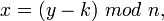
де 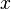 Ч символ в≥дкритого тексту,
Ч символ в≥дкритого тексту, 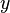 Ч символ шифрованого тексту,
Ч символ шифрованого тексту, 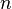 Ч потужн≥сть алфав≥ту, а
Ч потужн≥сть алфав≥ту, а 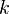 Ч ключ.
Ч ключ.
ћожна пом≥тити, що суперпозиц≥€ двох шифрувань на ключах 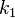 ≥
≥ 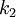 Ї просто шифруванн€м на ключ≥
Ї просто шифруванн€м на ключ≥  . Ѕ≥льш загально, множина шифруючих перетворень шифру ÷езар€ утворюЇ групу
. Ѕ≥льш загально, множина шифруючих перетворень шифру ÷езар€ утворюЇ групу 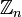 .
.
Ўифр ÷езар€ маЇ замало ключ≥в Ч на одиницю менше, н≥ж л≥тер в абетц≥. “ому перебрати ус≥ ключ≥ не складаЇ особливоњ роботи. ƒешифруванн€ з одним з ключ≥в дасть нам в≥рний в≥дкритий текст.
“акож зламати шифр ÷езар€ також можна, €к ≥ звичайний п≥дстановочний шифр, у звТ€зку з тим, що частота по€ви кожноњ л≥тери в шифртекст≥ зб≥гаЇтьс€ з частотою по€ви у в≥дкритому текст≥. якщо припустити, що частота по€ви л≥тер у в≥дкритому текст≥ приблизно в≥дпов≥даЇ середньостатистичн≥й в≥дносн≥й частот≥ по€ви л≥тер в текстах мови, на €к≥й написано пов≥домленн€, тод≥ ключ знаходитьс€ з≥ставленн€м перших дек≥лькох л≥тер, що трапл€ютьс€ найчаст≥ше у в≥дкритому та зашифрованому текстах. “обто за допомогою методу частотного криптоанал≥зу. [5]
Ўифр ¬≥женера:
ѕол≥алфав≥тний шифр, €кий у €кост≥ ключа використовуЇ слово. лючове слово повторюЇтьс€, поки не отримано гаму, р≥вну довжин≥ пов≥домленн€.
ќтримав назву на честь Ѕлеза де ¬≥женера. Ci = (Pi + Kj) mod 33 (P≥, Kj, Ci Ц м≥сце в алфав≥т≥ виражене через цифри). —≥ Ц буква, €ку потр≥бно зашифрувати, –≥ Ц буква по верхньому р€ду, ≥ Ц буква по нижньому р€ду таблиц≥.
“аблиц€ 1.1
“аблиц€ дл€ кодуванн€ по шифру ¬≥женера
| _ | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € |
| а | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € |
| б | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а |
| в | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б |
| г | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в |
| і | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г |
| д | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і |
| е | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д |
| Ї | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е |
| ж | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї |
| з | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж |
| и | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з |
| ≥ | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и |
| њ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ |
| й | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ |
| к | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й |
| л | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к |
| м | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л |
| н | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м |
| о | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н |
| п | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о |
| р | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п |
| с | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р |
| т | т | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с |
| у | у | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т |
| ф | ф | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у |
| х | х | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф |
| ц | ц | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х |
| ч | ч | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц |
| ш | ш | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч |
| щ | щ | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш |
| ь | ь | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ |
| ю | ю | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь |
| € | € | а | б | в | г | і | д | е | Ї | ж | з | и | ≥ | њ | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю |
ѕо вертикал≥ вибираЇмо л≥тери в≥дкритого тексту, а по горизонтал≥ Ч ключа, на перетин≥ цих значень отримуЇмо знаки шифротексту. Ќаприклад:
¬≥дкритий текст: Ђпол≥/алфа/в≥тн/ий ши/фрї
люч: Ђключ/ключ/ключ/кл юч/клї
Ўифротекст: Ђаайд/кьтч/мцр≥/фш ці/двї. [6]
Ўифр ¬ермана:
у криптограф≥њ ц€ система шифруванн€ винайдена в 1917 роц≥ сп≥вроб≥тниками AT&T ƒжозефом ћоборном ≥ √≥льбертом ¬ернамом.
ƒл€ в≥дтворенн€ шифртексту в≥дкритий текст об'ЇднуЇтьс€ операц≥Їю Ђвиключне јЅќї з ключем (названим одноразовим блокнотом або шифроблокнотом). ѕри цьому ключ повинен волод≥ти трьома критично важливими властивост€ми:
1. Ѕути справд≥ випадковим;
2. «б≥гатис€ з розм≥ром з заданим в≥дкритим текстом;
3. «астосовуватис€ т≥льки один раз.
Ўифр названий на честь телеграф≥ста AT&T √≥льберта ¬ернама, що в 1917 роц≥ побудував телеграфний апарат, €кий виконував цю операц≥ю автоматично - треба було т≥льки подати на нього стр≥чку з ключем. Ќе будучи шифрувальником, тим не менше, ¬ернам в≥рно пом≥тив важливу властив≥сть свого шифру - кожна стр≥чка повинна використовуватис€ т≥льки один раз ≥ п≥сл€ цього знищуватис€.
¬ 1949 роц≥ лод Ўеннон опубл≥кував роботу, в €к≥й дов≥в абсолютну ст≥йк≥сть шифру ¬ернама. ≤нших шифр≥в з ц≥Їю властив≥стю не ≥снуЇ. ÷е по сут≥ означаЇ, що шифр ¬ернама Ї найбезпечн≥шою криптосистемою з ус≥х можливих. ѕри цьому умови, €ким повинен задовольн€ти ключ, наст≥льки сильн≥, що практичне використанн€ шифру ¬ернама Ї важко зд≥йсненним. “ому в≥н використовуЇтьс€ т≥льки дл€ передач≥ пов≥домлень найвищоњ секретност≥.
Ќа початку 20 ст. дл€ передач≥ пов≥домлень все ширше ≥ ширше використовувалис€ телетайпи. “ому потр≥бн≥ були методи, що дозвол€ють шифрувати текст не до того, €к в≥н потрапл€Ї до телеграф≥ста, а безпосередньо в момент передач≥, ≥, в≥дпов≥дно, розшифровувати в момент прийому.
ѕодальше вдосконаленн€ методу, запропонованого ¬ернамом, належить майбутньому начальнику зв'€зку в≥йськ —Ўј ƒжозеф ћоборну, що об'Їднав хаотичн≥сть Ђгамиї, на €ку спиравс€ ¬ернам у своњй систем≥ Ђавтоматичного шифруванн€ї, з використовуваним у той час у в≥йськах правилом Ђодноразового шифрблокнотаї. ≤де€ ћоборна пол€гала в тому, що кожна випадкова Ђгамаї повинна використовуватис€ один, ≥ т≥льки один раз. ѕри цьому дл€ шифруванн€ кожного знака вс≥х текст≥в, €к≥ вже передан≥ або будуть передан≥ в найближчому майбутньому, повинен застосовуватис€ абсолютно новий ≥ такий, що не п≥ддаЇтьс€ передбаченню знак Ђгамиї.
Ќа практиц≥ можна один раз ф≥зично передати нос≥й ≥нформац≥њ з довгим д≥йсно випадковим ключем, а пот≥м по м≥р≥ необх≥дност≥ пересилати пов≥домленн€. Ќа цьому заснована ≥де€ шифроблокнот≥в: шифрувальник при особист≥й зустр≥ч≥ забезпечуЇтьс€ блокнотом, кожна стор≥нка €кого м≥стить ключ. “акий же блокнот Ї ≥ у приймаючоњ сторони. ¬икористан≥ стор≥нки знищуютьс€.
р≥м того, €кщо Ї два незалежних канали, в кожному з €ких ймов≥рн≥сть перехопленн€ низька, але в≥др≥зн€Їтьс€ в≥д нул€, шифр ¬ернама також можна застосувати: по одному каналу можна передати зашифроване пов≥домленн€, по другому - ключ. ƒл€ того, щоб розшифрувати пов≥домленн€, перехоплювач повинен прослуховувати обидва канали.
Ўифр ¬ернама може застосовуватис€, €кщо Ї односторонн≥й захищений канал: ключ передаЇтьс€ в одну сторону п≥д захистом каналу, пов≥домленн€ в ≥ншу сторону захищаютьс€ ключем.
” пер≥од м≥ж двома св≥товими в≥йнами в б≥льшост≥ крањн з'€вл€ютьс€ електромехан≥чн≥ шифратори. ¬они були двох тип≥в. ѕерший - пристр≥й, що складаЇтьс€ з комутац≥йних диск≥в та механ≥зму зм≥ни њх кутових положень. «а обома сторонами комутац≥йного диска розм≥щен≥ контакти, в≥дпов≥дн≥ алфав≥ту в≥дкритого та шифрованого тексту. онтакти ц≥ з'Їднуютьс€ м≥ж собою в≥дпов≥дно до де€кого правила п≥дстановки, що зветьс€ комутац≥Їю диска. ÷€ комутац≥€ визначаЇ зам≥ну л≥тер в початковому кутовому положенн≥. ѕри зм≥н≥ кутового положенн€ диска зм≥нюЇтьс€ ≥ правило п≥дстановки. “аким чином, ключ шифруванн€ м≥стить к≥лька нев≥домих: схему з'Їднанн€ контакт≥в ≥ початкове кутове положенн€. якщо п≥сл€ шифруванн€ кожноњ л≥тери м≥н€ти кутове положенн€ диска - отримаЇмо багато алфав≥тне шифруванн€. ўе б≥льш складний пристр≥й отримаЇмо, з'Їднавши посл≥довно к≥лька диск≥в, кутов≥ положенн€ €ких зм≥нюютьс€ з р≥зною швидк≥стю.
Ўироко в≥дома шифрмашина Ђ≈н≥гмаї, €кою були оснащен≥ н≥мецьк≥ в≥йська час≥в ƒругоњ св≥товоњ в≥йни, Ї типовим прикладом пристрою на комутац≥йних дисках. онструктивно Ђ≈н≥гмаї походила на звичайну друкарську машинку, т≥льки натисканн€ клав≥ш≥ призводило не до удару молоточка по паперу, а створювало електричний ≥мпульс, що надходив у схему криптоперетворенн€. јмериканська шифрмашина ћ-209 - типовий приклад другого типу шифратора.
“аким чином, перед ƒругою св≥товою в≥йною вс≥ пров≥дн≥ крањни мали на озброЇнн≥ електромехан≥чн≥ шифрсистеми, що волод≥ють високою швидк≥стю обробки ≥нформац≥њ ≥ високою ст≥йк≥стю. ¬важалос€, що застосовуван≥ системи неможливо розшифрувати ≥ криптоанал≥зу б≥льше робити абсолютно н≥чого. як часто буваЇ, ц€ думка була згодом спростована, ≥ дешифровщики були безпосередн≥ми учасниками бойових д≥й.
«авд€ки накладеним обмеженн€м на ключ, в 1949 роц≥ лод Ўенон дов≥в, що шифр ¬ернама Ї абсолютно криптост≥йким. јле:
1. ƒл€ роботи шифру ¬ернама необх≥дна д≥йсно випадкова посл≥довн≥сть нул≥в та одиниць (ключ). «а визначенн€м, посл≥довн≥сть, отримана з використанн€м будь-€кого алгоритму, Ї не зовс≥м випадковою, а псевдовипадковою. “обто, потр≥бно отримати випадкову посл≥довн≥сть неалгор≥тм≥чно (наприклад, використовуючи рад≥оактивний розпад €дер, створений електронним генератором б≥лий шум або ≥нш≥ досить випадков≥ под≥њ).
2. ѕроблемою Ї таЇмна передача посл≥довност≥ та збереженн€ њњ в таЇмниц≥. якщо ≥снуЇ над≥йно захищений в≥д перехопленн€ канал передач≥ пов≥домлень, шифри взагал≥ не потр≥бн≥: секретн≥ пов≥домленн€ можна передавати з цього каналу. ѕри цьому, оск≥льки довжина ключа така ж, €к ≥ довжина пов≥домленн€, передати його не прост≥ше, н≥ж пов≥домленн€. Ўифроблокнот на ф≥зичному нос≥њ можна вкрасти або скоп≥ювати.
3. ћожлив≥ проблеми з над≥йним знищенн€м використаноњ стор≥нки. ÷ьому схильн≥ €к паперов≥ стор≥нки блокнота, так ≥ сучасн≥ електронн≥ реал≥зац≥њ з використанн€м компакт-диск≥в або флеш-пам'€т≥.
4. якщо трет€ сторона €кимось чином д≥знаЇтьс€ пов≥домленн€, вона легко в≥дновить ключ ≥ зможе п≥дм≥нити пов≥домленн€ на ≥нше такоњ ж довжини.
5. Ўифр ¬ернама чутливий до будь-€кого порушенн€ процедури шифруванн€. Ќаприклад, контррозв≥дка —Ўј часто розшифровувала рад€нськ≥ та н≥мецьк≥ посланн€ через неточност≥ генератора випадкових чисел. Ѕували випадки, коли одна ≥ та ж стор≥нка блокнота застосовувалас€ дв≥ч≥ - —Ўј також розшифровували так≥ посланн€. [7]
|
|
|
|
|
|
|
|
|
Ќаприклад:
—лово "ћоскаленко" ключ 57065
1 листок: 38902...
2 листок: 57065 23252 82110 22152 42125
3 листок: 23056...
“екст "привет мир" ключ 57065
1 листок: 28763...
2 листок: 73521...
3 листок: 57065 26271 91215 29432 31927
одуванн€ алфав≥ту виконуватиметьс€ в так≥й посл≥довност≥: 0 Ц 00Е, 9 Ц 09Е, а Ц 10Е, € Ц 43.
RSA:
RSAЧ криптограф≥чна система з в≥дкритим ключем.
RSA став першим алгоритмом такого типу, придатним ≥ дл€ шифруванн€ ≥ дл€ цифрового п≥дпису. јлгоритм використовуЇтьс€ у велик≥й к≥лькост≥ криптограф≥чних застосунк≥в.
ќпис алгоритму:
Ѕезпека алгоритму RSA побудована на принцип≥ складност≥ факторизац≥њ ц≥лих чисел. јлгоритм використовуЇ два ключ≥ Ч в≥дкритий (public) ≥ секретний (private), разом в≥дкритий ≥ в≥дпов≥дний йому секретний ключ≥ утворюють пари ключ≥в (keypair). ¬≥дкритий ключ не потр≥бно збер≥гати в таЇмниц≥, в≥н використовуЇтьс€ дл€ шифруванн€ даних. якщо пов≥домленн€ було зашифровано в≥дкритим ключем, то розшифрувати його можна т≥льки в≥дпов≥дним секретним ключем.
ƒл€ того, щоб згенерувати пари ключ≥в виконуютьс€ так≥ д≥њ:
вибираютьс€ два велик≥ прост≥ числа 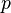 ≥
≥ 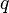 приблизно 512 б≥т завдовжки кожне;
приблизно 512 б≥т завдовжки кожне;
обчислюЇтьс€ њх добуток  ; (1.2)
; (1.2)
обчислюЇтьс€ функц≥€ ≈йлера 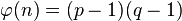 ; (1.3)
; (1.3)
вибираЇтьс€ ц≥ле  таке, що
таке, що 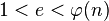 та
та  взаЇмно просте з
взаЇмно просте з 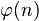 ;
;
за допомогою розширеного алгоритму ≈вкл≥да знаходитьс€ число 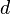 таке, що
таке, що 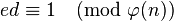 ; (1.4)
; (1.4)
„исло 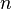 називаЇтьс€ модулем, а числа
називаЇтьс€ модулем, а числа  ≥
≥ 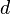 Ч в≥дкритою й секретною експонентами в≥дпов≥дно. ѕари чисел
Ч в≥дкритою й секретною експонентами в≥дпов≥дно. ѕари чисел 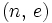 Ї в≥дкритою частиною ключа, а
Ї в≥дкритою частиною ключа, а 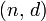 Ч секретною. „исла
Ч секретною. „исла 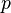 ≥
≥ 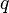 п≥сл€ генерац≥њ пари ключ≥в можуть бути знищен≥, але в жодному раз≥ не повинн≥ бути розкрит≥.
п≥сл€ генерац≥њ пари ключ≥в можуть бути знищен≥, але в жодному раз≥ не повинн≥ бути розкрит≥.
ƒл€ того, щоб зашифрувати пов≥домленн€ 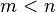 обчислюЇтьс€
обчислюЇтьс€
|
|
|






