Численные методы расчета строительных конструкций
Экзаменационная программа и контрольные задания
для студентов очной и заочной формы обучения по направлению подготовки «Строительство»
Нижневартовск- 2016г.
Методические указания по курсу «Численные методы расчета строительных конструкций» для студентов инженерных специальностей /Сост.: З.К. Нураева, – Нижневартовск, 2016. – 13 с.
Предлагаемые методические указания имеют целью помочь студентам инженерных специальностей освоить курс «Численные методы расчета строительных конструкций» и выполнить предусмотренные учебным планам типовые задачи.
Методические указания содержат:
- Введение.
- Общие методические указания к выполнению типовых заданий.
- Типовые задания - 10 вариантов
- Литература
Правила выполнения и оформления контрольных работ
- При оформлении контрольных работ необходимо придерживаться указанных ниже правил.
- Номер варианта выбирается по двум последним цифрам шифра студента.
| Номер варианта | |||||||||||
| Две последние цифры | |||||||||||
- Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 4-5 см для замечаний рецензента.
- На обложке тетради должны быть ясно написаны фамилия студента, его инициалы учебный номер (шифр), название дисциплины, номер контрольной работы, здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента. В конце работы следует поставить дату её выполнения и подпись студента.
- В работу должны быть включены все задачи, указанные в задании, строго по полагающемуся варианту.
- Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номер задач.
- Перед решением каждой задачи надо полностью выписать её условие. Решения задач следует излагать подробно и аккуратно, объясняя все действия по ходу решения и делая необходимые чертежи.
- Работа сдается на проверку не позже двух недель до начала сессии.
- После получения прорецензированной незачтенной работы студент должен исправить все отмеченные рецензентом ошибки и недочёты и прислать работу ещё раз.
- Зачтенные контрольные работы предъявляются студентом при сдаче экзамена или зачета.
Вопросы к зачету по дисциплине «Численные методы расчета строительных конструкций»
1. Источники погрешностей. Понятие приближенного числа. Абсолютная и относительная погрешности. Верные цифры числа. Связь относительной погрешности с количеством верных знаков числа. Погрешность суммы, разности, произведения, частного, степени. Общая формула для погрешности функции. Обратная задача теории
2. Постановка вычислительной задачи, обусловленность вычислительной задачи, корректность вычислительных алгоритмов, требования, предъявляемые к вычислительным алгоритмам.
3. Метод половинного деления. Метод хорд.
4. Метод Ньютона. Метод секущих.
5. Численной решение уравнений с одной переменной. Метод последовательных приближений (метод итераций). Достаточные условия сходимости метода итераций.
6. Функции в Mathcad для решения одного уравнения. В каких случаях Mathcad не может найти корень уравнения?
7. Итерационные методы решения СЛАУ: метод простой итерации, метод Зейделя. Сходимость итерационных процессов. Погрешности итерационных процессов.
8. Решение переопределенной СЛАУ методом наименьших квадратов.
9. Нормы матриц и методы их вычислений. Вычисление норм в Mathcad.
10. Метод Зейделя и его особенности. Решение систем нелинейных уравнений в системе Mathcad.
11. Интерполирование функций. Интерполяционный многочлен Лагранжа. Погрешность интерполяции. Минимизация погрешности.
12. Интерполяционный многочлен Ньютона. Погрешность интерполяции.
13. Численное интегрирование. Метод прямоугольников, метод трапеций. Погрешность вычислений.
14. Преобразование Фурье, дискретное преобразование.
15. Тригонометрическая интерполяция. Приближение сплайнами. Линейные, параболические, кубические сплайны.
16. Ортогональные системы функций (показательные и тригонометрические функции).
17. Общий способ получения формул численного дифференцирования. Погрешности дифференцирования. Обусловленность формул численного дифференцирования.
18. Численное дифференцирование. Простейшие формулы численного дифференцирования:
Вычисление первой производной, вычисление второй производной.
19. Погрешность квадратурных формул. Обусловленность квадратурных формул. Правило Рунге оценки погрешности квадратурных формул.
20. Численные методы решения обыкновенных дифференциальных уравнений Постановка задачи. Устойчивость решения задачи Коши: устойчивость на конечном отрезке, устойчивость по правой части.
21. Численные методы решения задачи Коши (сетки и сеточные функции), дискретная задача Коши, явные и неявные методы, устойчивость).
22. Численные методы решения обыкновенных дифференциальных уравнений. Интегрирование дифференциальных уравнений с помощью степенных рядов.
23. Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера.
24. Численные методы решения обыкновенных дифференциальных уравнений. Метод Рунге-Кутта, схемы 1, 2, 3 и 4 порядков точности.
25. Однородные системы линейных уравнений и методы их решения в систему MathCAD.
26. Метод наименьщих квадратов. Решение задачи, предложенной преподавателем, методом наименьших квадратов при помощи MathCAD.
27. Собственные числа и собственные векторы матрицы. Решение задачи, предложенной преподавателем, при помощи MathCAD. Решение переопределенной СЛАУ методом наименьших квадратов.
28. Преобразование Фурье, дискретное преобразование. Решение задачи, предложенной преподавателем, при помощи MathCAD.
29. Численное интегрирование функций. Программирование метода трапеций, прямоугольников при помощи MathCAD. Решение задачи, предложенной преподавателем, при помощи MathCAD.
30. Численные методы решения задачи Коши: Метод Эйлера. Реализация метода в системе Mathcad.
31. Численные методы решения задачи Коши: Метод Рунге-Кутта. Реализация метода в системе Mathcad.
32. Интегрирование дифференциальных уравнений с помощью степенных рядов. Реализация метода в системе Mathcad.
33. Численные методы решения задачи Коши: Метод Пикара. Реализация метода в системе Mathcad.
34. Функции Mathcad, реализующие приближенные вычисления при помощи рядов.
Метод половинного деления
Метод половинного является самым простым и надежным способом решения нелинейного уравнения. Пусть из предварительного анализа известно, что корень уравнения находится на отрезке  , т. е.
, т. е.  , так, что
, так, что  . Пусть функция
. Пусть функция  непрерывна на отрезке
непрерывна на отрезке  и принимает на концах отрезка значения разных знаков, т.е.
и принимает на концах отрезка значения разных знаков, т.е.  .
.
Разделим отрезок  пополам. Получим точку
пополам. Получим точку 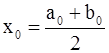 . Вычислим значение функции в этой точке:
. Вычислим значение функции в этой точке:  . Если
. Если  , то
, то  - искомый корень, и задача решена. Если
- искомый корень, и задача решена. Если  , то
, то  - число определённого знака:
- число определённого знака: 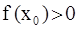 , либо
, либо  . Тогда либо на концах отрезка
. Тогда либо на концах отрезка  , либо на концах отрезка
, либо на концах отрезка  значения функции
значения функции  имеют разные знаки. Обозначим такой отрезок
имеют разные знаки. Обозначим такой отрезок  . Очевидно, что
. Очевидно, что  , и длина отрезка
, и длина отрезка  в два раза меньше, чем длина отрезка
в два раза меньше, чем длина отрезка  . Поступим аналогично с отрезком
. Поступим аналогично с отрезком  . В результате получим либо корень
. В результате получим либо корень 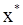 , либо новый отрезок
, либо новый отрезок 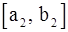 и т.д.
и т.д.
Середина  -го отрезка
-го отрезка  . Очевидно, что длина отрезка
. Очевидно, что длина отрезка  будет равна
будет равна  , а так как
, а так как 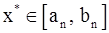 , то
, то
 . (1)
. (1)
Критерий окончания. Из соотношения (1) следует, что при заданной точности приближения  вычисления заканчиваются, когда будет выполнено неравенство
вычисления заканчиваются, когда будет выполнено неравенство  или неравенство
или неравенство  . Таким образом, количество итераций можно определить заранее. За приближенное значение корня берется величина
. Таким образом, количество итераций можно определить заранее. За приближенное значение корня берется величина  .
.






