БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра "Конструирование и производство приборов"
АВТОМАТИКА
Программа, методические указания и задания
по дисциплине «Автоматика» для студентов заочного отделения специальности 1-38 01 01 «Механические и электромеханические приборы и аппараты»
М и н с к 2015
Введение
В настоящее время во всех областях техники имеется тенденция к автоматизации различных процессов. В производственные процессы широко внедряются современные системы управления, в том числе на основе микропроцессорной техники. В таких условиях также растет актуальность технических средств, позволяющих управлять объектами на значительном расстоянии, концентрировать системы управления большим количеством объектов из одного центра или диспетчерского пункта. В связи с этим является актуальной подготовка инженеров, владеющих вопросами проектирования систем автоматического управления, регулирования и устройств телемеханики.
В настоящем курсе изложены вопросы построения, анализа и синтеза перечисленных систем, являющиеся теоретической и практической основой их расчета и проектирования.
ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ
Целью изучения дисциплины является формирование базовых знаний в области проектирования систем автоматического управления (САУ) и регулирования (САР). Основными задачами дисциплины являются изучение принципов построения, математических методов анализа и синтеза и элементной базы САУ и САР.
Дисциплина «Автоматика» базируется на физико-математической и электромеханической подготовке студентов, обеспечиваемой курсами «Математика», «Физика», «Теоретические основы электротехники», «Электроника», «Теоретическая механика» и другими. В основе дисциплины лежат фундаментальные положения математики, механики, электротехники и электроники.
Знания и умения, полученные студентами при изучении данной дисциплины, необходимы для освоения последующих специальных дисциплин и дисциплин специализаций, связанных с проектированием и расчетом автоматических систем управления и регулирования в различных областях приборостроения, а также анализом динамических свойств приборов и технологических агрегатов, таких как:
«Автоматизация производственных процессов в приборостроении», «Системы управления техническими объектами» (специальность 1-38 01 01);
В результате освоения дисциплины «Автоматика» студент должен:
знать:
– алгоритмы автоматического регулирования и основные технические средства автоматики;
– основные принципы и концепции построения систем автоматического управления;
– описание динамических систем и звеньев автоматики;
– элементы систем автоматического регулирования и управления;
– принципы анализа и синтеза систем автоматического управления и регулирования;
– методы управления выходными параметрами замкнутых систем;
уметь:
– выбрать и обосновать функциональную схему автоматической системы управления и регулирования;
– выбрать структуру и схему регулирования и управления физическими величинами;
– определять передаточные функции динамических звеньев и находить математическую модель системы в целом;
– определять АФЧХ замкнутых систем;
– производить исследование устойчивости, оценку качества и синтез линейных непрерывных и дискретных систем автоматического регулирования;
– производить синтез корректирующих устройств последовательного, параллельного и встречно- параллельного действия, с целью улучшения качества процесса управления;
– применять типовые автоматические устройства в производственных процессах;
– регулировать качество процесса управления.
НАИМЕНОВАНИЕ ТЕМ, ИХ СОДЕРЖАНИЕ
1. Введение
Роль автоматики в машино- и приборостроении. Краткий исторический очерк развития автоматики.
Литература: [1, c. 3, 8 – 10], [2, c. 9 –12]
2. Общие сведения об автоматических системах управления и регулирования
Общие понятия об управлении и регулировании. Основные понятия и определения. Фундаментальные принципы построения систем автоматического управления (САУ). Принцип разомкнутого управления. Принцип управления по возмущению (принцип компенсации). Принцип обратной связи. Разомкнутые и замкнутые САУ. Классификация САУ. Общие принципы классификации. Стабилизирующие и программные САР. Следящие САР. Статические и астатические САР.
Литература: [1, c. 6 – 29, 32 – 73], [5, c. 18 – 31]
3. Математические модели линейных САУ
Математическая модель связей входа и выхода составных частей материальных систем. Описание связей в технических системах с помощью дифференциальных уравнений. Линеаризация дифференциальных уравнений в автоматике. Основные формы записи линейных дифференциальных уравнений в автоматике. Уравнения статики. Статические характеристики элементов САУ. Вывод уравнений элементов САУ.
Литература: [1, c. 89 – 122], [5, c. 56 – 88]
4. Динамические характеристики звеньев и САУ
Типовые воздействия и реакция на них линейных объектов. Передаточная функция. Связь передаточной функции с дифференциальным уравнением. Переходная и импульсная переходная функции, связь их с передаточной функцией. Постоянная времени динамического звена. Составление дифференциальных уравнений САУ. Исследование САУ по дифференциальным уравнениям в установившемся режиме. Частотные характеристики и частотные передаточные функции. Связь частотных характеристик с дифференциальными уравнениями. Логарифмические частотные характеристики. Типовые динамические звенья и их характеристики. Позиционные звенья: безынерционное, апериодические 1-го и 2-го порядков, колебательное, консервативное. Дифференцирующие звенья: идеальное, реальное. Интегрирующие звенья: идеальное, реальное. Звенья с запаздыванием.
Литература: [1, c. 93 – 149], [5, c. 61 – 113]
5. Структурные схемы САУ
Составление структурных схем САУ. Элементы структурных схем: динамическое звено, сравнивающее устройство, сумматор, узел. Типовые соединения звеньев: последовательное, параллельное, встречно-параллельное. Основные и дополнительные правила преобразования структурных схем. Регуляторы. Понятие о законах регулирования. Пропорциональные (П), интегральные (И), пропорционально-интегральные (ПИ), пропорционально-дифференциальные (ПД), пропорционально-интегродифференциальные (ПИД) регуляторы. Характеристики типовых законов регулирования.
Литература:[1, c. 103 – 131, 74 – 79], [5, c. 102 – 113]
6. Устойчивость систем автоматического регулирования (САР)
Понятие устойчивости. Устойчивость по Ляпунову. Алгебраический критерий устойчивости Рауса-Гурвица. Выбор параметров САР с помощью критериев устойчивости Рауса-Гурвица. Понятие о критическом (предельном) коэффициенте усиления. Частотные критерии устойчивости (Михайлова, Найквиста). Понятие о запасах устойчивости. Определение критического коэффициента усиления и запасов устойчивости по логарифмическим частотным характеристикам. Построение областей устойчивости.
Литература: [1, c. 179 – 214], [2, c. 101 – 120]
7. Качество процессов управления в автоматических системах
Понятие о качестве процессов управления в САР. Основные показатели качества. Оценка качества процессов управления по переходным функциям. Методы построения переходных функций по дифференциальным уравнениям и по вещественным частотным характеристикам (ВЧХ). Косвенные оценки показателей качества переходных процессов: по амплитудно-фазочастотной характеристике (АФЧХ), корневые методы, интегральные оценки. Диаграмма Вышнеградского. Точность САР в статике и режимах вынужденного движения.
Литература:[1, c. 93 – 149], [5, c. 61 – 113]
8. Коррекция динамических свойств и синтез систем управления
Понятие о демпфировании САР. Демпфирование подавлением высоких частот. Демпфирование введением положительного фазового сдвига. Демпфирование подавлением средних частот.
Общие методы повышения точности САР. Увеличение общего коэффициента усиления. Повышение порядка астатизма. Другие методы повышения точности.
Корректирующие звенья и способы их включения в систему. Последовательные и параллельные корректирующие устройства. Методы синтеза корректирующих устройств. Аналитическое определение передаточной функции корректирующего звена. Определение передаточной функции корректирующего звена с помощью ЛАЧХ. Построение желаемой ЛАЧХ.
Литература:[1, c. 150 – 194], [2, c. 101 – 123]
9. САУ с особыми свойствами
Определение нелинейных систем. Типы нелинейностей. Особенности нелинейных систем. Устойчивость нелинейных систем. Критерий устойчивости Попова.
Дискретные САУ. Понятие о дискретных системах. Классификация дискретных систем. Импульсные и цифровые системы. Устойчивость и качество линейных дискретных систем.
Классификация адаптивных САР. Методы построения беспоисковых систем и систем с поиском экстремума целевой функции. Общие сведения об оптимальном регулировании. Критерий оптимальности.
Литература:[1, c. 242 – 264, 289 – 290], [2, c. 194 – 336, 245 – 250]
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ЛАБОРАТОРНЫХ РАБОТ
1. Исследование синхронной передачи на сельсинах.
2. Исследование системы автоматического регулирования температуры
3. Экспериментальное определение динамических характеристик элементов системы регулирования.
4. Исследование астатической следящей системы автоматического регулирования измерительного устройства.
5. Исследование следящей системы автоматического регулирования с реостатной обратной связью.
6. Исследование дифференцирующих и интегрирующих динамических звеньев.
7. Определение статических характеристик реле.
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
1. Построение функциональных схем САУ.
2. Построение статических и астатических САР.
3. Составление дифференциальных уравнений динамических звеньев и систем.
4. Построение и преобразование структурных схем САУ, определение их передаточных функций.
5. Построение частотных характеристик динамических звеньев.
6. Определение устойчивости САУ.
7. Определение качественных показателей САР.
КУРСОВАЯ РАБОТА.
Цель курсовой работы – закрепить пройденный материал и проверить, насколько успешно студент-заочник ориентируется в литературе, рекомендуемой для изучения курса.
Содержание курсовой работы
В курсовой работе рассматривается силовая следящая САР угла поворота (см. рис. 2.17 электронного конспекта). Это может быть система на потенциометрах (рис. 2.18 электронного конспекта) или на сельсинах в трансформаторном режиме (рис. 2.23 и 2.24 электронного конспекта).
Курсовая работа включает следующие разделы.
Введение.
1. Описание проектируемой САР.
2. Составление математической модели исходной САР.
3. Оценка качества исходной САР.
4. Составление математической модели желаемой САР.
5. Коррекция исходной САР.
6. Оценка качества скорректированной САР.
Заключение.
В разделе «Введение» формулируются цели курсовой работы и решаемые задачи. Указывается дата выдачи задания и сроки выполнения.
В разделе 1 формулируется назначение системы, приводится ее схема (на сельсинах или на потенциометрах – на выбор) и описание работы.
В разделе 2 приводится структурная схема системы. Ее общий вид одинаков для всех вариантов:
Здесь W 1(p) – передаточная функция датчика рассогласования (моста на потенциометрах или пары сельсинов); W 2(p) – передаточная функция усилителя; W 3(p) – передаточная функция электродвигателя; W 4(p) – передаточная функция редуктора.
Вместо обозначений передаточных функций требуется подставить их выражения с числовыми значениями в соответствии с вариантом задания, например, вместо W 3(p) может быть записано 
и т. д.
После составления структурной схемы записываются передаточные функции для разомкнутого контура и замкнутой системы:
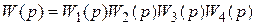– разомкнутый контур;
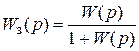– замкнутая система.
Например:
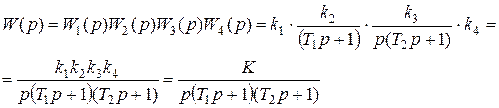
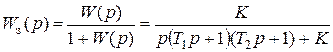и далее раскрыть скобки в знаменателе.
Здесь K – коэффициент передачи разомкнутого контура.
Естественно вместо всех k и T должны стоять числа в соответствии с заданием.
Для тех, кому лень читать конспект: p – это параметр дифференцирования, он остается в передаточных функциях в виде переменной.
Раздел 3 состоит из подразделов.
3.1. Оценка устойчивости исходной САР.
3.2. Частотные оценки качества.
3.3. Оценка качества по переходному процессу.
3.4. Выводы.
В подразделе 3.1 выполняется оценка устойчивости исходной САР по критерию Гурвица (см. электронный конспект). Требуется получить ответы на вопросы, устойчива ли система и чему равен критический коэффициент передачи (при котором система находится на границе устойчивости).
Если исходная система неустойчива, требуется уменьшить коэффициент передачи K до величины, обеспечивающей устойчивую работу с заданным перерегулированием. Для этого нужно построить модель системы в программе VisSim и подобрать нужный коэффициент передачи усилителя, ориентируясь на вид переходного процесса в окне Plot.
В подразделе 3.2 требуется построение следующих частотных характеристик: диаграмма Боде (то есть ЛАЧХ и ЛФЧХ разомкнутого контура), АЧХ замкнутой системы. Если исходная система была неустойчивой, то все в этом и следующем подразделе выполняется для системы с уменьшенным коэффициентом передачи (см. предыдущий абзац)!!!
ЛАЧХ и ЛФЧХ можно построить в программе VisSim, для чего нужно выделить разомкнутый контур и выбрать в меню Analyze – Frequency Response (предварительно нужно задать диапазон частот в меню Analyze – Frequency Range). Слева показана ЛАЧХ, справа ЛФЧХ (фазовый сдвиг в градусах, можно изменить на радианы в меню Analyze –Preferences):
По полученным графикам можно определить запасы устойчивости по критерию Найквиста (см. рис. 4.12 электронного конспекта).
Асимптотическая ЛАЧХ все равно должна быть построена вручную, так как потребуется для коррекции САР.
Указания по построению аппроксимирующих ЛАЧХ
График строится в координатной системе, в которой по оси абсцисс откладывается частота в логарифмическом масштабе, по вертикальной – усиление в дБ. Так как логарифм нуля равен минус бесконечности, за условное начало координат принимается w = 1 с–1. Через равные интервалы частота увеличивается в 10 раз. Эти интервалы называются декадами (границы декад вправо от начала координат 1, 10, 100, 1000 и т. д.). Аппроксимирующая ЛАЧХ имеет вид ломаной, участки которой имеют наклоны, кратные величине 20 дБ/дек, что соответствует изменению усиления на 20 дБ на протяжении 1 декады. То есть участки ЛАЧХ параллельны соответствующим линиям на рисунке:
Для построения графика делают следующее:
а) Определяются значения сопрягающих частот wсопр.i, в которых ЛАЧХ имеет изломы. По оси абсцисс в логарифмическом масштабе откладываются значения сопрягающих частот полученных по выражению
wсопр.i =1/Тi
где Тi – постоянная времени динамического звена.
б) Построить низкочастотную прямую ЛАЧХ для значений w < wсопр.min с наклоном – 20m дБ/дек, где m – число интегрирующих звеньев в главной цепи системы. Эта прямая при w = 1 должна иметь ординату, равную 20lgK, где К – коэффициент передачи разомкнутого контура.
в) Для каждой из сопрягающих частот wсопр.i изменить наклон ЛАЧХ по отношению к предшествующему участку, причем наклон характеристики зависит от вида звена для данной сопрягающей частоты. Для идеального дифференцирующего звена наклон изменяется на +20 дБ/дек; для апериодического и интегрирующего звеньев – на – 20 дБ/дек; для колебательного – на – 40 дБ/дек; для форсирующего – на +20 дБ/дек.
Пример.
Видно, что К = 10, в состав системы входит одно интегрирующее звено (m =1) и два апериодических с постоянными времени 0,25 с и 0,005 с.
Следовательно, на частоте w = 1 ордината ЛАЧХ 20lg K = 20lg10 = 20 дБ.
Сопрягающие частоты wсопр. i =1/ Тi равны 4 с–1 и 200 с–1 (расположены по возрастанию):
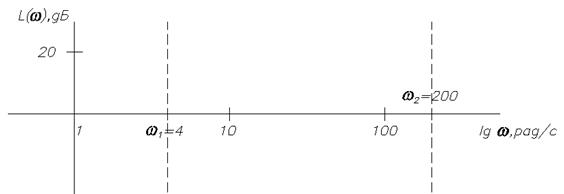
Низкочастотная часть ЛАЧХ (от –∞ до 4 с–1) имеет наклон –20m = –20дБ/дек, то есть на протяжении одной декады уровень уменьшается на 20 дБ.
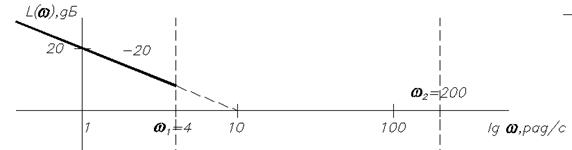
От 4 с–1 до 200 с–1 наклон определяется звеном, из которого получена частота 4 с–1, то есть апериодическим. Оно приводит к изменению наклона на –20 дБ/дек, то есть наклон равен –40 дБ/дек.
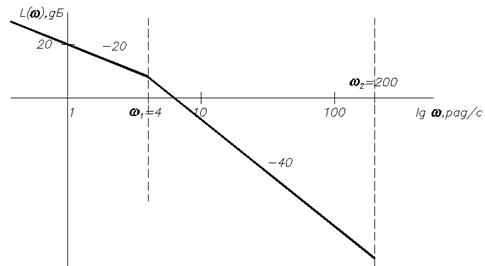
Аналогично рассуждая получаем наклон на участке от 200 с–1 до ∞ равным минус 60 дб/дек.
График имеет вид
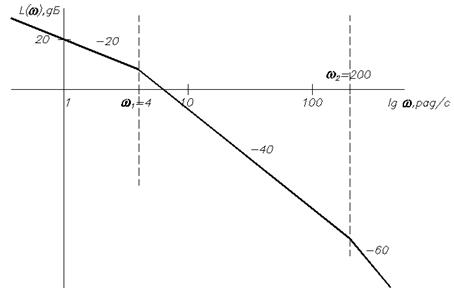
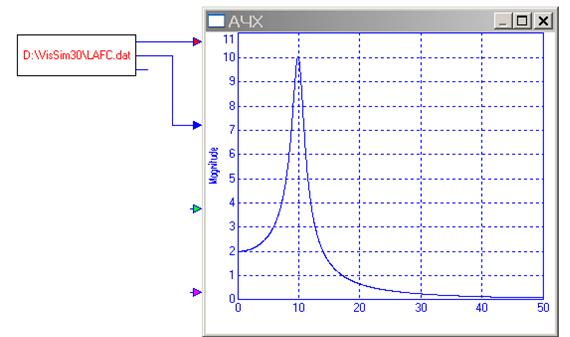
В программе VisSim получить АЧХ можно так же как ЛАЧХ, только при этом выделить всю систему. В полученном графике нужно убрать логарифмический масштаб (птички в полях LogX, LogY, DecibelY в свойствах графика):
По полученному графику оценивают показатель колебательности и время переходного процесса (см. электронный конспект, частотные критерии качества).
По полученному показателю колебательности нужно оценить перерегулирование в системе с помощью диаграммы:
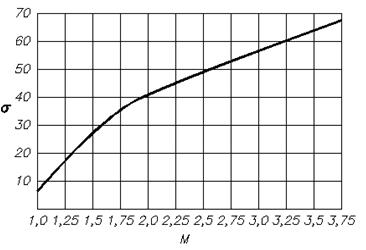
ВНИМАНИЕ! Описанным выше способом правильный график АЧХ не получится, так как частоты пересчитываются из логарифмического в обычный масштаб неверно! Поэтому полученное время переходного процесса будет некорректным, но показатель колебательности будет получен правильно.
Для любителей все делать правильно. Для корректного построения характеристик можно экспортировать ЛАЧХ в dat-файл, а затем воспроизвести график из файла. Для этого в свойствах осциллографа Plot Properties необходимо нажать кнопку Save Data to File. Сохраним значения ЛАЧХ в файле LAFC.dat и откроем его в Microsoft Word. Как видно, файл содержит два столбца цифр, разделенных двойной запятой.
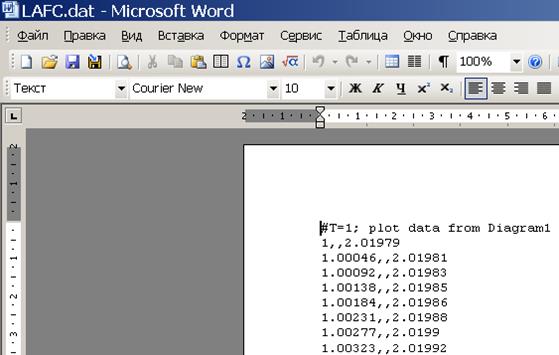
Рис. 55
В левом столбце записаны значения частоты, в правом – ординаты графиков, причем для ЛАЧХ масштаб нормальный, несмотря на то, что экспортируемый график имел логарифмический масштаб. Для импорта данных обратно в VisSim следует разделитель в виде двойной запятой заменить средствами Microsoft Word на пробел и сохранить файл.
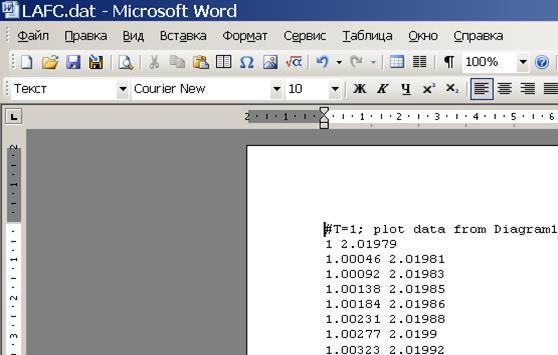
Рис. 56
Теперь в VisSim можно строить АЧХ и ФЧХ. Для этого поместим на поле программы осциллограф (Plot) и блок import (меню Blocks – Signal Producer – import). Соединим два верхних вывода блока с осциллографом и в настройках блока нажав кнопку Select File... выберем нужный dat-файл.
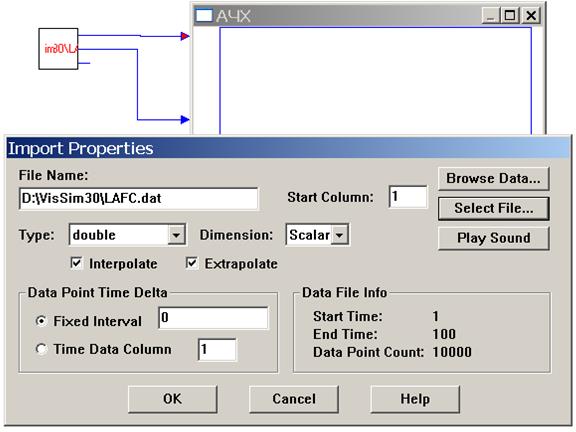
Рис. 57
В блоке import появится имя и путь к файлу. В меню Simulate – Simulation properties зададим время симуляции 0…100, которое в данном случае будет являться значениями частоты. В свойствах осциллографа на вкладке Options установим отметку в поле XY Plot, на вкладке Axis нужные пределы. Запустим симуляцию и получаем график.
В подразделе 3.3 требуется построить переходный процесс с использованием математических пакетов (например MathCAD или MATLAB) по формуле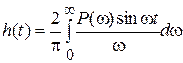 
или моделированием в VisSim (так проще):
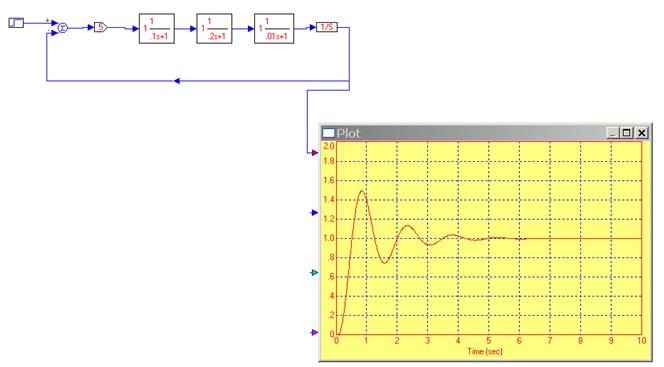
По переходному процессу определяются показатели качества в соответствии с электронным конспектом (рис. 4.29 электронного конспекта).
В подразделе 3.4 делаются выводы о соответствии показателей качества исходной системы требованиям задания на проектирование и о необходимости коррекции.
В разделе 4 выполняется построение желаемой ЛАЧХ и запись по ней желаемой передаточной функции.
Построение желаемой ЛАЧХ выполняют по участкам.
Низкочастотный участок строится по заданным требованиям точности. Для этого рассчитывают координаты рабочей точки A р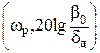 
. Рабочая частота – это максимальная частота входного синусоидального сигнала, при котором динамическая ошибка системы dд ещё не должна быть больше заданной. При проектировании следящей системы угла поворота с астатизмом первого порядка:
где Wmax – максимальная частота вращения вала; emax – его максимальное угловое ускорение.
Амплитуда входного сигнала определяется по формуле:
рад.
Низкочастотный участок проводят через рабочую точку (или на 3 дБ выше, чтобы учесть погрешность аппроксимации ЛАЧХ ломаной). Для системы с астатизмом 1-го порядка НЧ участок имеет вид прямой со спадом –20 дБ/дек:
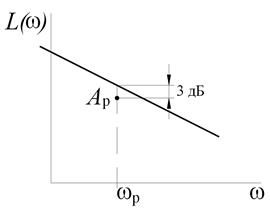
Среднечастотный участок строится по заданным показателям быстродействия и запасов устойчивости. Например, если задано время регулирования t р и перерегулирование s, частоту среза найдем, исходя из заданного времени переходного процесса tp:
,
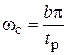где b – коэффициент, находимый из номограммы Солодовникова по допустимому перерегулированию s. Номограмма Солодовникова показана ниже:
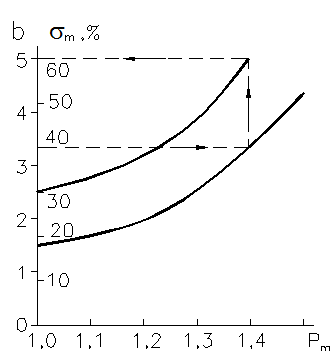
Номограмма Солодовникова и пример определения по ней коэффициента b при σ = 40%; (Рm – значение максимума ВЧХ)
Частоты начала и конца среднечастотного участка ЖЛАЧХ определим по уравнениям (DF – необходимый запас по фазе):
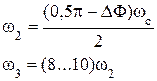
Среднечастотный участок проводится через частоту среза под наклоном –20 дБ/дек (рис. 5.7).
Рис. 5.7. Среднечастотная часть желаемой ЛАЧХ
НЧ и СЧ участки соединяются участком под наклоном –40 дБ/дек (если при этом рабочая точка оказывается выше графика, выбирается больший наклон).
Высокочастотный участок определяет интенсивность подавления помех и проводится параллельно высокочастотному участку исходной ЛАЧХ (т. е. –60 или –80 дБ/дек в зависимости от вида исходной ЛАЧХ).
В итоге желаемая ЛАЧХ для системы с астатизмом 1-го порядка имеет вид:
По желаемой ЛАЧХ можно записать передаточную функцию желаемой системы:
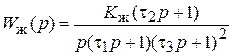, где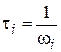 
.
Для проверки можно создать модель желаемой системы в программе VisSim и построить переходный процесс. Если он неудовлетворительный, то нужно уменьшать τ3 (то есть увеличивать ω3) до получения удовлетворительного переходного процесса.
В разделе 5 производится выбор корректирующих звеньев.
Ниже показан пример коррекции для системы с усилителем, имеющим передаточную функцию вида 
.
Для выбора способа коррекции системы изобразим ЛАЧХ исходной системы и ЖЛАЧХ в одних координатах:
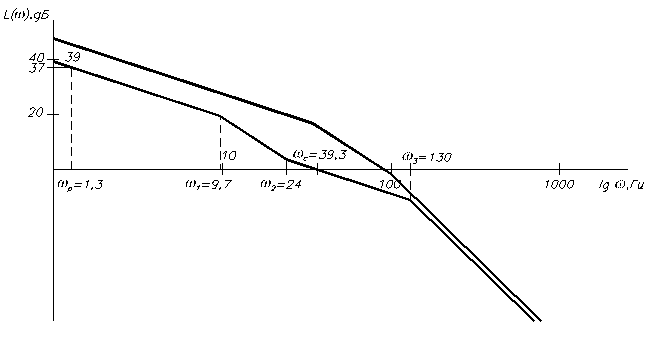
Опустим ЛАЧХ исходной системы вниз до совпадения низкочастотных участков. Это будет означать снижение коэффициента передачи системы до значения 89,1:
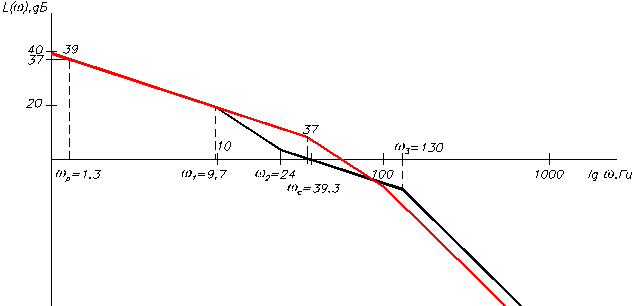
Для простоты реализации коррекции системы выбираем следующие корректирующие звенья:
Двигатель с передаточной функцией 
охватываем местной обратной связью таким образом, чтобы в результате получилось звено с передаточной функцией 
, т.е. постоянная времени двигателя увеличилась. Это необходимо для того, чтобы перегиб с –20 на –40 дБ/дек происходил на частоте w = 9,7 Гц, а не на частоте w = 37 Гц.
Обозначим через Z(p) передаточную функцию ОС. Тогда:
Приравняем W3(p) к требуемой функции W3’(p) и выразим из этого уравнения Z(p):
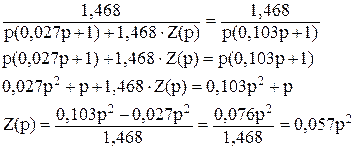
Таким образом, мы нашли передаточную функцию звена обратной связи. Для реализации этого звена необходимо учесть, что мы охватываем обратной связью двигатель, у которого выходной величиной является угол поворота вала, а входной – электрическое напряжение. Поэтому на выходной вал необходимо установить тахогенератор постоянного тока. Напряжение на его обмотках будет пропорционально угловой скорости, т.е. его передаточная функция Wос1 = kтг∙р. Выберем тахогенератор с крутизной характеристики kтг = 0,1 B∙c/рад. Последовательно тахогенератору необходимо включить еще одно дифференцирующее звено на операционном усилителе, на вход которого включен конденсатор. Это будет соответствовать звену с передаточной функцией Wос2 = k∙p. Найдем параметр k этого звена.
Передаточная функция всей ОС – 0,057p2, тахогенератора – 0,1p. Поэтому Т = 0,057/0,1=0,57 с. Схема дифференцирующей цепи показана ниже:
Инвертор на втором операционном усилителе предназначен для инвертирования выходного сигнала после первого ОУ, который тоже является инвертирующим.
Полагая R = 10 кОм, получим С = 57 мФ.
Функциональная схема двигателя, охваченного местной ОС:
После выполнения этой операции график ЛАЧХ изменится следующим образом:
Второе корректирующее звено включим в местную ОС с тиристорным усилителем для уменьшения его постоянной времени с 0,01 до 0,0077. Это приведёт к тому, что перегиб с –40 до –60 дБ/дек будет на частоте w2=130 Гц, а не на частоте 100 Гц.
В качестве звена применим пропорциональное звено с неизвестным пока коэффициентом усиления kос.
Для его расчета запишем передаточную функцию звена, охваченного ОС:
Таким образом, новое значение параметра Т будет равно 0,01/(1+200kос). Приравняв его к требуемому 0,0077, найдем kос:
Новый коэффициент усилителя с ОС будет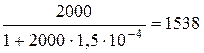 
Новая передаточная функция 
.
График ЛАЧХ теперь выглядит следующим образом:
Остальную коррекцию выполним с помощью последовательных корректирующих звеньев.
С учетом произведенной коррекции в пунктах разомкнутая система будет иметь следующую передаточную функцию:
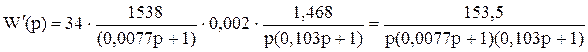
Передаточную функцию желаемой ЛАЧХ разомкнутой системы мы нашли выше:
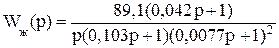
Обозначим через Z(p) передаточную функцию последовательного корректирующего устройства.
Так как W¢(p) *Z(p) = Wж(p), то
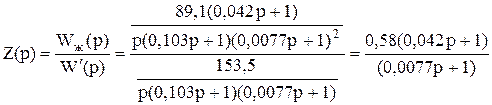
Такое корректирующее звено можно реализовать с помощью типовой RC-цепи.
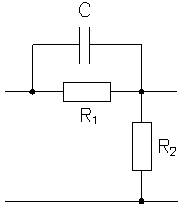
Передаточная функция такого звена 
T1 = 0,042
T2 = 0,0077
Найдем параметры цепи, полагая R1 = 1 кОм:
T1 = R1C C = T1/R1 = 0,042/1000 = 42 мФ
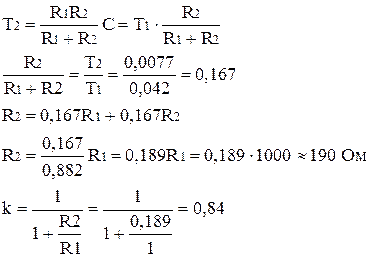
Структурная схема скорректированной САР выглядит следующим образом:
Передаточная функция разомкнутой системы определена выше:
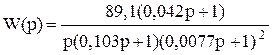
Для замкнутой системы передаточная функция:
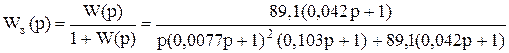
В заключении перечисляются выполненные работы и делается вывод об успешной коррекции САР.
Литература
1. Солодовников В.В., Плотников В.Н., Яковлев А.В. Основы теории и элементы систем автоматического регулирования. – М.: Машиностроение, 1985.
2. Теория автоматического управления/Под ред. Воронова А.А. – М.: Высшая школа, ч. 1, 2. – 1986.
3. Ильин В.В. Телеуправление и телеизмерение: Уч. пособие для вузов. – М.: Энергоиздат, 1982. – 560 с.
4. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – М.: Наука, 1975. – 768 с.
5. Топчеев Ю.И. Атлас для проектирования систем автоматического регулирования: Учеб. пособие для втузов. – М.:Машиностроение, 1978.
6. Минченя В.Т., Савченко А.Л. Основы автоматики. Лабораторный практикум. Ч.1. – Минск, 2002.
7. Теория автоматического управления. Учебник/Под ред. А.В.Нетушила. – М.: Высшая школа, 1983. – 432 с.
