Лекция №6. Центр параллельных сил. Центр тяжести. Определение координат центра тяжести.
Центр параллельных сил.
Рассмотрим две параллельные силы 
и 
, приложенные к телу в точках 
и 
. Очевидно, что эти силы имеют равнодействующую, линия действия которой параллельна слагаемым силам, и проходит через точку 
, положение которой определяется по формуле:
. (6.1)
Если рассматриваемые силы 
и повернуть в одну и ту же сторону на один и тот же угол, то образуются две новые силы 
и 
, имеющие те же модули. Следовательно, равенство (6.1) сохранится, и линия действия равнодействующей 
также пройдет через точку . Такая точка называется центром параллельных сил и .
Если рассматривать систему 
сил, то получим аналогичную ситуацию.
Точка , через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах этих сил около точек приложения в одну и ту же сторону на один и тот же угол, называется центром параллельных сил.
Найдем координаты центра параллельных сил. Положение точки по отношению к телу является неизменным, и от выбора системы координат зависеть не будет. Возьмем произвольные координатные оси 
и обозначим в этих осях точки: 
и приложим к ним силы 
.
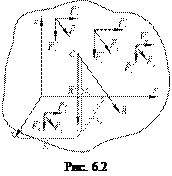Пусть равнодействующая 
этих сил проходит через точку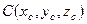 
. Повернем эти силы около точек приложения так, чтобы они стали параллельны оси 
, и применим к повернутым силам 
теорему Вариньона. Т.к. является равнодействующей для этих сил, то, беря моменты относительно оси 
, найдем, что
. (6.2)
Но из чертежа видно, что 
, аналогично, 
, 
, …, 
. Подставляя эти величины в равенство (6.2), получим
.
Отсюда 
.
Для координаты 
аналогичную формулу найдем, беря моменты относительно оси 
. Чтобы определить 
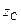, повернем опять все силы, сделав их параллельными оси , и применим к этим силам теорему Вариньона, беря моменты относительно оси :
,
откуда определим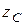 
.
Таким образом, координаты центра параллельных сил определяются по формулам:
, (6.3)
где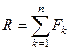 
.
Силовое поле. Центр тяжести.
Область, в каждой точке которой на материальное тело действует сила, называется силовым полем.
На каждую точку тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила, которую называют силой тяжести.
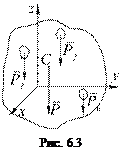Поле тяжести, в котором силы тяжести, действующие на частицы тела, можно считать параллельными и сохраняющими для каждой частицы постоянное значение при любых поворотах тела, называют однородным полем тяжести.
Равнодействующую сил тяжести 
, действующих на частицы данного тела, обозначим 
. При любом повороте тела силы остаются приложенными в одних и тех же точках тела и параллельными друг другу.
Следовательно, равнодействующая 
при любых поворотах тела будет проходить через одну и ту же неизменно связанную с телом точку , являющуюся центром параллельных сил тяжести . Эта точка и называется центром тяжести.
Центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве.
Координаты центра тяжести, как центра параллельных сил, находятся по формулам:
, (6.4)
- координаты точек приложения сил тяжести 
, действующих на частицы тела.
