Жұмысты орындау реті. 1) ЛАБ3 бағдарламасын іске қосып, сынақ кітапшаңыздың нөмірі бойынша тіркеліңіз.

1) ЛАБ3 бағдарламасын іске қосып, сынақ кітапшаңыздың нөмірі бойынша тіркеліңіз.

2) Зерттелетін QA және Y кездейсоқ шамаларын таідап алыңыз.

3) Екі кездейсоқ шамалардың (12-18 значений) көрсеткіштерін тіркеңіз.

4) Қолмен немесе MsExcel не Mathcad жүйелерін пайдаланып қажетті барлық есептеулерді орындаңыз.

5) Осыған ұқсама көрсеткіштерді QB және Y кездейсоқ шамалар үшін алыңыз.

6) Қолмен немесе MsExcel не Mathcad жүйелерін пайдаланып қажетті барлық есептеулерді орындаңыз.

7) Оқытушы ұсынған жұмысты орындау бақылау мысалды қолданыңыз.

Әдебиет:

негізгі:

1. Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с.

2. Инков А.М. Моделирование и идентификация объектов управления. Методические указания к выполнению лабораторных работ для студентов спец. 050702. Шымкент, ЮКГУ, 2010 г., -78 с.

қосымша:

3. Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с.

4. Построение математических моделей химико-технологических процессов. Под ред. Дудникова Е.Г. - Л.: Химия, 1970. –312 с.

5. Райбман Н.С., Чадеев В.М. Построение моделей производства. - М.: Энергия, 1975.

Бақылау (сұрақтар, тесттер, тапсырмалар және т.б.)

1) Кездейсоқ шама дегеніміз не?

2) Кездейсоқ шамалардың түрлері?

3) Генеральды жиынтық (совокупность) дегеніміз не?

4) Кездейсоқ таңдама (выборка) дегеніміз не?

5) Қандай таңдама репрезентативтік деп аталады?

6) Кездейсоқ шаманың таралу заңы, таралу функциясы және таралу тығыздығы деп нені атаймыз?

7) Математикалық күтім дегеніміз не және ол нені сипаттайды?

8) Дисперсия дегеніміз не және ол нені сипаттайды?

9) Орташа квадратты ауытқу (стандарт) дегеніміз не және ол нені сипаттайды?

10) Корреляцияның коэффициенті дегеніміз не және ол нені сипаттайды?

11) Кездейсоқ шаманың қандай бағасы бақуатты (состоятельная), жылжымаған болып табылады?

12) Сенімді ықтималдық, маңыздылық деңгейі дегеніміз не?

13) Еркіндік дәрежесі дегеніміз не және ол қалай анықталады?

14) Сенімді аралық, сенімді шекаралар дегеніміз не?

15) Математикалық күтім үшін сенімді аралық қалай анықталады?

16) Дисперсия үшін сенімді аралық қалай анықталады?

17) Статистикалық гипотеза дегеніміз не?

18) Математикалық күтімнің С санына тең болуы жөніндегі гипотеза.

19) Екі кездейсоқ шамалардың математикалық күтімдерінің бір біріне тең болуы жөніндегі гипотеза.

20) Екі кездейсоқ шамалардың дисперсияларының бір біріне тең болуы жөніндегі гипотеза.

21) Екі кездейсоқ шамалар арасында корреляцияның жок болуы жөніндегі гипотеза.

 

Тақырыб 4: Регрессиялық модельдің параметрлерін анықтау. Белсенді эксперименттің деректері бойынша басқару объектінің статикалық модельдерін құру (экспериментті жоспарлау әдістері)

 

Мақсаты: Жұмыстың мақсаты эксперименттерді жоспарлауды пайдаланып, белсенді эксперимент әдістері арқылы регрессиялық модельдің параметрлерін анықтау болып табылады. Студент «Регрессиялық модельдің параметрлерін анықтау. Белсенді эксперименттің деректері бойынша басқару объектінің статикасының модельдерін құру (экспериментті жоспарлау әдістері)» тақырыбын оқу барысында алған білімдерін пайдалана білуі керек.

 

Оқыту мақсаты:

Студент білуге тиіс:

§ белсенді эксперимент әдістерін;

§ регрессиялық модельді;

§ экспериментті жоспарлау әдістерін.

Студент істей алуға тиіс:

§ экспериментті жоспарлауды жүргізу;

§ регрессиялық модельдің параметрлерін анықтау;

§ басқару объектінің статикасының модельдерін құру.

 

Тақырыптың негізгі сұрақтары:

Базалық

§ критикалық мәндер;

§ Кохрен критерийі;

§ Фишер критерийі.

Негізгі

§ жоспарлау матрицасы;

§ адекваттылық дисперсиясы.

Теориялық негіздері

Жоспарлау матрицасындағы әр тәжірибе m рет қайталанылатын жоспарланған экспериментті дисперсиялық және регрессиялық талдау сұлбасының жалпы түрі келесі:

Сызықты жоспар 2^К

Эксперименттің жоспары 4.1 кестеде келтірілген.

Кесте. 4.1

Тәжірибе №	x0	x1	x2	...	xk	Y		σY2
	+1	+1	-1	.	+1	y11,y12,...,y1m	y1	σ12
	+1	-1	-1	.	+1	y21,y22,...,y2m	y2	σ22
	+1	+1	+1	.	+1	y31,y32,...,y3m	y3	σ32
.	.	.	.	.		.	.
.	.	.	.	.		.	.
.	.	.	.	.		.	.
N	+1	-1	+1	.	-1	yN1,yN2,...,yNm	y4	σN2

1) Қажетті эксперименттер жүргізіледі.

2) Кохрен критериі бойынша таңдама дисперсиялардың біртектілігі тексеріледі. Ол үшін максималды дисперсияның барлық дисперсиялардың қосындысына қатынас құрастырылады:

 

Пайда болған қатынасты кестелік мәнбен салыстырады: Gкр=G(α, f₁, f₂), бұл жерде: α=0.05, f₁ = m - 1, f₂ = N. Егер G<G_kp болса, онда дисперсиялар біртекті.

Онда ұдайы өңдірілудің (воспроизводимость) дисперсиясы ретінде еркіндік дәрежелер саны f_вос = N(m-1) болатын орташа дисперсиясын алуға болады:

 

(4.3)

 

3) Регрессия теңдеуінің коэффициенттері келесі формула бойынша анықталады:

 

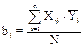
(4.4)

 

 

4) Коэффициенттердің дисперсиясы келесідей анықталады:

σ_Bj² = σ_ВОС²/(N·m) (4.5)

5) Коэффициенттердің мағыналығы Стьюдент критериі бойынша тексеріледі. Регрессия теңдеуінің барлық коэффициенттері үшін t-қатынасы құрастырылады:

t_j = |b_j|/σ_Bj (4.6),

оны мағыналық деңгейі σ =0.05 және еркіндік дәрежелер саны f=N(m-1) үшін кестелік tkp=t(α, f) мен салыстырады. Егер t_j < tkp болса, онда сәйкесінші b_j коэффициенті мағынасыз ретінде регрессия теңдеуінен алып тасталады.

6) Регрессия теңдеуінің экспериментке адекватты болуы Фишер критериі бойынша тексеріледі. Дисперсияны тексеру үшін дисперсиялық қатынас құрастырылады:

F = σ_АД²/σ_ВОС²,

бұл жерде: σ_АД² – адекваттылық дисперсиясы, ол келесі формула бойынша анықталады:

 

(4.7)

 

 

l - Регрессия теңдеуінің мағыналы коэффициенттерінің саны.

Егер пайда болған дисперсиялық қатынас кестелік Fkp=F(α, f_ад, f_вос) (α =0.05, f_ад=N - l, f_вос=N(m-1)) аз болса, онда теңдеу экспериментке адекватты, керісінше жағдайда экспериментті адекватты сипаттау үшін аппроксимациялаушы полиномның ретін жоғарылату керек.

2 ретті ортогональды жоспар

Кесте. 4.2.

Тәжірибе №	x0	x1	x2	.	xk	x1'	x2'	.	xk'	Y		σY2
	+1	+1	-1	.	+1	x11'	x21'	.	xk1'	y11,y12,..,y1m	y1	σ12
	+1	-1	-1	.	+1	x12'	x22'	.	xk2'	y21,y22,..,y2m	y2	σ22
	+1	+1	+1	.	+1	x13'	x23'	.	xk3'	y31,y32,,y3m	y3	σ32
.	.	.	.	.		.	.	.	.	.	.	-
.	.	.	.	.		.	.	.	.	.	.	-
.	.	.	.	.		.	.	.	.	.	.	-
N	+1	-1	+1	.	-1	x1N'	x2N'	.	xkN'	yN1,yN2,,yNm	yN	σN2
N+1	+a			.		.	.	.	.	.	.	-
N+2	-a			.		.	.	.	.	.	.	-
N+3		+a		.		.	.	.	.	.	.	-
N+4		-a		.		.	.	.	.	.	.	-
N+5			+a	.		.	.	.	.	.	.	-
N+6			-a	.		.	.	.	.	.	.	-
.	.	.	.	.	.	.	.	.	.	.	.	-
.					+a	.	.	.	.	.	.	-
N+2·k					-a	.	.	.	.	.	.	-
N+2·k+1						x1n'	x2n'	.	x3n'	yn1,yn2,,ynm	yn	σn2

 

Тәжірибе саны 2^k + 2·k + 1 ретінде анықталады.

Жоспардың негізін сызықтық 2^k (жолдары 1 ден N дейін) жоспары құрайды. Сонымен қатар, тәжірибелер жұлдыздық нүктелер мен (жолдар N+1 ден N+2·k дейін) жоспардың орталығында (N+2·k+1 жолы) жүргізіледі.

X_j' бағандары келесі формула бойынша анықталады:

 

(4.8)

 

1) Өлшенетін шаманың орташа мәні мен дисперсиясы (4.1), (4.2) формулалары бойынша анқталады.

2) Кохрен критериі бойынша таңдамалы дисперсиялардың біртектілігі тексеріледі. Ұдайы өңдірілу дисперсиясы (4.3) бойынша есептеледі.

3) Регрессия теңдеуінің коэффициенттері келесі формула бойынша анықталады:

 

(4.9)

 

4) Коэффициенттердің дисперсиясы келесідей анықталады:

 

 

(4.10)

 

 

5) Коэффициенттерді мағыналыққа тексеру әдістемесі жоғарыда көрсетілген (4.6 формуласын көр).

6) Регрессия теңдеуінің экспериментке адекватты болуын тексеру жоғарыда көрсетілген (4.7 формуласын көр).

 

Білім берудің және оқытудың әдістері: Бақылау сұрақтар мен жүргізілген жұмыс туралы әзірленген есеп бойынша ауызша сұрау.Жұмысты өзіндік орындау