Основным параметром, характеризующим однофазный трансформатор, является коэффициент трансформации
n = U1н / U2н = w1 / w2.
При работе однофазного трансформатора под нагрузкой в номинальном режиме из сети потребляется полная мощность
Sн = U1н + I1н = U2н + I2н.
Коэффициент полезного действия трансформатора определяется отношением активной мощности, отдаваемой в нагрузку, Р2 к активной мощности, потребляемой трансформатором из сети, Р1:
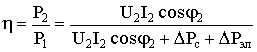 ,
,
где: ∆Рст – потери в магнитопроводе (постоянные);
∆Рэл – потери в обмотках, зависящие от тока нагрузки.
Величина ∆Рст определяется по данным режима (опыта) холостого хода трансформатора. Трансформатор в режиме холостого хода потребляет из сети, главным образом, реактивную мощность на создание магнитного потока в магнитопроводе. Активная мощность Р0 относительно невелика и обусловлена потерями от вихревых токов и на гистерезис в стали магнитопровода
∆Рст = Р0 = U1н I0 cos φ10.
Величина ∆Рэл определяется в опыте короткого замыкания. В этом опыте вторичная обмотка замыкается накоротко, на первичную обмотку подается пониженное напряжение U1к такой величины, чтобы токи в обмотках трансформатора были равны номинальным I1н и I2н. В этом случае регистрируемая ваттметром активная мощность Рк равна (без учета потерь ∆Рст ≈ 0) электрическим потерям в обмотках ∆Рэл н, соответствующим номинальному режиму.
Рк = ∆Рэл н = U1н I1н cos φ1к.
В номинальном режиме КПД трансформатора определяется формулой
 .
.
Если нагрузка отличается от номинальной, мощность потерь в обмотках
∆Pэл = (I1 / I1н)2 Pк = β2 Pк,
при этом
 ,
,
где: β – коэффициент загрузки трансформатора.
По данным опытов холостого хода и короткого замыкания рассчитываются параметры схемы замещения трансформатора.
Сопротивления намагничивающей цепи:
Z0 = U1н / I0; R0 = P0 / I02; X0 = (Z02 - R02)1/2.
Сопротивления короткого замыкания:
Zк = U1к / I1н; Rк = Pк / I1н2; Xк = (Zк2 - Rк2)1/2.
Сопротивления первичной обмотки:
R1 = R'2 = Rк / 2; X1 = X'2 = Xк / 2.
Работа трансформатора под нагрузкой определяется его внешней характеристикой
U2 = F(I2) или U2 = F(β).
Из уравнения электрического состояния для вторичной обмотки трансформатора
É2 = Ú2 + Í2 Z2
запишем уравнение для внешней характеристики трансформатора
Ú2 = É2 - Í2 Z2 = Ú2н - Í2 Z2,
где: É2 = Ú2н.
Напряжение на зажимах вторичной обмотки трансформатора определяем по формуле
U2 = (100 - ∆U2%) U2н / 100.
Относительное изменение напряжения во вторичной обмотке ∆U2 определяется соотношением
∆U2 = β (Uа cos φ2 + Uр sin φ2),
где: Uа = (Pк / Sн) 100% – активная составляющая напряжения короткого замыкания;
Uр = (Uк2 - Ua2)1/2 – реактивная составляющая напряжения короткого замыкания.
При активно-индуктивной нагрузке трансформатора Zн и известном cosφн для вторичной цепи трансформатора можно записать уравнение по второму закону Кирхгофа
É2 = Í2 Z2 + Í2 Z2н.
Ток во вторичной обмотке трансформатора I2 = I2н и может быть рассчитан по формуле
 .
.
Трехфазным трансформаторы характеризуются фазный nф и линейный nл коэффициенты трансформации:
nф = U1ф / U2ф = w1 / w2; nл = U1л / U2л.
Соотношение между линейным и фазным коэффициентами трансформации зависит от схем соединения обмоток трансформатора. При схемах соединения «звезда-звезда» (Y = Y) или «треугольник-треугольник» (Δ = Δ) линейные и фазные коэффициенты одинаковы (Кл = Кф). При схеме соединения  . При схеме соединения
. При схеме соединения  .
.
Полная мощность трехфазного трансформатора определяется соотношением
 .
.
Коэффициент полезного действия рассчитывается также как для однофазного трансформатора
Построение внешней характеристики U2 = F(I2) и рабочей характеристики η2 = f(I2) производится по вышеприведенным соотношениям при изменении тока нагрузки Iн = I2 от I2 = 0 (режим холостого хода) до I2 = 1,2 I2н или при изменении коэффициента нагрузки β от β = 0 до β = 1,25 βн.




