Основные понятия комбинаторики
В разделе математики, который называется комбинаторикой, решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств
Например,возьмём 10 различных цифр 0,1,2,3,…….9 и составим из них комбинации различных чисел: 345, 23, 32, 5036, 1248
Назовите комбинации, которые отличаются
--порядком
--числом цифр
--входящими в них цифрами
Таким образом, полученные комбинации удовлетворяют различным условиям. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания. Рассмотрим их отдельно. Предварительно познакомимся с понятием факториала.
Понятие факториала
Определение. Произведение всех натуральных чисел от 1 до п
включительно называют n- Факториалом и пишут
n! = 1 • 2 • 3 • 4 •... • (n -1) • n
Считают,что 1!=1; 0!=1
ПРИМЕРЫ:
Вычислить:
3! = 1* 2*3=6
8!= 5!*6*7*8 =6!*7*8
7!- 5! = 5!*6*7 – 5! = 5! (6*7-1)= 1*2*3*4*5*(41)=120*41=4920
 = (5!*6*7 + 5!) / 5!*6 = 5! (6*7+1) / 5!*6 =43/6
= (5!*6*7 + 5!) / 5!*6 = 5! (6*7+1) / 5!*6 =43/6
Вычилить:
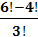 ,
,  ,
, 

Перестановки
Пример: Пусть даны три буквы А, В, С.
Составим всевозможные комбинации из этих букв.(например АВС)
Определение Комбинации из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.
Перестановки обозначаются символом Рn, где n - число элементов, входящих в каждую перестановку
Число перестановок можно вычислить по формуле
Рn = n!
Пример: Сколько различных пятизначных чисел можно составить из цифр 1,2,3,4,5 при условии, что ни одна цифра в числе не повторяется?
Размещения
Пример: Пусть имеются четыре буквы A, B, C, D.
Составить комбинации только из двух букв .( например АВ, ВА )
Определение Комбинации из m элементов по n элементов, которые отличаются друг от друга или самими элементами, или порядком элементов, называются размещениями.
Размещения обозначаются символом  ,
,
где m - это число всех имеющихся элементов,
n - число элементов в каждой комбинации, (m≥n),
и вычисляются по формуле

Пример: Сколькодвузначных чисел можно составить из пяти цифр 1,2,3,4,5 при условии, что ни одна из них не повторяется.
Сочетания
Пример: Из четырех различных букв A, B, C, D
составить комбинации, которые отличающиеся друг от друга хотя бы одним элементом (например АВ,ВС)
Определение. Сочетаниями называют все комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом, ( n≤m).
Сочетания обозначаются символом  и вычисляются по формуле
и вычисляются по формуле

Пример: В ящике имеется 10 деталей. Сколькими способами можно выбрать две детали из этого ящика
Алгоритм решения задач по теме: «Комбинаторика»
1.Используют часть элементов?
/ \
Да Нет(все)- перестановки
I
2. Порядок элементов имеет значение?
/ \
Да- размещение Нет- сочетание
Примеры
1Сколькими способами из 7-ми человек можно выбрать комиссию, состоящую из 3 человек?
2.Сколько различных «слов» можно получить, переставляя буквы в слове СОЛНЦЕ?
3.Сколькими способами можно составить школьное расписание из шести предметов?
4.Сколькими способами можно выбрать четырёх участников из 15 членов сборной и расставить их для эстафеты 800+400+200+100 метров?
5.Сколько вариантов распределения трёх путевок в санаторий различного профиля можно составить для пяти претендентов?
6.Сколькими способами можно выбрать из 25 учащихся одного класса 5 человек для участия в интеллектуальном марафоне?
7.Сколькими способами могут быть выделены три призовых места среди 16 соревнующихся?
8.Сколькими способами можно заполнить билет «5 из 36»
9.Сколько можно составить сигналов из 6 флажков различного цвета, взятые по 2?
Многие комбинаторные задачи могут быть решены с помощью двух правил- правила умножения и правила сложения
Правило умножения: если из некоторого множества первый объект (элемент а) можно выбрать n способами, а второй объект (элемента b)- m способами, то оба объекта (a и b) в указанном порядке можно выбрать (n * m)
Правило сложения: если некоторый объект (элемент а) можно выбрать n способами, а второй объект (элемент b)- m способами, причем первые и вторые способы не пересекаются, то любой из объектов (a и b) можно выбрать (n+ m)
Примеры:
1. В вазе стоят 9 красных и 7 розовых гвоздик, Сколькими способами можно выбрать из нее:
а) 3 гвоздик,
б) 6 гвоздик одного;
г) 4 красных и 3 розовых гвоздик?
2. В ящике 15 деталей, среди которых 6 бракованных. Наудачу выбирается комплект из 5 деталей. Сколько всего комплектов, в каждом из которых 2 детали бракованные?
3. Группа туристов из 12 юношей и 7 девушек выбирают по жребию 5 человек для приготовления ужина. Сколько существует способов при которых в эту «пятерку» попадут:
| А) одни девушки В) 1 юноша и 4 девушки | Б) 3 юноши и 2 девушки Г) 5 юношей |
Основные понятия теории вероятностей
.
Теория вероятностей есть раздел математики, в котором изучаются случайные явления (события).
Фактор случайного события играет большую роль в науке, технике, жизни. Не является, например, строго определенным движение объекта в атмосфере. Так ветер, дождь, снег, другие факторы оказывают непредсказуемое воздействие на полет самолета, снаряда, ракеты.
| ^ |
Случайным является число пассажиров трамвая, спрос на тот или иной товар, количество слушателей концерта, номер выигравшего лотерейного билета, пол родившегося ребенка и т.д.
Для того, чтобы записывать и исследовать эти закономерности, введем некоторые основные понятия и определения.
1.2. Основные понятия и определения.
Основными понятиями в теории вероятностей являются понятия: событие и вероятность события.
Определение 1. Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием
Определение 2. Случайным событием будем считать событие, которое может либо произойти, либо не произойти в результате некоторого испытания
Определение 3. Если нас интересует какое-либо событие из всех возможных событий, то будем называть его искомым событием.
Определение 4. Все рассматриваемые события будем считать равновозможными. т.е. такими, которые имеют равные возможности произойти События принято обозначать заглавными буквами латинского алфавита А, В, С, D.
Определение 5. События называются несовместимыми, если ни какие два из них не могут произойти в данном опыте вместе.
В противном случае события называются совместимыми.
Определение 6. Событие называется достоверным, если оно обязательно происходит в данном испытании.
Достоверное событие обозначается буквой U.
Определение 7. Событие называется невозможным. если оно в данном опыте не может произойти.
Невозможное событие обозначается буквой V.
Определение 1. К Каждому случайному событию ставится в соответствие число 0≤ Р ≤1, которое называется вероятностью этого события.
Определение 2. Вероятность события А равна отношению числа исходов, благоприятствующих наступлению события А(m), к общему числу всех равновозможных исходов (n)
P(A) = m/n
Свойства:
1. Вероятность любого события есть неотрицательное число, не превосходящее единицы.
2. Вероятность достоверного события равна единице, т.к. n/n=1.
3. Вероятность невозможного события равна нулю, поскольку 0/n=0
Пример
1. Бросают игральную кость. Найти вероятность того, что:
А) выпадет чётное число очков
В) выпадет число очков кратное 3
Г) выпадет число очков кроме 5
2. Из букв А,С,Н,Н,А,А составляется слово, состоящее из букв. Какова вероятность того, что получится слово «АНАНАС»
3. В урне содержится 5 белых и 4 чёрных шара. Вынимается на удачу один шар. Найти вероятность того, что он белый
4. Дано шесть карточек с буквами Н,М,И,Я,Л,О Найти вероятность того, что:
А) получится слово ЛОМ
Б) получится слово МОЛНИЯ
5. В коробке 5 синих, 4 красных, и 3 зелёных карандаша. Наудачу вынимают 3 карандаша. Какова вероятность того, что:
А) все они одного цвета
В) все они разные
С) среди них 2 синих и 1 зелёный карандаш
6. Из 40 вопросов, входящих в экзаменационные билеты, студент знает 30. Найти вероятность того, что среди трёх наугад выбранных вопросов студент знает:
А) три вопроса
В) 2 вопроса
Г) 1 вопрос
В А Р И А Н Т №
1. Вероятность наступления некоторого события не может быть равна:
1.. 1/3 2. 1 3. 2 4. 0
2. Из слова «Абрикос»» выбирается наугад одна буква. Вероятность того, что она согласная буква равна……
1.. 2/7 2. 4/7 3. 3/7 4. 7/4
3. Невозможными являются следующие два события:
1. Появление двух очков при бросании трех игральных кубиков.
2. Появление не менее 3 и не более 18 очков при бросании трех игральных кубиков.
3. Появление 19 очков при бросании трех игральных кубиков.
4. Появление 12 очков при бросании трех игральных кубиков.
4. В урне находится 6 шаров (3 черных и 3 белых). Событие (А) заключается в том,что вынули белый шар.Событие (Б) – вынули черный шар. Опыт состоит в выборе только одного шара. Тогда для этих событий неверными будет утверждение:
1. А и Б равновероятны.
2. Вероятность события Б равна 1/2.
3. А и Б несовместны.
4. Событие А невозможно.
5. Игральный кубик бросают один раз. Тогда вероятность того, что на верхней грани выпадет число очков более трех, равна:
1. 0 2. 1/3 3. 1 4. 0,5
6. Число различных перестановок из букв слова «WORD» равно:
1. 20 2. 8 3. 12 4. 24
7.Количество перестановок из букв слова «вальс»,в которых буква «в» на первом месте, а буква
«с»-в конце слова, равно……
1. 24 2. 3 3. 6 4. 5






