Рассмотрим систему:
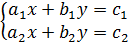
Графиком данной системы являются две прямые.
Выразим из уравнений y:
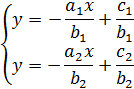
Система разрешима в целых числах тогда и только тогда, когда

5. Системы трёх уравнений с тремя неизвестными.
Рассмотрим систему:
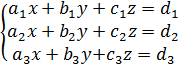
Графическим решением данной системы являются 3 плоскости.
Критерии:
1) Если все 3 плоскости параллельны, то решений нет.
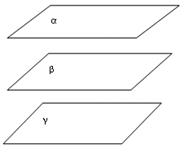
2) Если все 3 плоскости совпадают, то любая точка является решением
В данном случае для того, чтобы найти целочисленные решения системы достаточно решить одно уравнение системы.
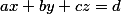
где  целые числа
целые числа
Общее решение у неизвестных может выглядеть так:

Подставим общее решение в уравнение
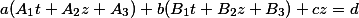
Сгруппируем по неизвестным, получим:
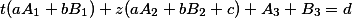
В правой части стоит постоянное число, обозначенное буквой d. Значит, от t оно не зависит, а значит
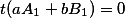
Логично предположить что и от z оно не зависит, а значит
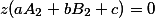
а вот от постоянных значений A3 и B3 оно зависит напрямую, то есть
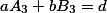
Получили три типовых классических диофантовых уравнений с двумя неизвестными, решение которых описано во втором пункте.
3) Если две плоскости пересекают третью, но не имеют общих точек, то решений нет.
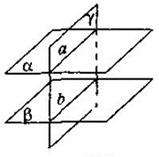
4) Если все плоскости пересекаются и проходят через одну прямую, то все точки прямой являются решением.
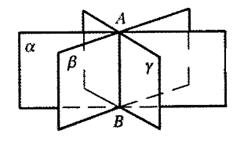
5) Если все плоскости пересекаются в одной точке, то решением является точка пересечения.
Заключение:
При рассмотрении вопроса разрешимости диофантовых уравнений можно воспользоваться тем, что любую систему таких уравнений можно преобразовать в одно диофантово уравнение в целых числах, разрешимое в том и только том случае, когда разрешима исходная система (при этом множество переменных и множество решений этого нового уравнения может оказаться совершенно другим).
Также, при рассмотрении вопроса разрешимости переменные часто разделяют на параметры (значения которых предполагаются фиксированными) и неизвестные. Таким образом, каждое диофантово уравнение определяет множество наборов параметров, при которых оно разрешимо относительно неизвестных, называемое диофантовым множеством. Рассматриваемое диофантово уравнение называется диофантовым представлением этого множества. Важный результат, состоит в том, что каждое перечислимое множество имеет диофантово представление.
Список литературы:
1) Гельфонд А.О. «Решение уравнений в целых числах».
2) Кострикин А.И. «Введение в алгебру».
3) Куликов А.Я. «Алгебра и теория чисел».
4) Деза Е.И., Котова А.В. «Сборник задач по теории чисел».
5) Бухштаб А.А. «Теория чисел».






