Разреженные матрицы
При решении широкого круга прикладных проблем, например, при численном решении краевых задач для дифференциальных уравнений в частных производных (в частности, при использовании метода конечных элементов), возникают матрицы значительного порядка, большинство элементов которых равны нулю. Очевидно, что обычное хранение таких матриц приводит к неэффективному использованию памяти компьютера и соответственно к снижению быстродействия вычислений. В системе MATLAB данная проблема преодолевается введением для таких матриц специальных структур данных, называемых разреженными матрицами. Для создания массива, в котором хранится разреженная матрица, используется функция sparse:
>> A=[0 1 0 0; 0 0 1 0; 0 0 0 1; -4 0 0 0]
A =
0 1 0 0
0 0 1 0
0 0 0 1
-4 0 0 0
>> S=sparse (A)
S =
(4, 1) -4
(1, 2) 1
(2, 3) 1
(3, 4) 1
>> whos S
Name Size Bytes Class Attributes
S 4x4 104 double sparse
>> whos A
Name Size Bytes Class Attributes
A 4x4 108 double
Приведённый пример демонстрирует, что функция sparse размещает в памяти компьютера только лишь индексы ненулевых элементов и их значения, при этом матрица S является переменной типа sparse array, занимает в памяти меньше места, чем исходная матрица A.
Обратное преобразование разреженной матрицы в обычную матрицу производится функцией full:
>> full (S)
ans =
0 1 0 0
0 0 1 0
0 0 0 1
-4 0 0 0
В заключение отметим, что в системе MATLAB для операций с разреженными матрицами имеется большое количество функций.
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Нелинейные уравнения подразделяются на два класса: алгебраические и трансцендентные.
Класс алгебраических функций.
Функция называется алгебраической, если для вычисления значения функции по заданному значению аргумента нужно выполнить арифметические операции и возведение в степень с рациональным показателем. (Операция извлечения корня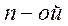 
степени может быть представлена как операция возведения в степень с показателем 
.)
Алгебраическая функция называется рациональной относительно переменной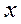 
, если над 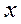не производится никаких других действий, кроме сложения, вычитания, умножения, деления и возведения в целую степень.
Например:
, 
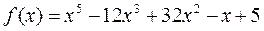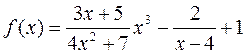
Если в рациональную функцию переменная 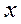не входит в качестве делителя или в выражение, являющееся делителем, то такая функция называется целой рациональной.
Например, следующие функции:
,
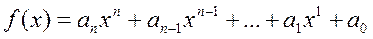где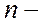 
любое целое число, 
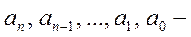любые действительные числа,
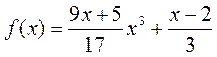
Если в рациональной функции хотя бы один раз встречается деление на переменную 
или переменная 
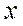входит в выражение, являющееся делителем, то такая функция называется дробно - рациональной.
Например,
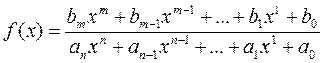
где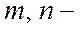 
любые целые числа, 
, 
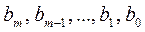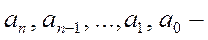любые действительные числа.
Функция называется иррациональной, если для вычисления функции помимо четырех арифметических действий надо выполнить извлечение корня из выражений, содержащих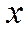 
.
Так, функция
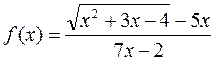
является иррациональной, а функция
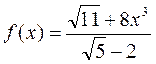
иррациональной не является, так как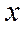 
не находится под знаком радикала.
Класс трансцендентных функций.
К трансцендентным функциям относятся все неалгебраические функции – показательная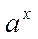 
, логарифмическая 
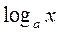, тригонометрические 
, 
, 
, 
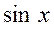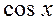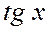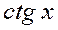; обратные тригонометрические 
, 
, 
, 
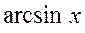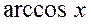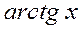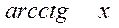, специальные функции уравнений математической физики,…
Например,
, 
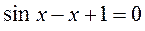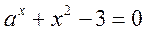
Решение уравнения с одним неизвестным заключается в отыскании корней, т.е. тех значений 
, которые обращают уравнение в тождество. Корни уравнения могут быть вещественными и комплексными.
Найти точные значения корней уравнения можно только в исключительных случаях, как правило, когда существует какая-либо простая формула для вычисления корней.
Отделение корней
Процесс нахождения приближенных значений корней уравнений разбивается на два этапа: 1) отделение корней, 2) уточнение корней до заданной точности.
Корень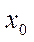 
уравнения 
считается отделенным на отрезке 
, если на этом отрезке уравнение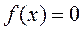 
не имеет других корней.
Отделить корни – это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень. Отделение корней можно произвести двумя методами – графическим и аналитическим.
