Законы распределения дискретных случайных величин
Биномиальное распределение
Дискретная случайная величина X имеет биномиальное распределение B(n,p) (или распределена по биномиальному закону), если она принимает значения 0, 1, 2, …, n, с соответствующими вероятностями:
Иначе говоря, k – это количество удачных исходов в n независимых экспериментах, а p – это вероятность удачного исхода в единичном эксперименте.
Математическое ожидание и дисперсия вычисляются по следующим формулам:
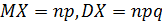
Сравним графики функций вероятности при разных значениях параметрах:
1. Постоянное n, p меняется;
2. Постоянное p, n меняется.
Если 
, то мы получаем распределение Бернулли.
При стремлении n к бесконечности биномиальное распределение приближается к нормальному.
Задача:
15
Формула: 
Распределение Пуассона
Дискретная случайная величина X имеет распределение Пуассона P(
(или распределена по закону Пуассона) с параметром 
, если она принимает бесконечное, но счетное число значений: 0, 1, 2, …, m, …, с соответствующими вероятностями:
Распределение Пуассона моделирует случайную величину, представляющую собой число событий k, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Математическое ожидание и дисперсия вычисляются очень просто:
Сравним графики функций вероятности при разных значениях λ:
Распределение Пуассона является предельным для биномиального закона, когда число испытаний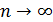 
, а вероятность события 
, при условии, что произведение 
- постоянная величина. При этих условиях (т. е. при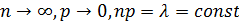 
) величина 
, определяемая по формуле Бернулли, стремится к вероятности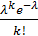 
, определяемой по закону Пуассона.
Поэтому закон распределения Пуассона является хорошим приближением биномиального закона в случае, когда число опытов велико, а вероятность успеха в каждом из них мала. В связи с этим закон распределения Пуассона называют часто законом редких событий. Этот закон распределения используется в теории массового обслуживания.
Задача:
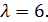
Формула: 
.
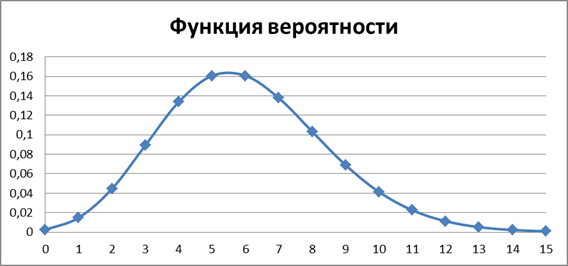
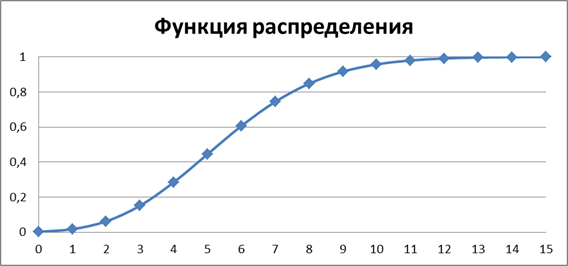
Геометрическое распределение
Дискретная случайная величина X имеет геометрическое распределение G(p), если она принимает бесконечное, но счетное число значений: 0, 1, 2, …, m, …, с соответствующими вероятностями:
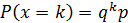, где 
.
Геометрическое распределение – распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».
Математическое ожидание и дисперсия вычисляются по следующим формулам:
Сравним графики функций вероятности при разных значениях λ:
Задача:
Формула: 
0,(3)
