Анализ резистивных цепей постоянного тока
Для схемы, соответствующей номеру варианта, выполнить:
1. Записать уравнения по законам Кирхгофа. Решив полученную систему уравнений, определить токи и напряжения ветвей.
2. Составить узловые уравнения цепи в матричной форме. Решив составленные уравнения, рассчитать токи во всех ветвях исходной цепи.
3. Составить расширенные узловые уравнения.
4. Результаты расчетов свести в таблицу.
5. Рассчитать ток в ветви с резистором  методом эквивалентного генератора.
методом эквивалентного генератора.
6. Определить, при каком сопротивлении резистора  в нем выделяется максимальная мощность.
в нем выделяется максимальная мощность.
7. Построить графики зависимостей тока, напряжения и мощности, выделяемой в резисторе  при изменении сопротивления от
при изменении сопротивления от  до
до 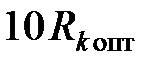 .
.
Примечание: коэффициент усиления управляемого источника  принять равным последней цифре номера зачетной книжки. Цифре 0 соответствует
принять равным последней цифре номера зачетной книжки. Цифре 0 соответствует  . Параметр источника тока, управляемого током (ИТУН)
. Параметр источника тока, управляемого током (ИТУН)  (
( – последняя цифра номера зачетной книжки).
– последняя цифра номера зачетной книжки).
Таблица 1
| Вар. | Рис. | R1 | R2 | R3 | R4 | R5 | R6 | Rk | E 1 | E 2 | E 3 | J 1 | J 2 | J 3 |
| Ом | В | А | ||||||||||||
| 1.2 | — | — | 0,5 | — | 0,8 | |||||||||
| 1.15 | 19,5 | 7,5 | 13,5 | 10,5 | — | — | — | 0,8 | ||||||
| 1.1 | 19,5 | 7,5 | 16,5 | 22,5 | — | — | 0,8 | — | ||||||
| 1.11 | 52,5 | — | 0.5 | — | — | |||||||||
| 1.17 | 7,5 | — | 16,5 | 52,5 | — | — | 0,5 | |||||||
| 1.3 | 19,5 | 13,5 | 7,5 | — | 16,2 | — | 0,4 | |||||||
| 1.7 | 67,5 | 10,2 | — | — | 0,04 | — | ||||||||
| 1.2 | 7,5 | 10,5 | — | — | — | |||||||||
| 1.8 | 82,5 | — | 25,5 | 22,5 | — | 0,1 | — | |||||||
| 1.1 | — | — | 0.1 | — | ||||||||||
| 1.14 | — | — | — | 0,5 | ||||||||||
| 1.18 | — | — | 22,5 | — | 0,3 | 0,4 | ||||||||
| 1.12 | 22,5 | 1,35 | 10,5 | — | — | — | 0,2 | 0,3 | — | |||||
| 1.14 | 13,5 | — | — | — | ||||||||||
| 1.6 | 7,5 | 10,5 | 22,5 | — | — | 37,5 | — | 0,5 | — | |||||
| 1.19 | 22,5 | — | — | — | ||||||||||
| Продолжение Таблицы 1 | ||||||||||||||
| 1.2 | — | — | — | 0,5 | ||||||||||
| 1.15 | — | — | — | 0,4 | ||||||||||
| 1.1 | 6,5 | 2,5 | 5,5 | 7,5 | — | — | 0,4 | — | ||||||
| 1.16 | 6,5 | — | — | 7,5 | — | 0,4 | ||||||||
| 1.11 | 17,5 | — | 0.4 | — | — | |||||||||
| 1.2 | 7,5 | 10,5 | — | — | 0,5 | — | 0,5 | |||||||
| 1.15 | 26,25 | — | — | — | ||||||||||
| 1.1 | — | — | — | |||||||||||
| 1.17 | 2,5 | — | 8,2 | 17,5 | — | — | 0,2 | |||||||
| 1.3 | 6,5 | 4,5 | 2,5 | — | 6,7 | — | 0,2 | — | ||||||
| 1.7 | 22,5 | 4,7 | — | — | 0,02 | 0,2 | — | |||||||
| 1.20 | 2,5 | 3,5 | — | — | — | 0,15 | ||||||||
| 1.8 | 27,5 | — | 6,5 | 7,5 | — | 0,15 | — | |||||||
| 1.10 | 8,1 | — | 0,08 | — | — | |||||||||
| 1.9 | 3,5 | 4,5 | 7,5 | — | — | 0,5 | — | |||||||
| 1.18 | — | 7,5 | — | — | 0,2 | 0,5 | ||||||||
| 1.4 | 52,5 | 22,5 | — | — | — | 0,4 | 0,3 | |||||||
| 1.13 | 10,5 | 8,25 | — | — | — | 0,4 | ||||||||
| 1.5 | 16,5 | 7,5 | 10,5 | 25,5 | — | — | — | |||||||
| 1.12 | 7,5 | 4,5 | 3,5 | — | — | — | 0,4 | 0,2 | — | |||||
| 1.9 | 10,5 | 13,5 | 22,5 | — | — | — | ||||||||
| 1.6 | 2,5 | 3,5 | 7,5 | — | — | 12,5 | — | 0,3 | — | |||||
| 1.19 | 2,5 | 3,5 | 7,5 | — | 0,2 | — | — | |||||||
| 1.4 | 17,5 | 7,5 | — | 6,5 | — | — | 0,2 | 0,4 | ||||||
| 1.13 | 3,5 | 2,75 | — | — | — | 0,4 | ||||||||
| 1.5 | 7,5 | 3,5 | 10,5 | — | — | — | ||||||||
| 1.16 | — | — | — | 0,5 | ||||||||||
| 1.11 | — | 0.8 | — | — | ||||||||||
| 1.17 | — | — | — | |||||||||||
| 1.3 | — | — | 0,5 | — | ||||||||||
| 1.7 | — | — | 0,5 | 0,2 | — | |||||||||
| 1.20 | — | — | — | 0,5 | ||||||||||
| 1.8 | — | — | 0,04 | — | ||||||||||
| 1.14 | — | — | — | 0,25 | ||||||||||
| 1.10 | — | 0,05 | — | — | ||||||||||
| 1.9 | — | — | — | |||||||||||
| 1.18 | — | — | — | 0,5 | ||||||||||
| 1.12 | — | — | — | 0,5 | 0,5 | — | ||||||||
| 1.4 | — | — | — | 0,5 | 0,1 | |||||||||
| 1.13 | — | — | — | 0,5 | 1,5 | |||||||||
| 1.5 | 16,6 | — | 0,2 | — | — | |||||||||
| 1.20 | 12,5 | 17,5 | — | — | — | 0,5 | ||||||||
| Окончание Таблицы 1 | ||||||||||||||
| 1.6 | — | — | — | 0,5 | — | |||||||||
| 1.19 | — | — | — | |||||||||||
| 1.15 | 32,5 | 12,5 | 22,5 | 17,5 | — | — | — | 0,4 | ||||||
| 1.1 | 32,5 | 12,5 | 27,5 | 37,5 | — | — | 0,4 | — | ||||||
| 1.16 | 32,5 | — | — | 37,5 | — | 0,4 | ||||||||
| 1.11 | — | — | — | 0,5 | ||||||||||
| 1.17 | 12,5 | — | 87,5 | — | — | 0,4 | ||||||||
| 1.3 | 32,5 | 22,5 | 12,5 | — | — | 0,4 | — | |||||||
| 1.7 | — | — | 0,04 | 0,4 | — | |||||||||
| 1.2 | — | — | — | 0,5 | ||||||||||
| 1.8 | — | 34,5 | 37,5 | — | 0,14 | — | ||||||||
| 1.10 | — | 0,14 | — | — | ||||||||||
| 1.9 | 17,5 | 22,5 | 37,5 | — | — | 0,8 | — | |||||||
| 1.18 | — | 32,5 | — | — | 0,25 | 0,8 | ||||||||
| 1.12 | 37,5 | 22,5 | 17,5 | — | — | — | 0,2 | 0,25 | — | |||||
| 1.4 | 87,5 | 37,5 | — | — | — | 0,4 | 0,8 | |||||||
| 1.13 | 17,5 | 13,75 | — | — | — | 0,25 | ||||||||
| 1.5 | 27,5 | 12,5 | 17,5 | 32,5 | — | — | — | |||||||
| 1.14 | 22,5 | — | — | — | 0,8 | |||||||||
| 1.6 | 12,5 | 17,5 | 37,5 | — | — | 62,5 | — | 0,1 | — | |||||
| 1.19 | 12,5 | 17,5 | 37,5 | — | 0,6 | — | — | |||||||
| 1.2 | 37,5 | 52,5 | — | — | 0,6 | — | 0,6 | |||||||
| 1.15 | — | — | — | |||||||||||
| 1.1 | — | — | — | |||||||||||
| 1.16 | — | — | — | 0,6 | ||||||||||
| 1.11 | — | 0.8 | — | — | ||||||||||
| 1.17 | — | — | — | |||||||||||
| 1.3 | — | 8,2 | — | 0,2 | — | |||||||||
| 1.7 | — | — | 0,2 | 0,3 | — | |||||||||
| 1.20 | — | — | — | 0,6 | ||||||||||
| 1.8 | — | — | 0,05 | — | ||||||||||
| 1.10 | — | 0,1 | — | — | ||||||||||
| 1.9 | — | — | 0,5 | — | ||||||||||
| 1.18 | — | — | — | 0,6 | 0,25 | |||||||||
| 1.12 | — | — | — | 0,2 | 0,5 | — | ||||||||
| 1.4 | — | — | — | 0,5 | 0,2 | |||||||||
| 1.13 | 5,5 | — | — | — | 0,25 | |||||||||
| 1.5 | 4,5 | — | 0,5 | — | — | |||||||||
| 1.14 | — | — | — | 0,5 | ||||||||||
| 1.6 | — | — | ||||||||||||
| 1.19 | — | — | — | — | ||||||||||
| 1.16 | 19,5 | — | — | 22,5 | — | 0,5 |
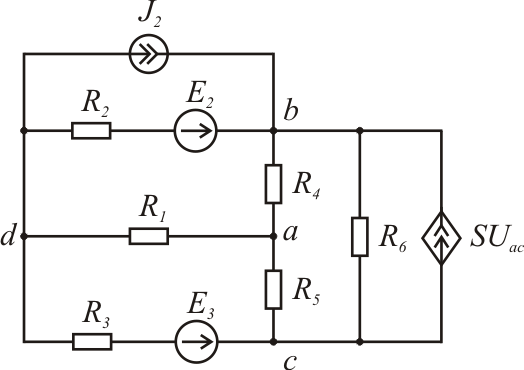 Рис. 1.1
Рис. 1.1
|  Рис. 1.2
Рис. 1.2
|
 Рис. 1.3
Рис. 1.3
|
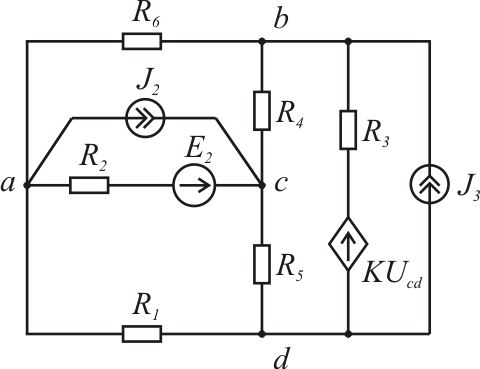 Рис. 1.4
Рис. 1.4
|
 Рис. 1.5
Рис. 1.5
|
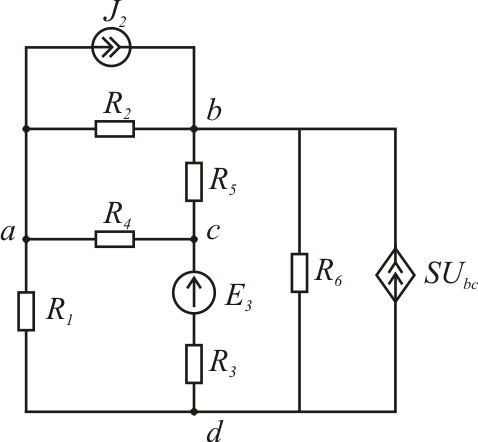 Рис. 1.6
Рис. 1.6
|
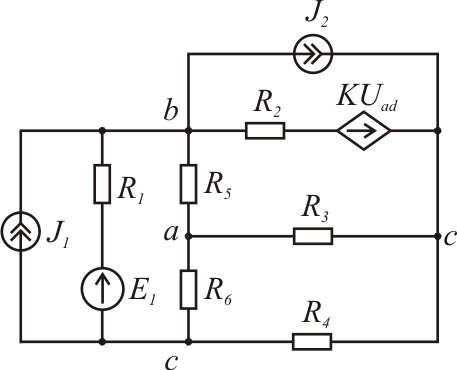 Рис. 1.7
Рис. 1.7
|  Рис. 1.8
Рис. 1.8
|
 Рис. 1.9
Рис. 1.9
|
 Рис. 1.10
Рис. 1.10
|
 Рис. 1.11
Рис. 1.11
|
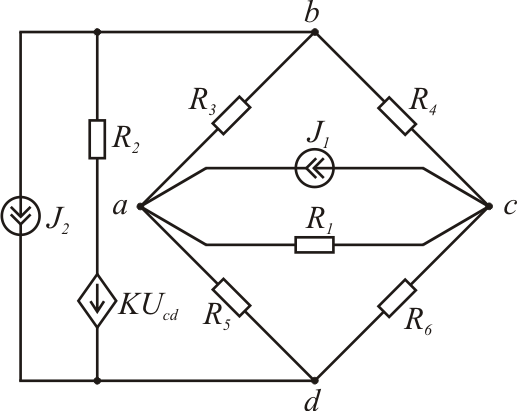 Рис. 1.12
Рис. 1.12
|
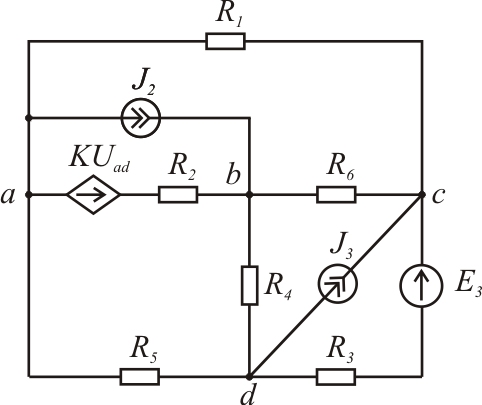 Рис. 1.13
Рис. 1.13
|
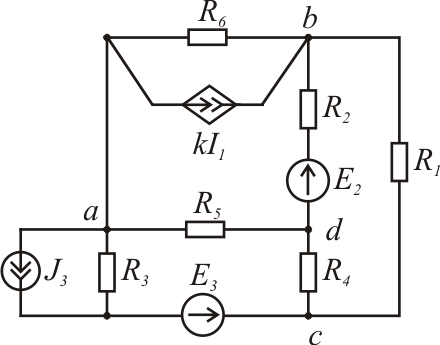 Рис. 1.14
Рис. 1.14
|
 Рис. 1.15
Рис. 1.15
|
 Рис. 1.16
Рис. 1.16
|
 Рис. 1.17
Рис. 1.17
|
 Рис. 1.18
Рис. 1.18
|
 Рис. 1.19
Рис. 1.19
| 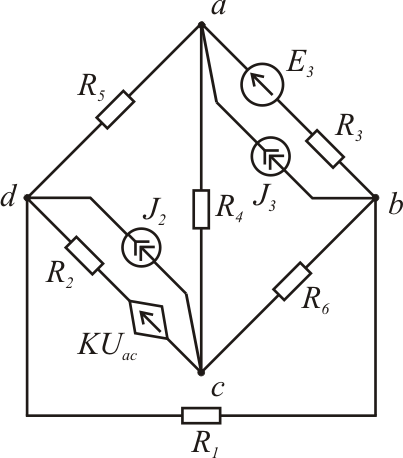 Рис. 1.20
Рис. 1.20
|
Рекомендации по выполнению расчетного задания
1. Последовательное соединение резистора и источника напряжения следует рассматривать как одну ветвь.
2. Схемы для всех вариантов имеют примерно одинаковую сложность. Для всех схем достаточно составить три уравнения по первому закону Кирхгофа и три – по второму.
3. п. 3 расчетного задания (составление расширенных узловых уравнений) студентам ЗФ выполнять не нужно.
4. При составлении уравнений по методу узловых напряжений источники напряжения следует преобразовать в эквивалентные источники тока.
5. При выполнении п. 5 (расчет методом эквивалентного генератора) следует помнить, что в цепи с управляемыми источниками входное сопротивление можно найти только как отношение напряжения холостого хода к току короткого замыкания. Напряжение холостого хода можно найти из системы узловых уравнений, полагая проводимость первого резистора равной нулю: 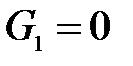 . Ток короткого замыкания легко найти, решив систему уравнений по законам Кирхгофа (п. 1 расчетного задания). В этой системе следует принять
. Ток короткого замыкания легко найти, решив систему уравнений по законам Кирхгофа (п. 1 расчетного задания). В этой системе следует принять 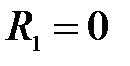 . В этом случае ток короткого замыкания
. В этом случае ток короткого замыкания  .
.
Пример выполнения п. 1 и 2 расчетного задания № 1
1. Записать систему уравнений по законам Кирхгофа для цепи, показанной на рис. 1.
| R |
| R |
| R |
| J |
| R |
| R |
| E |
| E |
| U |
| S |
| U |
Рис. 1
1.1. Произвольно выбираем направление токов в ветвях исходной цепи.
Запишем уравнения по первому закону Кирхгофа для узлов 1, 2, 3.
Токи, направленные от узла, записываем со знаком «+». Токи, направленные к узлу, записываем со знаком «-».
Для узла 1:

Для узла 2:

Для узла 3:
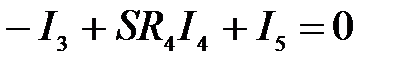 .
.
Учитываем, что  (напряжение на четвёртом резисторе определяем по закону Ома:
(напряжение на четвёртом резисторе определяем по закону Ома:  ).
).
В качестве контуров удобно выбирать внутренние ячейки. Направление обхода контуров выберем совпадающим с направлением часовой стрелки.
Уравнения по второму закону Кирхгофа:
Контур 1:

Контур 2:

Таким образом, получаем следующую систему уравнений:


 .
.

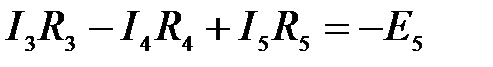
В матричной форме:
 .
.
Для решения уравнений необходимо использовать математические пакеты (MathCAD или MatLab). Решая систему уравнений, получим вектор токов ветвей. Напряжения ветвей найдем с помощью закона Ома: 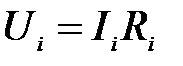 .
.
2. Записать систему уравнений по методу узловых напряжений для схемы, показанной на рис. 1.
Решение. Преобразуем цепь на рис. 1 к виду, удобному для анализа методом узловых напряжений. Последовательную ветвь источник напряжения - резистор преобразуем в параллельную ветвь с источником тока (рис. 2). Источник тока, управляемый напряжением, не требует отдельного преобразования.
Рис. 2
Выберем в качестве базисного узел 0.
Относительно базисного узла определяем направление узловых напряжений  ,
,  ,
, 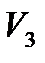 . Эти напряжения в узлах цепи, отсчитанные относительно базисного узла, называют узловыми напряжениями.
. Эти напряжения в узлах цепи, отсчитанные относительно базисного узла, называют узловыми напряжениями.
При составлении уравнений по методу узловых напряжений предварительно записывать уравнения по первому закону Кирхгофа не нужно!
Алгоритм формирования узловых уравнений рассмотрен в п. 3.2 учебного пособия. Последовательно просматриваем ветви схемы. Если k-я ветвь включена между узлами i и j, то проводимость этой ветви войдёт в элементы матрицы узловых проводимостей, которые находятся на пересечении строк и столбцов с номерами i и j. На главной диагонали все проводимости записываем со знаком «+», вне главной диагонали со знаком «-». Процедура составления уравнений заканчивается, когда рассмотрены все ветви.
Матрица узловых проводимостей цепи, показанной на рис. 2:
 .
.
Вектор узловых напряжений:
 .
.
Система уравнений по методу узловых напряжений:
 .
.
Токи ветвей найдем из соотношений:
 ;
;
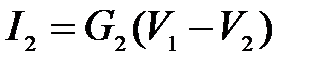 ;
;
 .
.
Для того чтобы найти токи  и
и  , необходимо вернуться к первоначальной схеме и записать уравнения по второму закону Кирхгофа для ветвей с источниками напряжения.
, необходимо вернуться к первоначальной схеме и записать уравнения по второму закону Кирхгофа для ветвей с источниками напряжения.
 , ,
| 
| ||||||||||||
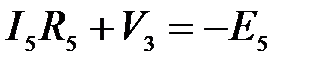

| 
|






