а) 
, где а, в, с – стороны треугольника;
б) радиус описанной окружности равен отношению стороны треугольника к удвоенному синусу противолежащего угла 
;
в) для равностороннего треугольника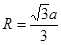 
;
г) для прямоугольного треугольника 
, где с – гипотенуза треугольника;
д)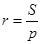 
, где S – площадь треугольника, р – его полупериметр;
е) для равностороннего треугольника 
;
ж) для прямоугольного треугольника 
, где а, в – катеты, с – гипотенуза.
Свойство треугольников, на которые разбивается трапеция диагоналями
Диагонали трапеции разбивают её на четыре треугольника, причём, треугольники, прилежащие к основаниям трапеции подобны, а прилежащие к боковым сторонам равновелики.
Особое свойство трапеции
В любой трапеции четыре точки лежат на одной прямой: середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон.
Свойства трапеции, в которую можно вписать окружность
а) боковая сторона трапеции видна из центра окружности под прямым углом;
б) радиус окружности есть среднее геометрическое отрезков, на которые точка касания делит боковую сторону;
в) если трапеция при этом равнобокая, то боковая сторона равна средней линии.
Соотношения между сторонами и диагоналями параллелограмма
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Свойство треугольников, на которые параллелограмм делится диагоналями
а) каждая диагональ параллелограмма делит его на два равных треугольника;
б) две диагонали параллелограмма делят его на четыре равновеликих треугольника.
Свойства угла между высотами параллелограмма
Высоты параллелограмма, опущенные из одной вершины, образуют угол, равный углу параллелограмма при соседней вершине.
Свойства биссектрис параллелограмма
Биссектрисы смежных углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллелограмма параллельны или лежат на одной прямой.
Свойство окружности, вписанной в четырехугольник и описанной около четырехугольника
а) в четырехугольник можно вписать окружность тогда и только тогда, когда суммы противолежащих сторон равны;
б) около четырехугольника можно описать окружность тогда и только тогда, когда сумма противолежащих углов четырехугольника равна 180 градусов.
Свойства центрального и вписанного угла окружности
Центральный угол окружности равен дуге, на которую он опирается, вписанный угол окружности равен половине дуги, на которую он опирается.
