Перечень практических работ по математике. 2 курс, (для специальностей: 134702, 080110).
1. Вычисление пределов функций.
2. Определение непрерывности функций. Классификация точек разрыва.
3. Нахождение производных функций первого порядка.
4. Нахождение производных функций высших порядков.
5. Нахождение точек перегиба и направлений выпуклости, асимптот графика функции
6. Исследование функции по общей схеме.
7. Нахождение неопределенного интеграла методом введения новой переменной.
8. Нахождение неопределенных интегралов методом интегрирования «по частям».
9. Приближенные методы вычисления определенных интегралов.
10. Решение несложных задач на определение различных величин с помощью определенных интегралов.
Практическая работа № 1
по дисциплине «Математика»
по теме: «Вычисление пределов функций»
для специальностей 134702, 080110. 2 курс.
Вариант 1.
Найти пределы:
1) lim (3х³ - 2х² + х – 5)
х → - 1
2) lim 
х → 4
3) lim 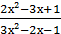
х → 1
4) lim 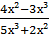
х → 0
5) lim 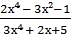
х → ∞
6) lim 
х → ∞
7) lim 
х → ∞
8) lim 
х → ∞
9) lim 
х → ∞
10)lim 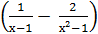
х → 1
Практическая работа № 1
по дисциплине «Математика»
по теме: «Вычисление пределов функций» для специальностей 134702, 080110. 2 курс.
Вариант 2.
Найти пределы:
1) lim (5х³ + 4х – 4х + 2)
х → - 1
2) lim 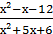
х → - 3
3) lim 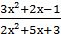
х →-1
4) lim 
х → 0
5) lim 
х → ∞
6) lim 
х → ∞
7) lim 
х → ∞
8) lim 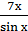
х → 0
9) lim 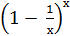
х →∞
10)lim 
х → 2
Практическая работа № 1
по дисциплине «Математика»
по теме: «Вычисление пределов функций»
для специальностей 134702, 080110. 2 курс.
Вариант 3. Найти пределы:
1) lim (4х³ - 3х² + х + 7)
х → - 1
2) lim 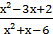
х → 2
3) lim 
х → -1
4) lim 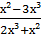
х → 0
5) lim 
х → ∞
6) lim 
х → ∞
7) lim 
х → ∞
8) lim 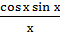
х → 0
9) lim 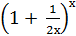
х → ∞
10)lim 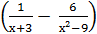
х → -3
Практическая работа № 1
по дисциплине «Математика»
по теме: «Вычисление пределов функций»
для специальностей 134702, 080110. 2 курс.
Вариант 4. Найти пределы:
1) lim (2х³ + х² - 3х – 4)
х → -2
2) lim 
х → 3
3) lim 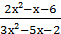
х → 2
4) lim 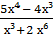
х → 0
5) lim 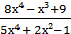
х → ∞
6) lim 
х → ∞
7) lim 
х → ∞
8) lim 
х → 0
9) lim 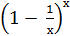
х → ∞
10) lim 
х → 5
Практическая работа № 2
по дисциплине «Математика»
по теме: «Определение непрерывности функции,
Точек разрыва функции»для специальностей134702, 080110. 2 курс.
Вариант 1.
1. Определить непрерывность функции в указанных точках:
а) у = 2х – 4; х = 3;
б) у = 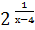 , х = 2, х = 4;
, х = 2, х = 4;
в) у = 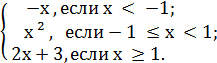
Установить характер точек разрыва.
2. Изобразите на чертеже графики функций.
Практическая работа № 2
по дисциплине «Математика»
по теме: «Определение непрерывности функции,
точек разрыва функции»
для специальностей 134702, 080110. 2 курс.
Вариант 2.
1. Определить непрерывность функции в указанных точках:
а) у = 5х – 4, х = 1;
б) у =  , х = - 1, х = 1;
, х = - 1, х = 1;
в) у = 
Установить характер точек разрыва.
2. Изобразите на чертеже графики функций.
Практическая работа № 2
по дисциплине «Математика»
по теме: «Определение непрерывности функции,
точек разрыва функции»
для специальностей 134702, 080110. 2 курс.
Вариант 3.
1. Определить непрерывность функции в указанных точках:
а) у = -х + 3, х = 5;
б) у =  , х = - 2, х = 0;
, х = - 2, х = 0;
в) у = 
Установить характер точек разрыва.
2.Изобразите на чертеже графики функций.
Практическая работа № 2
по дисциплине «Математика»
по теме: «Определение непрерывности функции,
точек разрыва функции»
для специальностей 134702, 080110. 2 курс.
Вариант 4.
1. Определить непрерывность функции в указанных точках:
а) у = 4х – 3, х = 1;
б) у = 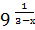 , х = 1, х = 3;
, х = 1, х = 3;
в) у = 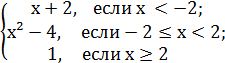
Установить характер точек разрыва.
2.Изобразите на чертеже графики функций.
Составила преподаватель: Чуфенёва Н.И.
Практическая работа № 3
по дисциплине «Математика»
по теме: Нахождение производной сложной, обратных функций»
для специальностей 134702, 080110. 2 курс.
Вариант 1.
Найти производные первого порядка следующих функций:
1) у = 3х⁵;
2) у = 4х-7;
3) у = 2 · 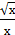 ;
;
4) у =  +
+ 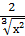 -
- 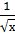 + 1;
+ 1;
5) у = (2х – 1) (х² + 3х – 4);
6) у =  ;
;
7) у = (х³ - 4х² + 1)6;
8) у = 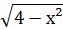 ;
;
9) у = ln  ;
;
10) у = х² +  ;
;
11) у =  + ln х;
+ ln х;
12) у = 4 ·  ;
;
13) у = tg  ;
;
14) у =  ;
;
15)у =  · ln(2х + 5) -
· ln(2х + 5) -  в точке х0 = -1.
в точке х0 = -1.
Практическая работа № 3
по дисциплине «Математика»
по теме «Нахождение производной сложной, обратных функций»
для специальностей 134702, 080110. 2 курс.
Вариант 2.
Найти производные первого порядка следующих функций:
1) у = 4х⁶;
2) у = 5х-3;
3) у = 3·  ;
;
4) у =  -
-  +
+ 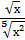 - 2;
- 2;
5) у = (х-4) (3х² + 2х +7);
6) у =  ;
;
7) у = (2х⁴ - 3х + 1)7;
8) у =  ;
;
9) у = ln  ;
;
10) у = х³ - соsх;
11) у =  – ln 3х;
– ln 3х;
12) у = 8 · 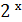 ;
;
13) у = сtg 2х;
14) у = 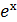 ·
· 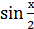 ;
;
15) у =  +
+  в точке х = 1
в точке х = 1
Практическая работа № 3
по дисциплине «Математика»
по теме: «Нахождение производной сложной, обратных функций»
для специальностей 134702, 080110. 2 курс.
Вариант 3.
Найти производные первого порядка следующих функций:
1) у = 6х⁵;
2) у = 3х-4;
3) у = 2 ·  ;
;
4) у = 5  -
-  +
+  - 7;
- 7;
5) у = (4х + 3) (х² - 3х + 1);
6) у = 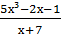 ;
;
7) у = (7х² - 8х + 2)7;
8) у = 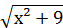 ;
;
9) у = 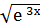 ;
;
10) у = ln  ;
;
11) у = 7 ·  ;
;
12) у = соs² 3х;
13) у = tg  + ln х;
+ ln х;
14) у =  ·
·  );
);
15) у =  ;
;
Практическая работа № 3по дисциплине «Математика»по теме: «Нахождение производной сложной, обратных функций»для специальностей 134702, 080110. 2 курс.
Вариант 4.
Найти производные первого порядка следующих функций»
1) у = 7х³;
2) у = 5х-8;
3) у = 3 ·  ;
;
4) у = 2  +
+  -
-  - 1;
- 1;
5) у = (7х – 2) (4х² - х+ 3);
6) у =  ;
;
7) у = (4х² + 5х – 7)8;
8) у = 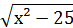 ;
;
9) у =  ;
;
10) у = ln  ;
;
11) у = 9 ·  ;
;
12) у =  ;
;
13) у = сtg  + eх;
+ eх;
14) у = 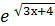 · соs (х -
· соs (х -  );
);
15) у = 7 (х-1)3 –  +
+  в точке х = 1.
в точке х = 1.
Составила преподаватель: Чуфенёва Н.И.
Практическая работа № 4
по дисциплине «Математика»
по теме: «Нахождение производных функций высших порядков»
для специальностей 134702, 080110. 2 курс.
Вариант 1.
1. Вопросы для повторения:
1) Дайте определение производной второго порядка.
2) В чем заключается механический смысл производной второго порядка?
3) Дайте определение производной третьего порядка.
4) Дайте определение производной n-го порядка.
2. Найти производную второго порядка функции (1 -5).
Найти производную третьего порядка для функции (6 – 10).
1. у = 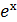 +
+  ;
;
2. у = х5 ln х;
3. у = 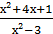 ;
;
4. у = 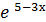 ;
;
5. у = ln (2 – 3х);
6. у = соs (7 – 6х);
7. у = 3  –
– 
8. у = х³  ;
;
9. у =  ;
;
10. у = аrсsin  .
.
Практическая работа № 4
по дисциплине «Математика»
по теме: «Нахождение производных функций высших порядков» для специальностей 134702, 080110. 2 курс.
Вариант 2.
1. Вопросы для повторения:
1) Дайте определение производной второго порядка.
2) В чем заключается механический смысл производной второго порядка?
3) Дайте определение производной третьего порядка.
4) Дайте определение производной n-го порядка.
2. Найти производную второго порядка функции (1-5).
Найти производную третьего порядка для функции (6 – 10)
1. у = соs х – ln х;
2. у = х³ tgх;
3. у = 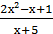 ;
;
4. у = 
5. у = ln (4х + 1);
6. у = sin( - х);
- х);
7. у = 4  -
-  ;
;
8. у = соs³ 3х;
9. у = х² 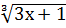 ;
;
10. у = аrсоs (х + 2).
Практическая работа № 4
по дисциплине «Математика»
по теме: « Нахождение производных функций высших порядков» для специальностей 134702, 080110. 2 курс.
Вариант 3.
1. Вопросы для повторения:
1) Дайте определение производной второго порядка.
2) В чем заключается механический смысл производной второго порядка?
3) Дайте определение производной третьего порядка.
4) Дайте определение производной n-го порядка.
2.Найдите производную второго порядка функции (1- 5).
Найдите производную третьего порядка функции (6-10).
1. у = соsх +  ;
;
2. у = х⁴ lnх;
3. у = 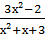 ;
;
4. у =  ;
;
5. у = ln(4 + 5х);
6. у = sin (0,2х – 5);
7. у = 2 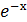 +
+  ;
;
8. у = lnх ·  ;
;
9. у = соs² 4х;
10. у = аrсtg х²
Практическая работа № 4
по дисциплине «Математика»
по теме: «Нахождение производных функций высших порядков» для специальностей 134702, 080110. 2 курс.
Вариант 4.
1. Вопросы для повторения:
1) Дайте определение производной второго порядка.
2) В чем заключается механический смысл производной второго порядка?
3) Дайте определение производной третьего порядка.
4) Дайте определение производной n-го порядка.
2. Найдите производную второго порядка функции (1-5).
Найдите производную третьего порядка функции (6-10).
1. у = lnх – sinх;
2. у = х⁴ 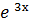 ;
;
3. у = 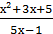 ;
;
4. у = tg 4х;
5. у =  ;
;
6. у = соs( -х);
-х);
7. у = 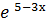 +
+ 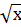 ;
;
8. у = 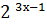 ·
·  ;
;
9. у = sin⁴х;
10. у = аrсtg х³.
Составила преподаватель Чуфенёва Н.И
Практическая работа № 5
по дисциплине «Математика»
по теме: «Нахождение точек перегиба и направлений выпуклости, асимптот графика функции»
для специальностей 134702, 080110. 2 курс.
Вариант 1.
1. Найти точки перегиба и направления выпуклости графика функции:
1) у = 3х – 4;
2) у = 2х² - 3х + 1;
3) у = - х³ + 4х + 3;
4) у = х⁴ - 2х ²+1;
5) у = 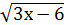 ;
;
6) у =  ;
;
7) у = 
2. Найти асимптоты графика функции:
1) у = х² + 2х + 5;
2) у = 3х³ - 2х² - 4;
3) у = 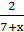 ;
;
4) у =  ;
;
5) у =  .
.
Практическая работа № 5
по дисциплине «Математика»
по теме: «Нахождение точек перегиба и направлений выпуклости, асимптот графика функции»
для специальностей 134702, 080110. 2 курс.
Вариант 2.
1. Найти точки перегиба и направления выпуклости графика функции:
1) у = -х + 3;
2) у = 3х² - х + 5;
3) у = х³ - 3х² - 2;
4) у = -х⁴ + 4х² - 3;
5) у =  ;
;
6) у = 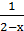 ;
;
7) у =  .
.
2. Найти асимптоты графика функции:
1) у = 2х² + х – 1;
2) у = 2х³ - х² + 3;
3) у =  ;
;
4) у =  ;
;
5) у =  .
.
Практическая работа № 5
по дисциплине «Математика»
по теме: «Нахождение точек перегиба и направлений выпуклости графика функции»
для специальностей 134702, 080110. 2 курс.
Вариант 3.
1. Найти точки перегиба и направления выпуклости графика функции:
1) у = 4х – 5;
2) у = - х² + 2х + 3;
3) у = 2х³ + 3х² - 4;
4) у = 2х⁴ - 4х² + 1;
5) у =  ;
;
6) у = 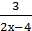 ;
;
7) у =  .
.
2. Найти асимптоты графика функции:
1) у = 3х² - 6х + 2;
2) у = х³ + 3х – 4;
3) у =  ;
;
4) у = 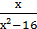 ;
;
5) у = 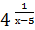
Практическая работа № 5
по дисциплине «Математика»
по теме: «Нахождение точек перегиба и направлений выпуклости графика функции»
для специальностей 134702, 080110. 2 курс.
Вариант 4.
1. Найти точки перегиба и направления выпуклости графика функции:
1) у = 7х + 2;
2) у = 2х² - 4х + 1;
3) у = - х³ + 3х² + 2;
4) у = х⁴ + 2х² - 3;
5) у =  ;
;
6) у =  ;
;
7) у =  .
.
2. Найти асимптоты графика функции:
1) у = 4х² - 2х + 7;
2) у = 3х³ + х + 2;
3) у =  ;
;
4) у =  ;
;
5) у = 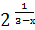 .
.
Составила преподаватель Чуфенёва Н.И.
Практическая работа № 6
по дисциплине «Математика»
по теме: «Исследование функции по общей схеме»
для специальностей 134702, 080110. 2 курс.
Вариант 1.
1. Найти промежутки монотонности и точки экстремумов функции:
1) у = - 2х + 4;
2) у = 3х² - 3х + 1;
3) у = х³ - 3х – 2;
4) у =  ;
;
5) у =  .
.
2. Исследовать функцию и построить график:
1) у = - х² + 2х + 3;
2) у = 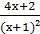 .
.
Практическая работа № 6
по дисциплине «Математика»
по теме: «Исследование функции по общей схеме»
для специальностей 134702, 080110. 2 курс.
Вариант 2.
1. Найти промежутки монотонности и точки экстремумов функции:
1) у = 4х + 1;
2) у = 2х² - 4х + 3;
3) у = - х³ + 6х – 1;
4) у = 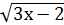 ;
;
5) у = 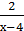 .
.
2. Исследовать функцию и построить график:
1) у = - 2х² + 3х – 1;
2) у = 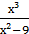 .
.
Практическая работа № 6
по дисциплине «Математика»
по теме: «Исследование функции по общей схеме»
для специальностей 134702, 080110. 2 курс.
Вариант 3.
1. Найти промежутки монотонности и точки экстремумов функции:
1) у = 3х – 4;
2) у = - х² + 2х + 3;
3) у = х³ - 3х² + 2;
4) у =  ;
;
5) у = 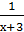 .
.
2. Исследовать функцию и построить график:
1) у = 2х² - 3х + 1;
2) у =  .
.
Практическая работа № 6
по дисциплине «Математика»
по теме: «Исследование функции по общей схеме»
для специальностей 134702, 080110. 2 курс.
Вариант 4.
1. Найти промежутки монотонности и точки экстремумов функции:
1) у = - 7х + 5;
2) у = 2х² + 4х – 3;
3) у = 3х³ - 3х² + 1;
4) у =  ;
;
5) у = 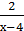 .
.
2. Исследовать функцию и построить график:
1) у = - 3х² + 3х – 2;
2) у =  .
.
Практическая работа № 7
по дисциплине «Математика»
по теме: «Нахождение неопределенного интеграла методом введения новой переменной»
для специальностей 134702, 080110. 2 курс.
Вариант 1.
Найти неопределенные интегралы методом подстановки:
1. ∫ (3х2 + 2)5 · х dх;
2. ∫(2х3 – 1)3 · х2 dх;
3. ∫ 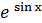 · соsх dх;
· соsх dх;
4. ∫ 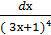 ;
;
5. ∫sin 6хdх;
6. ∫  · хdх;
· хdх;
7. ∫(5х – 4)⁶dх;
8. ∫ 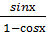 dх;
dх;
9. ∫ соs2х · sinх dх;
10. ∫  ;
;
11. ∫  · х dх;
· х dх;
12. ∫ 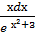 ;
;
13. ∫  · х³dх;
· х³dх;
14. ∫х³· соsх⁴dх;
15. ∫ 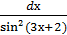
Практическая работа № 7
по дисциплине «Математика»
по теме: «Нахождение неопределенно интеграла методом введения новой переменной»
для специальностей 134702, 080110. 2 курс.
Вариант 2.
Найти неопределенные интегралы методом подстановки:
1. ∫(2х² - 4)⁶ · х dх;
2. ∫(4х³ + 1)⁴ · х² dх;
3. ∫ 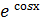 · sinх dх;
· sinх dх;
4. ∫ 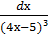 ;
;
5. ∫соs  dх;
dх;
6. ∫ 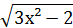 ·х dх;
·х dх;
7. ∫(7х + 5)⁵ dх;
8. ∫  dх;
dх;
9. ∫sin²х · соsх dх;
10. ∫ 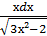 ;
;
11. ∫  · х²dх;
· х²dх;
12. ∫ 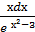 ;
;
13. ∫  ·х³dх;
·х³dх;
14. ∫х⁵· sinх⁶dх;
15. ∫ 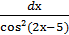
Практическая работа № 7
по дисциплине «Математика»
по теме: «Нахождение неопределенных интегралов методом введения новой переменной»
для специальностей 134702, 080110. 2 курс.
Вариант 3.
Найти неопределенные интегралы методом подстановки:
1. ∫(5х² - 3)⁶·хdх;
2. ∫(3х³ + 2)⁴ · х²dх;
3. ∫  ·хdх;
·хdх;
4. ∫  ;
;
5. ∫sin  dх;
dх;
6. ∫  ·хdх;
·хdх;
7. ∫(3х + 4)⁶dх;
8. ∫ 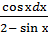 ;
;
9. ∫ 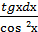 ;
;
10. ∫ 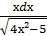 ;
;
11. ∫  ·х²dх;
·х²dх;
12. ∫ 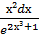 ;
;
13. ∫  ·х²dх;
·х²dх;
14. ∫соs(2 – 3х)dх;
15. 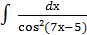
Практическая работа № 7
по дисциплине «Математика»
по теме: «Нахождение неопределенных интегралов методом введения новой переменной»
для специальностей 134702, 080110. 2 курс.
Вариант 4.
Найти неопределенные интегралы методом подстановки:
1. ∫(4х² + 3)⁵·хdх;
2. ∫(5х³ - 4)⁶ ·х²dх;
3. ∫ 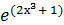 ·х²dх;
·х²dх;
4. ∫ 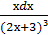 ;
;
5. ∫соs(5 - х²)·хdх;
6. ∫ 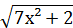 · хdх;
· хdх;
7. ∫(3х – 5)⁴dх;
8. ∫  ;
;
9. ∫ 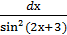 ;
;
10. ∫  ;
;
11. ∫  dх;
dх;
12. ∫  ;
;
13. ∫ 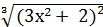 ·хdх;
·хdх;
14. ∫х⁵ соsх⁶dх;
15. ∫соs  dх
dх
Составила преподаватель Чуфенёва Н.И.
Практическая работа № 8
по дисциплине «Математика»
по теме: «Нахождение неопределенных интегралов методом интегрирования «по частям»
для специальностей 134702, 080110. 2 курс.
Вопросы для повторения:
1. Сформулируйте определение первообразной.
2. Дайте определение неопределенного интеграла.
3. Сформулируйте свойства неопределенного интеграла.
4. Какая формула применяется в методе интегрирования «по частям?»
Вариант 1.
Найдите неопределенные интегралы методом
интегрирования «по частям»:
1. ∫lnх dх;
2. ∫аrctgх dх;
3. ∫(х+1) 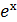 dх;
dх;
4. ∫ х² sinх dх.
5. ∫ х² 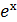 dх
dх
Практическая работа № 8
по дисциплине «Математика»
по теме: «Нахождение неопределенных интегралов методом интегрирования «по частям»
для специальностей 134702, 080110. 2 курс.
Вопросы для повторения:
1. Сформулируйте определение первообразной.
2. Дайте определение неопределенного интеграла.
3. Сформулируйте свойства неопределенного интеграла.
4. Какая формула применяется в методе интегрирования «по частям?»
Вариант 2.
Найдите неопределенные интегралы методом
интегрирования «по частям»:
1.  dх;
dх;
2. ∫ аrcsinх dх;
3. ∫ 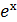 sinх dх;
sinх dх;
4. ∫ х² соsх dх;
5. ∫ (х – 1) 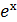 dх
dх
Практическая работа № 9
по дисциплине «Математика»
по теме: «Формулы прямоугольников. Формула трапеций. Формула Симпсона. Абсолютная погрешность при численном интегрировании».
для специальностей 134702, 080110. 2 курс.
Задание. Найдите по формулам прямоугольников, трапеций, Симпсона определённый интеграл.
Вариант 1 
Вариант 2 
Вариант 3 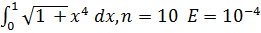
Вариант 4 
Вариант 5 
Вариант 6 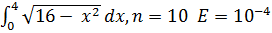
Вариант 7 
Вариант 8 
Практическая работа № 10
по дисциплине «Математика»
по теме: «Решение задач на определение различных величин
с помощью определенного интеграла»
для специальностей 134702, 080110. 2 курс.
Вариант 1.
1. Вычислить площадь фигуры ограниченной линиями:
а) у = х + 2; у = 0; х = 3;
б) у = -х ² + 5; у = х + 3;
в) у = sin2х; х = -  ; х =
; х = 
г) у =  ; х = 1; х = 3; у = 0.
; х = 1; х = 3; у = 0.
2. Вычислить путь, пройденный материальной точкой за третью секунду движения, если точка движется прямолинейно по со скоростью:
υ = (3 t + t²) м /с.
Практическая работа № 10
по дисциплине «Математика»
по теме: «Решение задач на определение различных величин с помощью определенного интеграла»
для специальностей 134702, 080110. 2 курс.
Вариант 2.
1. Вычислить площадь фигуры, ограниченной линиями:
а) у = -х + 2; у = 0; х = -3;
б) у = х²; у = х + 2;
в) у = соsх; х = -  х =
х =  ;
;
г) у = 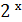 ; у = 0; х = - 1; х = 2.
; у = 0; х = - 1; х = 2.
2. Вычислить высоту подъёма материальной точки, брошенной с поверхности земли, если скорость движения выражается формулой:
υ = (29, 4 – 9,8t) м /с.
Практическая работа № 10
по дисциплине «Математика»
по теме: «Решение задач на определение различных величин с помощью определенного интеграла»
для специальностей 134702, 080110. 2 курс.
Вариант 3.
1. Вычислить площадь фигуры, ограниченной линиями:
а) у = х + 3; у = 0; х = 2;
б) у = х² + 1; у = 2х + 4;
в) у = 2 соs х; х = -  ; х =
; х =  ;
;
г) у =  ; у = 0; х = 1; х = 3.
; у = 0; х = 1; х = 3.
2. Вычислить путь, пройденный материальной точкой за три секунды от начала движения, если точка движется прямолинейно со скоростью:
υ = (2t² - t) м /с.
Практическая работа № 10
по дисциплине «Математика»
по теме: «Решение задач на определение различных величин с помощью определенного интеграла»
для специальностей 134702, 080110. 2 курс.
Вариант 4.
1. Вычислить площадь фигуры, ограниченной линиями:
а) у = - х + 3; у = 0; х = - 1;
б) у = х² - 4; у = 2х – 1;
в) у = 2 sin х; х = -  ; х =
; х =  ;
;
г) у = 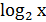 ; у = 0; х = 1; х = 4.
; у = 0; х = 1; х = 4.
2. Вычислить путь, пройденный материальной точкой за пятую секунду движения, если точка движется прямолинейно со скоростью:
υ = (3t² + t) м /с.
Практическая работа №10
по дисциплине «Математика»
по теме: «Решение задач на определение различных величин с помощью определенного интеграла»
для специальностей 134702, 080110. 2 курс.
Вариант 5.
1. Вычислить площадь фигуры, ограниченной линиями:
а) у = -х + 5; у = 0; х = -1;
б) у = х²; у = 4;
в) у = sin3х; х = -  ; х =
; х =  ;
;
г) у = ln х; х = 1; х = e.
2. Вычислить путь, пройденный материальной точкой за три секунды от начала движения, если точка движется прямолинейно со скоростью:
υ = (3t² - t³) м /с.
Практическая работа №10
по дисциплине «Математика»
По теме: «Решение задач на определение различных величин с помощью определенного интеграла»
для специальностей 134702, 080110. 2 курс.
Вариант 6.
1. Вычислить площадь фигуры, ограниченной линиями:
а) у = х + 5; у = 0; х = 1;
б) у = х² - 4; у = 0;
в) у = cоs3х; х = -  ; х =
; х =  ;
;
г) у =  ; х = 0; х = 1.
; х = 0; х = 1.
2. Вычислить высоту подъёма тела, брошенного с поверхности земли, если скорость движения выражается формулой:
υ = (49 – 9,8 t) м /с.
Практическая работа № 10
по дисциплине «Математика»
по теме: «Решение несложных задач на определение различных величин с помощью определенных интегралов»
для специальностей 134702, 080110. 2 курс.
Вариант 7.
1. Найдите площадь фигуры, ограниченной линиями:
а) 
б) 
в) 
г) у = ln х; х = 1; х = 2.
2. Скорость движения точки 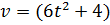 м/с. Найдите путь, пройденный точкой за 5 с от начала движения.
м/с. Найдите путь, пройденный точкой за 5 с от начала движения.
3. функции:
6) у = 3х – 4;
7) у = - х² + 2х + 3;
8) у = х³ - 3х² + 2;
9) у =  ;
;
Практическая работа № 10
по дисциплине «Математика»
по теме: «Решение несложных задач на определение различных величин с помощью определенных интегралов»
для специальностей 134702, 080110. 2 курс.
Вариант 8.
1. Найдите площадь фигуры, ограниченной линиями:
а) 
б) 
в) 
г) у = 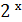 ; х = 0; х = 1.
; х = 0; х = 1.
2. Скорость движения точки  м/с. Найдите её путь за вторую секунду.
м/с. Найдите её путь за вторую секунду.
3. функции:
6) у = - 7х + 5;
7) у = 2х² + 4х – 3;
8) у = 3х³ - 3х² + 1;
9) =  ;
;
10) у =  .
.






