ƒл€ того чтобы по части €влени€ можно было судить о €влении в целом, о его закономерност€х, необходима оценка достоверности результатов исследовани€. ћерой достоверности показател€ €вл€етс€ его ошибка - ошибка представительности (репрезентативности). ќшибка показывает насколько результат, полученный при выборочном исследовании, отличаетс€ от результата, который мог бы быть получен при сплошном исследовании всей генеральной совокупности. —редн€€ ошибка средней арифметической (mћ) или средн€€ ошибка относительной величины (mр). –ассчитываетс€ по формуле: при n 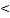 30
30
MM = 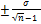 ; Mp=
; Mp= 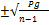 , где –- величина показател€, дл€ которого определ€етс€ ћр,а g= 100%-–% (если показатель определ€етс€ в процентах) или 1000% - –%о (если показатель определ€етс€ в промилле)
, где –- величина показател€, дл€ которого определ€етс€ ћр,а g= 100%-–% (если показатель определ€етс€ в процентах) или 1000% - –%о (если показатель определ€етс€ в промилле)
ѕри n 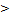 30 MM =
30 MM =  ; Mp=
; Mp= 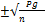
”меньшить ошибку можно увеличив число наблюдений (n)
ќценить достоверность результатов исследовани€ Ч значит, установить веро€тность прогноза, с которой результаты исследовани€ на основе выборочной совокупности можно перенести на генеральную совокупность или другие исследовани€. ќшибка представительности (репрезентативности) позвол€ет определить пределы, в которых с соответствующей степенью веро€тности безошибочного прогноза находитс€ истинное значение искомого параметра, т.е. доверительные границы. Pген = Pвыб ± tm (дл€ относительных показателей), ћген = ћвыб ± tm (дл€ средних величин), где –ген и ћген - искомые генеральные параметры частоты и среднего уровн€, –выб и ћвыб Ц найденные выборочные показатели, m Ц ошибка представительности, t Ц доверительный критерий. ќпределенной степени веро€тности безошибочного прогноза соответствует константное значение доверительного критери€, величина которого определ€етс€ по таблице интеграла веро€тностей (при n>30, приложение, табл. 1) или по таблице критери€ t (при n<30, приложение, табл. 2). ѕри использовании таблицы критери€ t число степеней свободы дл€ доверительных границ составл€ет n -1. ¬ медико-социальных исследовани€х минимальной достаточной веро€тностью безошибочного прогноза €вл€етс€ 95% (Pt =0,95), что допускает веро€тность ошибки р = 0,05. ¬ наиболее ответственных случа€х, когда необходимо сделать особенно важные выводы, веро€тность безошибочного прогноза возрастает до 99% (Pt =0,99, или р = 0,01) и даже до 99,9% (Pt =0,999, р = 0,001). ƒоверительные границы используютс€ не только дл€ оценки достоверности выборочного результата, но и при планировании в здравоохранении.
Ќаиболее распространенным методом оценки достоверности разности между сравниваемыми выборочными результатами €вл€етс€ критерий —тьюдента, предложенный ¬. √оссетом. ритерий t позвол€ет производить сравнение только между двум€ выборочными величинами. ≈сли необходимо сравнить между собой несколько однородных выборочных величин, то они сравниваютс€ поочередно. ритерий достоверности (—тьюдента) определ€етс€ как величина разности средних величин или относительных показателей, деленна€ на извлеченную из квадратного корн€ сумму квадратов ошибок средних арифметических или относительных показателей. t = 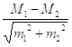 и t=
и t= 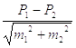
–азница между сравниваемыми выборочными величинами существенна и статистически достоверна при веро€тности безошибочного прогноза 95%, т.е. величина критери€ —тьюдента должна быть равна или больше 2 (при n >30). “олько при этих услови€х прогноз считаетс€ безошибочным, свидетельствующим о надежности используемого нового метода (лекарственного препарата, гигиенических характеристик).






