Классификация грамматик. Иерархия Хомского.

Ограничение типов правил, которые могут появляться в грамматике позволяет определить ряд специальных классов грамматик. Одна из стандартных классификаций известна как иерархия Хомского. Ее описывают следующим образом: 1. Любая грамматика определенного ранее вида – грамматика типа 0. 2. Если для всех правил вида α → β, |α| ≤ |β|, где |α| и |β| – длина, т.е. число символов соответственно α и β, то грамматика называется грамматикой типа 1, или контекстно-зависимой (КЗ). 3. Если все левые части правил грамматики состоят из одного нетерминального символа, то это грамматика типа 2, или контекстносвободная (КС). 4. Грамматика называется грамматикой типа 3, или регулярной, если каждое правило грамматики имеют одну из следующих форм. В случае грамматики, выровненной вправо, в правой части грамматики имеется не более одного нетерминала, который может быть только самым правым символом: A → a A → aB B случае грамматики, выровненной влево, в правой части грамматики имеется не более одного нетерминала, который может быть только самым левым символом: A → a A → Ba Иерархия – включающая, т.е. все грамматики типа 3 являются грамматиками типа 2 и т.д. Иерархия грамматик соответствует иерархии языков. Например, если язык можно генерировать с помощью грамматики типа 2, то его называют языком типа 2. Необходимо помнить, что если для генерации языка можно использовать несколько грамматик, то тип языка соответствует грамматике с наибольшим типом. Иерархия Хомского важна с точки зрения построения трансляторов с различных языков. Чем меньше ограничений в грамматике, тем сложнее ограничения, которые можно наложить на генерируемый язык. Чем более универсален класс используемой грамматики, тем больше свойств языка мы можем описать. Однако чем более универсальна грамматика, тем сложнее должна быть программа, распознающая строки соответствующего языка. Грамматики типа 3 можно использовать для описания некоторых свойств языков программирования или высокоуровневых языков описания аппаратуры. Например, для генерирования идентификаторов по определению многих языков программирования можно воспользоваться следующими правилами: I → l I → l R R → l R → d R → l R R → d R где буква (l) и цифра (d) обозначают терминалы (для краткости будем считать так, потому что перечисление всех возможных букв и цифр потребовало бы написания слишком большого числа правил).

Иногда удобно объединять правые части правил, имеющих одинаковые левые части. Вышеприведенную грамматику можно также записать в виде: I → l | l R R → l | d | l R | d R Вертикальную черту здесь надо понимать как "или". Многие "локальные" средства языков программирования, например константы, ключевые слова языка и строки, представляются с помощью грамматик типа 3. Некоторые очень простые языки описания аппаратуры также можно описать с помощью регулярной грамматики. Однако грамматики типа 3 генерируют только строго ограниченные типы языков – регулярные выражения.

В алфавите А к регулярным выражениям относятся следующие: 1. Элемент А (или пустая строка). Если P и Q – регулярные выражения, то регулярными будут также и выражения 2. PQ (Q следует за P) 3. P | Q (P или Q) 4. P* (нуль или более экземпляров P) В алфавите {a, b, c} ab* | ca* – регулярное выражение, которое описывает язык, включающий следующие строки (помимо прочих): abb c caaa ab ca Пример регулярного выражения. Регулярное выражение, описывающее идентификатор, имеет вид: L (L | D)*, где L обозначает букву, D – цифру. У регулярных выражений есть существенные ограничения. Например, регулярное выражение не может задавать шаблоны скобок произвольной длины, и, следовательно, их нельзя генерировать с помощью грамматики типа 3. Пример нерегулярного выражения. Рассмотрим язык, состоящий из строк открывающих и закрывающих скобок (плюс пустая строка), обладающих следующими свойствами: 1.) При чтении слева направо число встреченных закрывающих скобок никогда не превышает число встреченных открывающих скобок. 2.) В каждой строке содержится одинаковое число открывающих и закрывающих скобок. Например, следующие строки принадлежат языку: () (() () (())) (() () (() (()))) (()) а приводимые ниже – нет: ((() ()) – не соответствует правилу 2.

())) ((() – не соответствует правилу 1. Не существует способа представления этого языка с помощью регулярного выражения или его генерирования с помощью грамматики типа 3. Однако этот язык генерируется следующей контекстно-свободной грамматикой: S → (S) S → SS S → ε В большинстве языков программирования и языков описания аппаратуры имеются пары скобок, которые необходимо согласовывать, например: (), [ ], begin end каждой открывающей скобке должна соответствовать закрывающая. Так begin () end – правильно begin (end) – неправильно Контекстно-свободная грамматика позволяет специфицировать подобные ограничения. Как правило, большая часть синтаксиса языков программирования и специализированных языков САПР описывается с помощью КС-грамматики. Однако у большинства языков есть некоторые свойства, которые нельзя выразить с помощью КС-грамматики. Например, присваивание X:=Y может быть допустимым, если объявлено, что X и Y имеют соответствующие типы, или недопустимым при несоответствии типов. Условие такого вида не может быть специфицировано КСграмматикой, и компиляторы обычно выполняют проверку типа не на фазе формального синтаксического анализа. Однако идею КС-грамматики можно расширить, включив некоторые контекстно-зависимые свойства языков. Двухуровневые грамматики (W-грамматики, названной так в честь их изобретателя – А. ван Вейнгаардена). Идея применения двухуровневой грамматики состоит в том, что если правила обычной грамматики обеспечивают конечный способ описания языка, состоящего из бесконечного числа строк, то здесь вторая грамматика применяется для генерирования бесконечного числа правил, которые в свою очередь генерируют предложения языка. Применение второй грамматики позволяет избежать рутинной работы, связанной с написанием бесконечного числа порождающих правил. С помощью двухуровневой грамматики можно генерировать любой язык типа 0. Данная концепция является даже слишком мощной (КЗ свойства большинства машинных языков относительно просты). Атрибутивные грамматики. Атрибуты применяются для описания КЗ (точнее К-несвободных) аспектов языка. Рассмотрим пример. Пусть в некотором языке идентификаторы могут иметь тип int или char и являются терминалами грамматики. Описание с помощью КС порождающих правил. D → int I D → char I Описав идентификатор, мы хотим запомнить его тип. Этот тип будет свойством описания, видоизменим грамматику, чтобы это указать: D (.ID, MODE) → int (.MODE1) I(.ID1) ID = ID1 MODE = MODE1 аналогично для char. MODE, MODE1, ID, ID1 пишутся в скобках после терминала или нетерминала грамматики и представляют собой его признаки (атрибуты). Преимущество атрибутивных грамматик в том, что они выглядят как КС, но могут специфицировать КЗ конструкции языка. Фактически любой язык типа 0 можно описать с помощью атрибутивной грамматики. Так как языки программирования представляется как КС, к которым добавляются контекстные ограничения, атрибутивные грамматики хорошо подходят для их описания.

Пример регулярного выражения. Регулярное выражение, описывающее идентификатор, имеет вид: L (L | D)*, где L обозначает букву, D – цифру. У регулярных выражений есть существенные ограничения. Например, регулярное выражение не может задавать шаблоны скобок произвольной длины, и, следовательно, их нельзя генерировать с помощью грамматики типа 3.

Пример нерегулярного выражения. Рассмотрим язык, состоящий из строк открывающих и закрывающих скобок (плюс пустая строка), обладающих следующими свойствами: 1.) При чтении слева направо число встреченных закрывающих скобок никогда не превышает число встреченных открывающих скобок. 2.) В каждой строке содержится одинаковое число открывающих и закрывающих скобок. Например, следующие строки принадлежат языку: () (() () (())) (() () (() (()))) (()) а приводимые ниже – нет: ((() ()) – не соответствует правилу 2.

23 ())) ((() – не соответствует правилу 1. Не существует способа представления этого языка с помощью регулярного выражения или его генерирования с помощью грамматики типа 3. Однако этот язык генерируется следующей контекстно-свободной грамматикой: S → (S) S → SS S → ε В большинстве языков программирования и языков описания аппаратуры имеются пары скобок, которые необходимо согласовывать, например: (), [ ], begin end каждой открывающей скобке должна соответствовать закрывающая. Так begin () end – правильно begin (end) – неправильно Контекстно-свободная грамматика позволяет специфицировать подобные ограничения. Как правило, большая часть синтаксиса языков программирования и специализированных языков САПР описывается с помощью КС-грамматики. Однако у большинства языков есть некоторые свойства, которые нельзя выразить с помощью КС-грамматики. Например, присваивание X:=Y может быть допустимым, если объявлено, что X и Y имеют соответствующие типы, или недопустимым при несоответствии типов. Условие такого вида не может быть специфицировано КСграмматикой, и компиляторы обычно выполняют проверку типа не на фазе формального синтаксического анализа. Однако идею КС-грамматики можно расширить, включив некоторые контекстно-зависимые свойства языков.

Модели задания языков

Нотация Бэкуса-Наура. Для формального задания различных грамматик формальных языков также необходим язык. Такой язык называется метаязыком. Исторически первым метаязыком является нотация Бэкуса-Наура, или БНФнотация, которая названа так в честь Дж.Бэкуса (который был главным разработчиком первого компилятора для языка Фортран) и Питера Наура (который играл основную роль в разработке одного из первых алгоритмических языков – Алгола-60). Эта нотация, использованная впервые для строгого определения Алгола-60, была предшественницей правил порождающей КС-грамматики Хомского. Нетерминалы здесь помещаются в угловые скобки, символ '::=' используется вместо стрелки "→". Именно здесь было использовано упрощение, при котором альтернативы одного и того же нетерминала записываются в правой части одного правила через знак '|', имеющий смысл "либо". Расширенная БНФ-нотация включает две конструкции, полезные при спецификации практических языков программирования. Первая с помощью фигурных скобок позволяет легко описать повторение 0 или произвольное число раз некоторой цепочки. Например, синтаксис Турбо-Паскаля (1985 г.) описывает структуру описаний переменных так: <variable-declaration-part>::=var <variable-declaration> {; <variable-declaration>} При замене нетерминала левой части продукции содержимое фигурных скобок может повторяться произвольное число раз, в том числе и ни разу. Это, очевидно, похоже на операцию итерации Клини для регулярных множеств, что можно, конечно, представить так: {β} в БНФ эквивалентно (β)* в регулярных выражениях. В общем, продукция БНФ А::=α{β}γ эквивалентна трем продукциям: А→αВγ, В→Вβ и В→ε в стандартной записи грамматик Хомского. Вторая конструкция с помощью квадратных скобок определяет опцию – необязательный элемент. Например, целая константа может быть описана как: <integer-constant>::= [ + | - ] <digit> {<digit>} Эта спецификация задает возможность отсутствия знака перед целой константой, представляющей собой цепочку из одной или более цифр. В общем, продукция БНФ А::=α[β]γ эквивалентна двум продукциям: грамматики Хомского А→αβγ и А→αγ.

Часто нетерминалы в БНФ не выделяются никак, в то время как терминалы явно выделяются парой апострофов, а вместо символа '::=' используется просто '=': ident = letter { letter | digit } integer-constant =[ '+' | '-' ] digit { digit } Итак, БНФ-нотация – это просто удобная форма записи правил КС-грамматик Хомского как регулярных выражений (а не цепочек символов). Очевидно, что такое обобщение не выводит грамматику из класса КС-грамматик. Язык, который может быть специфицирован одним регулярным выражением, может быть представлен одним выражением в БНФ-нотации или же грамматикой типа 3 (автоматной грамматикой).

 

Язык синтаксических диаграмм Синтаксические диаграммы служат для определения языков с помощью графического представления. Они были использованы для задания синтаксиса языков Паскаль, Модула-2 и Фортран 77. Синтаксические диаграммы являются порождающим механизмом. Правила порождения цепочек языка представлены в виде нескольких графов потоков данных с одним входом и одним выходом. Любой путь в диаграмме от входа к выходу задает возможную последовательность символов в порождаемой цепочке языка. Каждому нетерминалу соответствует своя диаграмма. Встречающиеся нетерминалы должны быть заменены произвольной цепочкой, определяемой диаграммой, помеченной этим нетерминалом. Например, идентификатор в этой нотации может определяться так:

 

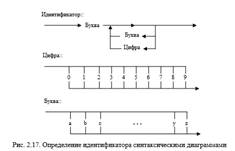
Покажем, что синтаксические диаграммы равномощны классу КС-грамматик Хомского. Иными словами, докажем, что класс языков, порождаемых синтаксическими диаграммами, совпадает с классом КС-языков. Очевидно, что любая КС-грамматика может быть представлена эквивалентным набором синтаксических диаграмм. Действительно, сопоставим каждому множеству правил КС-грамматики G с одним и тем же нетерминалом в левой части вида A→α1α2…αn одну синтаксическую диаграмму с n разветвлениями, по одному для каждой альтернативы нетерминала А.

Очевидно, что так определенное множество синтаксических диаграмм порождает тот же язык, что и грамматика G.

 

Грамматики с рассеянным контекстом Этот класс порождающих грамматик предложен известными исследователями в области формальных языков Шейлой Грейбах и Дж. Хопкрофтом [ГХ75]. Грамматики с рассеянным контекстом являются обобщением грамматик Хомского, цель их введения– упростить описание контекстных свойств естественных и искусственных языков (в частности, языков программирования). Авторы обосновывают необходимость введения такого расширения грамматик Хомского следующим. Контекстно-свободные грамматики Хомского слишком слабы, чтобы описать такие свойства языков программирования, как запрет использования неописанной переменной, согласование типов в операторе присваивания и т.п., поскольку для спецификации подобных контекстные свойств необходимо передавать информацию между произвольно далеко отстоящими частями предложения. Например, язык { wcww∈{0,1}*}, абстрагирующий проблему декларации переменных до их использования, не контекстно-свободный. Другим примером служит контекстно-зависимый язык L={anbmcndmm,n≥1}. Он абстрагирует проблему проверки того, что число формальных параметров в декларации процедуры равно числу фактических параметров в вызове этой процедуры, если интерпретировать an и bm как списки формальных параметров в декларациях двух процедур с n и m аргументами, а cn и dm как списки фактических параметров в вызовах этих процедур ([ASU86], стр.178). Контекстно-зависимые грамматики, которые могут порождать подобные языки, неудобны для практического применения, они плохо приспособлены для приписывания смысла предложениям. Для того, чтобы передавать информацию между далеко отстоящими частями предложения без передвижения нетерминальных символов, понятие контекстной замены, предложенной в грамматиках типа 1 Хомского следует обобщить так, чтобы замена символа зависела от контекста, но нетерминал мог бы быть заменен даже если контекст не смежен с ним. Так возникла идея грамматик с рассеянным контекстом. Определение 2.7. Порождающей грамматикой с рассеянным контекстом называется четверка объектов: G=(T,N,S,Р), где: T – конечное непустое множество (терминальный словарь); N - конечное непустое множество (нетерминальный словарь); S – начальный символ - S∈N; Р – конечное непустое множество правил (продукций), каждое из которых имеет вид (А1,..., Аn)→ (w1,...,wn), n≥1, где Аi∈N, и wi∈(TUN)+. Грамматика с рассеянным контекстом, в отличие от грамматики Хомского, имеет в качестве продукций пары векторов, один из которых – заменяемые символы – это только нетерминалы, а другой – соответствующее количество непустых цепочек объединенного словаря. Отношение '⇒' непосредственной выводимости на множестве цепочек в грамматиках с рассеянным контекстом определяется так: Пусть (А1,..., Аn)→ (w1,...,wn)∈Р и хi∈ (T∪N)*. Тогда: х1А1... хnAnxn+1 ⇒ х1 w1... хn wn xn+1. Таким образом, сразу несколько нетерминалов, стоящих произвольно далеко в порождаемой цепочке, могут быть заменены одновременно на соответствующие им цепочки объединенного словаря. Пусть ' ⇒*' означает рефлексивное и транзитивное замыкание отношения ' ⇒'. Определим язык, порождаемый грамматикой G, как множество L(G)={w∈T+S⇒* w}.

 

Трансформационные грамматики НС-грамматики (грамматики типа 1) и грамматики типа 0 достаточно точно могут описать простые фразы естественного языка. Однако, в применении к естественным языкам выявилось следующее ограничение, присущее всем порождающим грамматикам Хомского. Они порождают фразы языка синтаксически, безотносительно к семантике этих фраз, и не имеют каких-либо механизмов преобразования готовых фраз языка в различные формы с учетом их смысла. Речь идет о таком феномене естественных языков, как существование в нем правил преобразования (трансформации) предложений из повествовательной в вопросительную и отрицательную форму, или из активной в пассивную форму, причем с сохранением информации, содержащейся в исходной цепочке языка. В естественных языках такие трансформации обычны. Релевантная порождающая грамматика естественных языков должна иметь соответствующие механизмы, которых, очевидно, нет в грамматиках Хомского. Хомский ставил своей целью построение порождающего механизма именно для естественных языков, поэтому он продолжал развивать свою теорию порождающих грамматик дальше, с целью построенияь адекватных механизмов таких трансформаций. Эта новая модель получила название трансформационных грамматик. Трансформационные грамматики построены в предположении о том, что порождение человеком предложения осуществляется в два этапа. На первом с помощью правил так называемой "базовой" КСграмматики порождается относительно простая синтаксическая структура декларативного (повествовательного) предложения, которая называется "глубинной". Глубинная структура представляется в виде дерева вывода, которое называется "С-маркером". С-маркер не содержит терминальных символов. На втором этапе глубинная декларативная структура путем последовательного применения трансформационных правил превращается в более сложную синтаксическую структуру, в частности, вопросительную или отрицательную форму с сохранением информационной сути предложения. Такая структура называется поверхностной. Именно поверхностная структура состоит из терминальных символов и соответствует конкретному предложению. Таким образом, трансформационная часть грамматики (или Т-компонента) преобразует С-маркеры в поверхностную структуру предложения, которая включает терминалы, т.е. слова (словоформы) естественного языка. Распознавание предложений языков, порожденных трансформационными грамматиками связано с рядом трудностей. Такие распознаватели могут работать только на основе метода проб и ошибок, являются очень медленными, их алгоритмы имеют экспоненциальную сложность. В связи с этим в настоящее время для задания и распознавания естественных языков часто используются другие механизмы.

 

Языки сетей Петри Грамматики Хомского являются моделью, которая лежит в основе подавляющего большинства идей в области спецификации формальных языков. В частности, нотация Бэкуса-Наура является просто более удобным представлением правил грамматик Хомского типа 2, синтаксические диаграммы – их наглядным графическим представлением, а грамматики с рассеянным контекстом разрешают векторную замену сразу нескольких нетерминалов в порождаемой строке, что является простым обобщением КС-грамматик. Но грамматики Хомского отнюдь не единственно возможный способ задания языков. Фактически, порождающим механизмом при задании языка может служить формальная модель любой природы, какимто образом определяющая множество последовательностей объектов (символов) над конечным словарем. В этом разделе мы рассмотрим одну из таких моделей порождения - сети Петри.

Сети Петри используются для моделирования систем параллельных процессов. События, которые могут произойти в системе, представляются в сети Петри переходами. Множество возможных последовательностей срабатываний переходов характеризует ту систему, которая моделируется сетью Петри. Пометим некоторые (существенные для конкретного приложения) переходы сети символами конечного алфавита. Множество всех последовательностей пометок срабатываний переходов сети является, очевидно, языком, который называется свободным префиксным языком сети Петри. Таким образом, язык может определить динамику сети Петри. На рис.2.19 представлена сеть Петри, моделирующая использование семафора для решения проблемы взаимного исключения двух параллельных процессов. Проблема заключается в том, чтобы синхронизировать два параллельных процесса (представленных здесь последовательностями мест <р0, р1, р2> и <р3, р4, р5>) таким образом, чтобы в своих критических интервалах, связанных, например, с использованием общего ресурса, оба процесса не могли бы находиться одновременно. Критические интервалы в процессах моделируются местами р2 и р5. События входа в критический интервал и выхода из него моделируются для двух процессов переходами t1, t2 в одном процессе, и t4, t5 во втором. Именно эти интересующие нас события помечены (t1, t2 помечены а и b, а t4, t5 помечены b и d)). Легко видеть, что язык, порождаемый этой сетью Петри - это префиксный язык, определяемый регулярным выражением (ab+cd)*. Простейший анализ этого языка показывает, что проблема взаимного исключения здесь решена корректно. Действительно, все цепочки языка удовлетворяют требованию взаимного исключения: если один процесс вошел в свой критический интервал, то другой не может войти в свой подобный интервал, пока первый не выйдет из своего, что в терминах языка представлено так: цепочки языка не содержат фрагментов ас и са. Таким образом, анализ корректности сети Петри проведен здесь с помощью порождаемого сетью языка. Кроме префиксных языков удобно рассматривать так называемые терминальные языки сетей Петри. Терминальным языком сети Петри называется множество цепочек пометок последовательностей срабатывания переходов сети, приводящих к некоторой финальной разметке сети. Возникает вопрос: какой порождающей мощностью обладают сети Петри, иными словами, какие языки могут ими порождаться? Оказывается, что языки, порождаемые сетями Петри, занимают промежуточное положение между автоматными языками и языками, порождаемыми неограниченными грамматиками Хомского (и, следовательно, распознаваемыми машинами Тьюринга). Действительно, частным случаем сетей Петри являются конечные автоматы. Следовательно, все автоматные языки порождаются сетями Петри. Из следующего примера видно, что сети Петри строго мощнее конечных автоматов.

Теорема 2.3. [К84]. Класс помеченных сетей Петри строго мощнее класса конечных автоматов, не сравним с классом магазинных автоматов и строго менее мощен, чем класс машин Тьюринга.

Проблема разбора. Пример.

Компилятор должен решить проблему проверки строк символов, чтобы определить, принадлежат ли они данному языку, и если да, то распознать структуру строк в терминах порождающих правил грамматики. Эта проблема известна как проблема разбора. Исследуем грамматику с порождающими правилами (E - начальный символ). 1. Е → Е + Т 2. Е → T 3. T → T * F 4. T → F

5. F → (Е) 6. F → x 7. F → y

Ясно, что строка (x + y) * x принадлежит данному языку. В частности, это можно вывести следующим образом (для каждого шага вывода указан номер применяемого правила): 2) E ⇒ T 3) ⇒ T * F 4) ⇒ F * F 5) ⇒ (E)* F 1) ⇒ (E + T) * F 2) ⇒ (T + T) * F

4) ⇒ (F + T) * F 6) ⇒ (x + T)*F 4) ⇒ (x + F) * F 7) ⇒ (x + y) * F 6) ⇒ (x + y) * x

Или же это можно вывести так: 2) E ⇒ T 3) ⇒ T * F 6) ⇒ T * x 4) ⇒ F * x 5) ⇒ (E) * x 1) ⇒ (E + T) * x 4) ⇒ (E + F) * x

7) ⇒ (E + y) * x 2) ⇒ (T + y) * x) ⇒ (F + y) * x 6) ⇒ (x + y) * x

На каждом этапе первого вывода самый левый нетерминал в сентенциальной форме замещался с помощью одного из порождающих правил грамматики. Поэтому данный вывод называется левосторонним. Второй вывод, на каждом этапе которого замещается самый правый нетерминал, называется правосторонним. Существуют также другие выводы, не являющиеся ни лево-, ни правосторонними, однако при реализации трансляторов они практически не используются. Левосторонний разбор предложения определяется как последовательность порождающих правил, применяемая для генерирования предложения посредством левостороннего вывода. В данном случае левосторонний разбор можно записать как 2,3,4,5,1,2,4,6,4,7,6. Правосторонний разбор предложения является обратной последовательностью порождающих правил, используемых для генерирования предложения посредством правостороннего вывода; например, в вышеприведенном случае правосторонний разбор запишется в виде 6,4,2,7,4,1,5,4,6,3,2. Обратный порядок последовательности порождающих правил связан с тем, что правосторонний разбор обычно ассоциируется с приведением предложения к начальному символу, а не с генерированием предложения из начального символа (см. ниже разбор снизу вверх). Заметим, что каждое порождающее правило используется в обоих выводах (или разборах) одинаковое число раз. Дерево разбора. Вывод может быть описан также в терминах построения дерева, известного как синтаксическое дерево (или дерево разбора). Проблему разбора можно свести к 1) нахождению левостороннего разбора; 2) нахождению правостороннего разбора; 3) построению синтаксического дерева. Неоднозначные грамматики. В большинстве случаев левосторонний и правосторонний разборы и синтаксическое дерево являются уникальными. Однако для грамматики с порождающими правилами: S → S+S | x предложение x + x + x имеет два синтаксических дерева (рис. 4.2) и два левосторонних (и правосторонних) разбора: S ⇒ S + S S ⇒S + S ⇒S + S + S ⇒x + S ⇒ x + S + S ⇒ x + S + S ⇒ x + x + S ⇒ x + x + S ⇒ x + x + x ⇒ x + x + x

Если какое-либо предложение, генерированное грамматикой, имеет более одного дерева разбора, о такой грамматике говорят, что она неоднозначна. Эквивалентное условие заключается в том, что предложение должно иметь более одного левостороннего или правостороннего разбора. Задача установления неоднозначности грамматики является, в общем случае, неразрешимой, т.е. не существует универсального алгоритма, который принимал бы на входе любую грамматику и определял бы, однозначна она или нет. Некоторые неоднозначные грамматики можно преобразовать в однозначные, генерирующие тот же язык. Например, грамматика с порождающими правилами S → x | S + x является однозначной и генерирует тот же язык, что и рассмотренная ранее неоднозначная грамматика. Методы разбора обычно бывают нисходящими, т.е. начинают с начального символа и идут к предложению, или восходящими, т.е. начинают с предложения и идут к начальному символу. Отказ от решения в разборе называют возвратом. Методы разбора могут быть недетерминированными и детерминированными в зависимости от того, возможен возврат или нет. Недетерминированные методы разбора весьма дорогие с точки зрения памяти и времени и крайне затрудняют включение в синтаксический анализатор действий, выполняемых во время компиляции, результаты которых позднее должны быть аннулированы (например, построение таблицы символов и т.п.). В дальнейшем мы будем рассматривать лишь детерминированные методы разбора. Основное внимание в настоящем учебном пособии уделено методам нисходящего разбора, они же используются в лабораторных работах и при курсовом проектировании. Методы восходящего разбора рассмотрены в отдельной главе.

Лексический анализ.

Первой фазой процесса компиляции является лексический анализ, то есть группирование строк литер, обозначающих идентификаторы, константы или слова языка и т.д., в единые символы (лексемы). Этот процесс может идти параллельно с другими фазами компиляции (например, в однопроходных компиляторах). Однако, в любом случае, при описании конструкции компилятора и его построения удобно представлять лексический анализ как самостоятельную фазу. Блок сканирования (сканер) должен выдавать каждую лексему, устанавливая ее принадлежность тому или иному классу. Выбор классов зависит от особенностей транслируемого языка. Часто выделяют классы имен переменных, констант, ключевых слов, арифметических и логических операций ("+", "-", "*", "/" и т.д.), специальных символов ("=", ";" и т. д.). Характер распознаваемых строк может намного упростить процесс лексического анализа. Все эти строки можно генерировать с помощью регулярных выражений. Например, вещественные числа можно генерировать посредством регулярного выражения (+ | -) d d*.d*, где d обозначает любую цифру. Из выражения видно, что вещественное число состоит из следующих компонентов, расположенных именно в таком порядке: 1. возможного знака; 2. последовательности из одной или более цифр; 3. десятичной точки; 4. последовательности из нуля или более цифр.

Регулярные выражения эквивалентны грамматикам типа 3. Например, грамматика типа 3, соответствующая регулярному выражению для вещественного числа, имеет порождающие правила: R → +S | -S | dQ S → dQ Q → dQ |.F |. F → d | dF где R - начальный символ, d – цифра.

Существует полное соответствие между регулярными выражениями (а потому и грамматиками типа 3) и конечными автоматами, более подробно рассмотренными в следующей главе. Некоторые лексемы (например, *) могут быть распознаны по одному считанному символу, другие (такие, как:=) – по двум символам, а для идентификации третьих необходимо прочитать неизвестное заранее число символов (например, код константы). В последнем случае, чтобы найти конец лексемы, приходится считывать один лишний символ, не входящий в состав данной лексемы. Этот символ необходимо запоминать, чтобы при разборе следующей лексемы он не был утерян. Лексический анализатор, наряду с разбиением исходного потока символов на лексемы, может включать в исходный текст дополнительную информацию или исключать из него строки символов. Примером дополнительно включаемой информации являются номера строк. Если их не включить, то информация о том, в какой строке исходного текста находилась та или иная лексема, будет, в случае выполняющего сканирование в отдельном проходе компилятора, утеряна после лексического анализа. Однако для диагностики на фазе синтаксического анализа необходимо иметь возможность ссылаться на ошибки в программе с указанием номеров строк оригинального исходного текста. С другой стороны, комментарии включаются в текст программы или описания объекта проектирования только для предоставления человеку дополнительных пояснений. Они никак не влияют на генерируемый в дальнейшем код, и лексический анализатор обычно их просто исключает.