Приближенное вычисление интегралов
Приближённое вычисление определённого интеграла основано на геометрическом смысле интеграла и сводится к приближённому вычислению площади, ограниченной подынтегральной функцией f(x), прямыми x=a=x0, x=b=xn и осью OX (рис. 10.1).
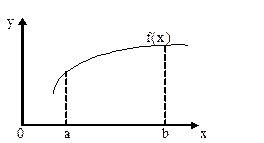Интервал [ a,b ] делится на n равных частей длиной 
.
Тогда значениям xi=xi-1+h, i=1,2...,n, соответствуют значения yi=f(xi).
Метод прямоугольников. В методе левых прямоугольников искомая площадь вычисляется как сумма площадей прямоугольников, основание которых равно h, а высота равна соответственно y0 для первого прямоугольника, y1 – для второго и т.д. вплоть до последнего с высотой yn-1. Тогда
Для метода правых прямоугольников аналогично
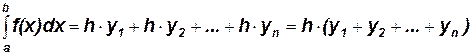
Метод трапеций. В методе трапеций определяется сумма площадей трапеций, основаниями которых являются ординаты y0, y1 и т.д., а высоты равны h.
Погрешность метода оценивается как 
, где М – максимальное значение второй производной f(x) на отрезке [a,b]. Используя это соотношение можно определить количество точек, на которое делится отрезок, исходя из заданной погрешности.
Чтобы вычислить определённый интеграл в приложении Mathcad нужно записать интеграл, подынтегральную функцию и пределы интегрирования. Например:
Для получения численного значения записывается выражение:
z=
Решение уравнений
Пусть имеется уравнение:
f(x)=0
Решение уравнения численными методами состоит из двух этапов: 1) отделение корней, т.е. нахождение таких отрезков [a,b] на оси OX, внутри которых имеется один корень; 2) вычисление корней с заданной точностью.
Одним из способов отделения корней является графический способ. Рассмотрим его на примере.
Пусть требуется отделить корни уравнения 3-x-ln(x)=0.
Перепишем исходное уравнение в виде 3-x=ln(x) и построим графики функций y=3-x и y=ln(x) (рис. 10.2). Из чертежа видно, что графики пересекаются в единственной точке, абсцисса которой находится внутри отрезка [1,3]. Знаки функции на концах отрезка разные: f(1)=3-1-ln(1)>0, f(3)=3-3-ln(3)<0. Значит, данное уравнение имеет действитель-ный корень, лежащий внутри отрезка [1,3], то есть а=1, в=3.
Можно также отделить корни, построив график функции в приложении Mathcad или в приложении Excel.
После того, как определен отрезок (или отрезки), внутри которого имеется один корень, можно вычислить его с заданной точностью одним из методов.
Решить уравнение с помощью Mathcad можно разными способами.
С помощью меню. Следует записать уравнение, в котором логический знак равенства (на экране он будет жирным) вводится при помощи панели Логический. Если уравнение приведено к виду f(x)=0, то можно ввести только левую часть уравнения без знака равенства и нуля.
Затем надо выделить в уравнении переменную, относительно которой оно решается, и выполнить Символика / Перемен-ная / Решение.
С помощью ключевого слова solve. Надо ввести уравнение и ключевое слово solve с панели Символика, в появившемся местозаполнителе записать имя переменной, относительно которой решается уравнение.
Для упрощения сложного решения можно после имени введенной переменной ввести ключевое слово simplify панели Символика. Ключевые слова при этом отобразятся записанными в столбик.
С помощью встроенной функции root. Следует задать начальное приближение корня и записать само уравнение:
x:=1
f(x):=3-x-ln(x)
Для получения значения корня нужно использовать встроенную функцию:
root(f(x),x)=
В приложении Excel можно составить программы по алгоритмам, приведенным выше, на языке VBA и произвести нужные вычисления.
Кроме того, для решения уравнения в приложении Excel имеется команда Подбор параметра в пункте меню Сервис. Чтобы решить уравнение надо на рабочем листе, например, в ячейке А1 записать начальное приближение корня, в ячейке В1 − записать само уравнение: =3-А1-Log(A1).
Выполнить Сервис/Подбор параметра. В появившемся окне задать следующие значения: в поле Установить в ячейке задать В1, в поле Значение − ввести 0, в поле Изменяя значение ячейки − А1. После нажатия ОК в ячейке А1 будет корень уравнения.
